Классификация точек разрывов графиков функций

Глава 3.

Занятие 6

Определения и свойства непрерывных функций.

 

Определение 6.1.Функцию 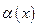назовём бесконечно малой (при ) если

(6.1)

Сокращённо это записывается так 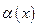( ) б.м.

Определение 6.2.Две б.м.называются эквивалентными если

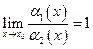(6.2)

Это записывается так .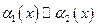

Основные свойства бесконечно малых.

Теорема 6.1.Пусть функции б.м., ограниченная функция, тогда справедливы следующие утверждения

1) также является б.м.( )

Сумма двух б.м. также б.м.

2) также является б.м.

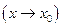
Произведение б.м. на ограниченную функцию также б.м.

 

3) Предел произведения переменных не изменится, если каждый б.м. сомножитель заменить эквивалентным б.м. сомножителем.

 

Пример 6.1. Пусть и предел существует, тогда

 

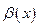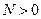Определение 6.3.Функцию назовем положительной бесконечно большой (б.б. при ) если для любого сколь угодно большого положительного числа все значения . Краткая запись будет выглядеть так .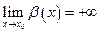

Определение 6.4.Функцию 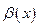назовем отрицательной бесконечно большой (б.б. при ) если для любого сколь угодно большого отрицательного числа все значения . Краткая запись будет выглядеть так .

Теорема6.2.Если 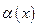положительная б.м. при , тогда есть положительная б.б. при .

Замечание. Положительную б.м. будем записывать так 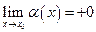. Тогда запись 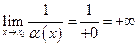будет означать, что величина есть положительная б.б.

Теорема6.3.Если 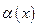отрицательная б.м. при , тогда есть отрицательная б.б. при .

Замечание. Отрицательную б.м. будем записывать так . Тогда запись будет означать, что величина есть отрицательная б.б.

 

При решении различного рода инженерных задач на практике широко используется класс функций, у которых значение функции в точке и предельное значение в этой же точке совпадают. Такие функции называются непрерывными.

 

Определение 6. 5. Функция называется непрерывной в точке тогда и только тогда если

(6.3)

 

Определение 6.6. Функция называется непрерывной на открытом интервале тогда и только тогда если она непрерывна в любой точке .

Теорема 6.4.Если функцию можно записать формулой

(6.4)

где б.м. ( ), то эта функция непрерывна в точке .

Доказательство.

Основные правила, применяемые к непрерывным функциям

ТЕОРЕМА6.5

Пусть функции и , непрерывны в точке 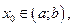тогда:

 

1) функции и также непрерывны в точке ;

2) функция также непрерывна в точке ;

3) функция также непрерывна в точке , если ;

 

4) Пусть функция непрерывна в точке , а функция

непрерывна в точке . тогда сложная функция непрерывна в точке

Доказательство. Если мы докажем для функции справедливость формулы (4) , то из результатов теоремы 6.4 будет следовать непрерывность функции в точке .

Пункты 1),2),3) теоремы 6.3 доказываются одинаково. Докажем, например, пункт 3)

Обозначим . По условию теоремы 6.3 и непрерывны в точке и .

Переходя к пределу при , по теореме о пределе дроби получаем

Следовательно, по определению 6.5 функция непрерывна в точке .

Пункт 3) доказан. Пункты 1), 2) доказываются аналогично.

Приведём схему доказательства четвёртого пункта. По условию теоремы функция непрерывна в точке . Тогда, если следует . В свою очередь функция непрерывна в точке и поэтому при 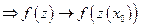. А это означает, что непрерывна в точке

 

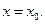
Из теоремы 3 следует очень полезная на практике теорема

 

ТЕОРЕМА 6.6. ЛЮБАЯ ЭЛЕМЕНТАРНАЯ ФУНКЦИЯ ЯВЛЯЕТСЯ НЕПРЕРЫВНОЙ В ОБЛАСТИ СВОЕГО ЕСТЕСТВЕННОГО ЗАДАНИЯ.

 

Напомним, что областью естественного задания функции называется наибольшее множество изменения аргумента , в котором можно вычислить значение данной функции.

Это означает, что все пункты теоремы 6.3 можно применять к любой элементарной функции.

 

Если функция задаётся без указания области задания, то это означает, что она задана на её естественном множестве задания.

Укажем ,например, естественные области задания функций

Ответами являются множества .

Если функция задаётся с указанием её области задания, то это означает, что её можно вычислить только для аргументов взятых из указанной области.
Например

Основные свойства непрерывных функций заданных на отрезке

Теорема 6.7.Пусть функция непрерывна на отрезке .Возьмём произвольное число : . Тогда всегда найдётся, по крайней мере, один аргумент 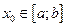такой, что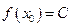

рис.1

Упражнение 6.1. Согласно результатам теоремы *7 порис.1 приближенно определить точки для данных С: С=0.2;С=0.3;С=1.

Теорема 6.8.Пусть функция непрерывна на отрезке , тогда найдутся аргументы функции такие, что для любых аргументов 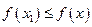и .

То есть у любой непрерывной на отрезке функции всегда найдётся наибольшее и наименьшее значение функции.

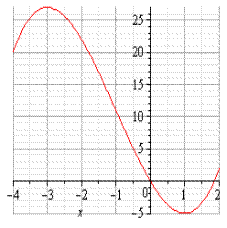
Рис.2

Упражнение 6.2.По рис.2 приближенно определить точки , в которых функция достигает наибольшего и наименьшего значений на отрезке . согласно результатам теоремы 6.8.

 

Классификация точек разрывов графиков функций

Функция непрерывна в точке тогда и только тогда, если выполняются равенства

(6.5)

Выполнение равенств (6.5) означает выполнение следующих условий

(6.6)