 |
Главная |
Правило исследования функции на непрерывность и на разрыв
|
из
5.00
|
При исследовании графика функции на разрыв всё зависит от того какое из условий (6.6)
нарушается.
I. Если нарушено условие A в (6.6), то абсциссу  можно назвать точкой неопределённости;
можно назвать точкой неопределённости;
II. Пусть условие А выполнено, но нарушено условие В. Тогда абсцисса  это точка
это точка
бесконечного разрыва графика функции;
Ш. Если условия А и В выполнены, а условие С нарушено, то абсцисса  является
является
точкой конечного разрыва графика функции; Такой разрыв графика называется
скачком;
IV. Пусть условия А, В и С выполнены, но нарушено условие D. Тогда точка  это
это
точка устранимого разрыва графика функции;
Иногда разрыв- скачок называют разрывом первого рода. Бесконечный разрыв называют разрывом второго рода.
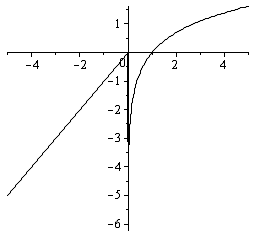

Рис.3а рис.3в
На рис.3а у графика в точке  бесконечный разрыв. На рис.3в у графика в точке
бесконечный разрыв. На рис.3в у графика в точке  разрыв -скачок.
разрыв -скачок.
Пример 6.2. Исследовать на непрерывность данные функции

Решение.1). Данная функция  является элементарной функцией (см. опр.1.9).
является элементарной функцией (см. опр.1.9).
Из теоремы 6.6 следует, что она непрерывна всюду в области своего задания  . Используя правило, исследуем её на непрерывность в точке
. Используя правило, исследуем её на непрерывность в точке 
Вычисляем левый предел  . При
. При  величина
величина  является отрицательной
является отрицательной
б.м. Следовательно, по теореме 6.3 величина  будет отрицательной б.б. при
будет отрицательной б.б. при  .
.
Откуда  .
.
Вычисляем правый предел  . При
. При  величина
величина  является положительной
является положительной
б.м. Следовательно, по теореме 6.2 величина  будет положительной б.б. при
будет положительной б.б. при  .
.
Откуда  .
.
Вывод. Функция  непрерывна всюду кроме точки
непрерывна всюду кроме точки  . В точке
. В точке  функция терпит разрыв второго рода (бесконечный разрыв).
функция терпит разрыв второго рода (бесконечный разрыв).
2). Данная функция  является элементарной функцией (см. опр.1.9).
является элементарной функцией (см. опр.1.9).
Из теоремы 6.6 следует, что она непрерывна всюду в области своего задания  . Используя правило, исследуем её на непрерывность в точке
. Используя правило, исследуем её на непрерывность в точке  .
.
Вычисляем левый предел  . При
. При 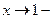 величина
величина  является положительной б.м. Следовательно, по теореме 6.2 величина
является положительной б.м. Следовательно, по теореме 6.2 величина  будет положительной б.б. при
будет положительной б.б. при 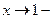 . Откуда
. Откуда  .
.
Вычисляем правый предел  . При
. При  величина
величина  является отрицательной б.м. Следовательно, по теореме 6.3 величина
является отрицательной б.м. Следовательно, по теореме 6.3 величина  будет отрицательной б.б. при
будет отрицательной б.б. при  . Откуда
. Откуда  .
.
Вывод. Функция  непрерывна всюду кроме точки
непрерывна всюду кроме точки  . В точке
. В точке  функция терпит разрыв второго рода (бесконечный разрыв).
функция терпит разрыв второго рода (бесконечный разрыв).
Пример 6.3. Исследовать данные функции на непрерывность и построить их графики



Решение. 1) На интервалах  функция непрерывна, так как на каждом она является элементарной функцией. Исследуем функцию в пограничных точках
функция непрерывна, так как на каждом она является элементарной функцией. Исследуем функцию в пограничных точках  и
и  . Для точки
. Для точки  имеем
имеем

Согласно правилу в точке  разрыв первого рода. Разрыв-скачок.
разрыв первого рода. Разрыв-скачок. 
Рис.4
Для точки  имеем
имеем 
Значение функции в точке 3равно 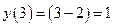 . Следовательно, в точке
. Следовательно, в точке  функция
функция
непрерывна. График функции приведён на рис.4.
2) На интервалах  функция непрерывна, так как на каждом она является элементарной функцией. Исследуем функцию в точках
функция непрерывна, так как на каждом она является элементарной функцией. Исследуем функцию в точках  и
и  .
.
Для точки  имеем
имеем

Согласно правилу в точке  разрыв первого рода. Разрыв-скачок.
разрыв первого рода. Разрыв-скачок.
Для точки  имеем
имеем

Значение функции в точке 2 равно  . Следовательно, в точке
. Следовательно, в точке  функция
функция
терпит разрыв. Разрыв-скачок. График функции приведён на рис.5.


Рис.5
|
из
5.00
|
Обсуждение в статье: Правило исследования функции на непрерывность и на разрыв |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

