Основные характеристики функций

Математический анализ функции одной переменной.

Основные определения.

Элементы теории множеств.

Множество – любая совокупность каких-либо предметов, называемых элементами множества. A-множество, a- элемент. aÎA. Множества конечные и бесконечные. Множество целых чисел бесконечно. Æ-пустое множество, не содержит элементов.

Объединением двух множеств А и В называется множество, элементами которого являются все элементы Аи В, одинаковые элементы включаются в множество один раз. Обозначение АÈВ.

Пересечение множеств А и В называют множество, элементы которого одновременно являются элементами А и В. АÇВ.

Если все элементы множества А являются элементами В, то А называют подмножеством В. АÌВ.

Числовые множества – элементы-числа (N,Z,R,Q-рациональные)

ЗНАЧКИ! $-существует, "-любой, каждый, всякий, :-такой, что, ]-пусть.

Числовой (действительной) осью называется прямая линия для точек которой следующим образом установлено взаимнооднозначное соответствия с числами: +

Точка О с нулем, указан единичный масштаб; для любого положительного числа а на оси соответствует единственная точка на оси, правее точки О, причём так, что расстояние от точки О до этой точки =а и число –а располагается симметрично точки О.

Число а, сопоставленное точке А на числовой оси, называют координатой точки А на числовой оси.

Интервалом на числовой оси называется множество таких действительных x, что a<x<b.

Полуинтервал-множество действительных чисел, для которых a£x<b/a<x£b.

Абсолютная величина числа.

Модулем |a| называется само а, если оно неотрицательно и –а, если а отрицательно.

Свойства модуля:

Для любого aÎR |a|³0(неотрицателен)

|a|=0 <=> a=0

-|a|£a£|a|

|a+-b|£|a|+|b|

|a+-b|³|a|-|b|

|ab|=|a||b|

e-окрестность точки х0, такие действительные х, для которых |х-х0|<e.

Проколотая окрестность – тот же интервал, за исключением точки х0.

Понятие функции.

Числовую величину х назовём переменной величиной, если она может принимать различные значения.

Х-множество всех значений х, XÎR.

Пусть существует множество YÎR. Если каждому х из Х по некоторому правилу сопоставлено единственное y из Y, то говорят, что на Х задана функция y=f(x) или

Функция определена, если заданы: множество Х(ОблОпредФункц), множество Y(МножЗначФункц), правило сопоставления элементов Y элементам Х.

Способы задания функций. Табличный, аналитический, графический, Описательный

Основные характеристики функций.

Функция y=f(x), определенная на множестве D, называется чётной, если для любого x из D, выполняется условие -xÎD, f(-x)=f(x). Функция y=f(x), определенная на множестве D, называется нечётной, если для любого x из D, выполняется условие -xÎD, f(-x)=-f(x).

Пусть функция y=f(x) определена на D и пусть D1cD(подмножество), тогда: 1)если для любых х1 и х2 ÎD1 выполняется x1<x2 => f(x1)<f(x2), то функция называется возрастающей на множестве D1. 2)Если для любых х1 и х2 ÎD1 выполняется x1<x2 => f(x1)£f(x2), то функция называется неубывающей на множестве D1. 3)Если для любых х1 и х2 ÎD1 выполняется x1<x2 => f(x1)>f(x2), то функция называется убывающей на множестве D1. 4)Если для любых х1 и х2 ÎD1 выполняется x1<x2 => f(x1)³f(x2), то функция называется невозрастающей на множестве D1. для случаев 1,2,3,4 функцию называют монотонной, для 1,3-строго монотонной.

1.5 Классификация функций

Простейшими элементарными функциями называют: постоянные функции f(x)=c, c=const. степенные, показательные, логарифмические, все тригонометрические и им обратные, все функции, полученные с помощью конечного числа арифметических действий над простыми элементарными функциями, а так же суперпозиции этих функций – составляют класс элементарных функций.

Классификация: P(x)=a0+a1x+a2x²+…+amx^m, m³0 – целая рациональная функция, или алгебраическое множество степени m. 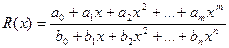, m³0,n³0 – дробно рациональная функция. Функция, полученная с помощью конечного числа суперпозиций и их арифметических действий над степенными функциями как с целым, так и с дробным показателем и не являющихся рациональными называют иррациональными. Все функции, не являющиеся рациональными или иррациональными называют трансцендентными(логарифм, показательная).