 |
Главная |
Производная по направлению и градиент
|
из
5.00
|
рассмотрим функцию Z=f(M) в точке М(х;у), функция определена в окрестности этой точки. Единичные вектор l={cosa;cosb}, где a и b - углы между вектором и осями. Для характеристики скорости изменения функции в точке М в направлении вектора l вводится понятие производной по направлению.
Через точку М(х;у) проводим прямую L , параллельную вектору l, на прямой возьмём точку М1 так. Чтобы направление вектора MM1 и вектора l совпадали. |MM1|=Dl, Dl=ÖDx2+Dy2. значит Z получит полное приращение DZ=f(x+Dx;y+Dy)-f(x;y). Предел отношения DZ к Dl при стремлении Dl к нулю называется производной функции Z в точке М по направлению вектора l. 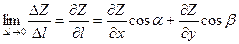 .
.
Определение: Градиентом функции Z=f(M) в точке М(х;у) называется вектор, координаты которого равны частным производным в точке М. gradZ={Zx’(M);Zy’(M)}.
Замечание: используя обозначение градиента производная по направлению может быть записана как: 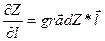 . Градиент показывает направление наибыстрейшего роста функции в данной точке.
. Градиент показывает направление наибыстрейшего роста функции в данной точке.
Экстремум функции двух переменных
Пусть Z=f(M) определена в некоторой окрестности точки M0(x0;y0).
Определение: Функция Z=f(x;y), имеет в точке М0 локальный максимум/минимум, если существует такая окрестность точки М0. в которой для каждой точки М из этой окрестности выполняется неравенство: f(M)£f(M0)- максимум / f(M)³f(M0)- минимум.
Из определения следует, что если Z имеет экстремум в точке М0, то полное приращение может быть записано: DZ=f(M)-f(M0), DZ£0- для максимума и DZ³0- для минимума.
Теорема необходимое условие для локального экстремума: Если Z=f(x;y), имеет экстремум в точке М0, и в этой точке существуют частные производные первого порядка, то они равны нулю.
Док-во: зафиксируем одну из переменных у=у0, тогда Z-функция одной переменной(зависит только от х) и она имеет производную в точке х0 и экстремум в точке х0, тогда по необходимому условию экстремума для функции одной переменной: j’(x0)=0 => fx’(x0;y0)=0.
Теорема достаточное условие локального экстремума: Пусть в точке М0 возможного экстремума и некоторой её окрестности функция Z=f(x;y) имеет частные производные второго порядка. Обозначим: 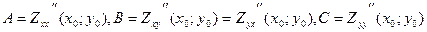 Составим матрицу:
Составим матрицу: 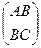 , обозначим D=
, обозначим D= 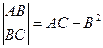 , тогда:
, тогда:
Если D>0, то точка М0 – является точкой локального экстремума,
Если D<0. то в точке М0 – экстремума нет,
Если D>0, A>0, М0 – точка минимума,
Если D>0, A<0, М0 – точка максимума.
Условный экстремум
условным экстремумом функции Z=f(x;y) называется экстремум этой функции при условии, что х и у связаны уравнением j(х;у)=0 – уравнением связи.
Если одна переменная может быть однозначно выражена через другую, то y=g(x) подставляем в функцию Z, и обычным способом находим экстремум функции одной переменной. Если это не возможно, то в общем случае задача на отыскание условного экстремума состоит в исследовании на обычный экстремум вспомогательной функции u, где u(x;y)=f(x;y)-lj(x;y), где l - неизвестный параметр =const.
Теорема необходимое условие условного экстремума: Чтобы точка М0 была точкой условного экстремума необходимо чтобы в ней выполнялось: 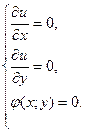 , где функция u – функция Лагранжа, l - множитель Лагранжа.
, где функция u – функция Лагранжа, l - множитель Лагранжа.
|
из
5.00
|
Обсуждение в статье: Производная по направлению и градиент |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

