 |
Главная |
Б) площадь плоской области, заданной параметрически
|
из
5.00
|
Пусть область  задана параметрически:
задана параметрически:





Примечание: если область  задана параметрически
задана параметрически  ;
;  . Тогда
. Тогда 
Применение определенного интеграла к вычислению площадей плоских областей заданных в полярной системе координат (19).

Пусть область  задана уравнением
задана уравнением  ,
,  , т.е. найдем площадь криволинейного сектора. Для этого разобьем область
, т.е. найдем площадь криволинейного сектора. Для этого разобьем область  лучами
лучами  на
на  частей с шагом
частей с шагом 

Т.к.  мало, то
мало, то  Следовательно этот элемент
Следовательно этот элемент  - равнобедренный треугольник с точностью до бесконечно малого. Его площадь
- равнобедренный треугольник с точностью до бесконечно малого. Его площадь  (по первому замечательному пределу). Итак
(по первому замечательному пределу). Итак  или в дифференциальной форме
или в дифференциальной форме  . Следовательно
. Следовательно 

Примечание: если область  задана уравнениями
задана уравнениями
 тогда площадь области
тогда площадь области  равна
равна


Применение определенного интеграла к вычислению объемов тел вращения (20).
а)Пусть область  задана уравнениями:
задана уравнениями:
 Область
Область  вращается вокруг
вращается вокруг  . Найдем
. Найдем  этого тела вращения.
этого тела вращения.
Разобьем тело вращения плоскостями перпендикулярными плоскости  . Обозначим:
. Обозначим: 
 -объем элементарного тела, на которое разделилось тело вращения. Т.к.
-объем элементарного тела, на которое разделилось тело вращения. Т.к.  мало, то
мало, то 
Следовательно 
Б) Пусть кривая x=g(y) непрерывна на отрезке [c,d] вращается вокруг оси Оу тогда:
Vy = 
 dy=g(y)
dy=g(y)  Vyi=
Vyi= 


В) Кривая y=f(x) определённая и непрерывная на [a,b] вращается вокруг оси OY

Разобьем это тело на элементарные области.  Объём тела
Объём тела 


Г) Кривая x=g(y) определённая и непрерывная на [c,d] вращается вокруг оси Ox
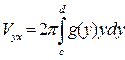
Применение определенного интеграла к вычислению площадей тел вращения (21)
Пусть кривая y=f(x) определена и дифференцируема на [a,b] вращается вокруг оси Ox, найдём площадь S поверхности этого тела вращения.

Отрезок [a,b] разбиваем точками x0=a, x1, x2…xn=b




где 
Аналогично  когда x=g(y) вращается вокруг оси Oy
когда x=g(y) вращается вокруг оси Oy
Физические приложения определенного интеграла работа, координаты центра масс плоской фигуры (22).
а) Работа силы F(x) по перемещению материальной точки вдоль оси Ox

б) Масса кривой y=f(x) на [a,b] если  - линейная плотность кривой, то
- линейная плотность кривой, то 
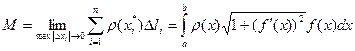
в) Статические моменты кривой относительно координатных осей.




г) Координаты центра тяжести кривой


Длина дуги плоской кривой (23).
а) кривая задана в декартовой системе координатуравнением  и
и  непрерывны на
непрерывны на  . Разбиваем отрезок
. Разбиваем отрезок  т.
т. 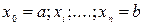 на n частей. Обозначим
на n частей. Обозначим 

 По теореме Пифагора
По теореме Пифагора 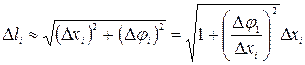 , но
, но  или в дифференциальной форме
или в дифференциальной форме
 . Тогда
. Тогда 
Б) длина дуги плоской кривой, заданной параметрически
Пусть кривая  задана уравнениями:
задана уравнениями:
 Тогда
Тогда 
При этом считаем, что функции  и
и  непрерывны на
непрерывны на  и
и 

Примечание:если кривая  - пространственная кривая, заданная уравнениями:
- пространственная кривая, заданная уравнениями: 
Длина дуги кривой в этом случае вычисляется по формуле 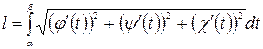
|
из
5.00
|
Обсуждение в статье: Б) площадь плоской области, заданной параметрически |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

