Линейное дифференциальное уравнение первого порядка. Уравнение Бернулли (32)

Д.у. вида 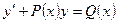, где 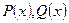-постоянные или непрерывные функции ~x называются линейными д.у. первого порядка. Неоднородным, если 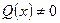и однородным, если 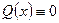. Его решение ищут в виде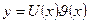

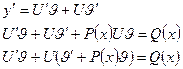
Так как у нас имеется лишняя степень свободы, то на одну из функции наложим дополнительное условие, в нашем случае потребуем, чтобы 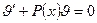, тогда для функции 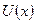получим уравнение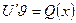

Итак,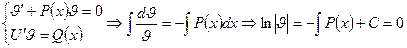

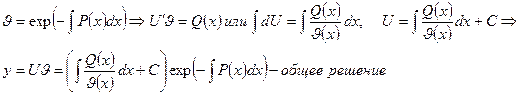
Замечание:линейное д.у. первого порядка, когда 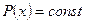, т.е. д.у. вида 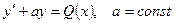может быть решено и другим способом, как линейное д.у. первого порядка с постоянными коэффициентами.

К линейным д.у. первого порядка примыкает и уравнение Бернулли, т.е. уравнение вида: 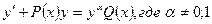Это уравнение можно привести к линейному д.у. подстановкой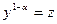

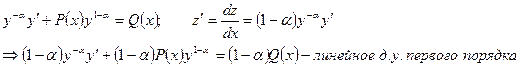
Замечание:

1) К уравнению Бернулли приводит задача о движении тела в среде, когда сила сопротивления среды зависит от скорости нелинейно, т.е.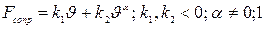

2) Решая уравнение Бернулли ищут , не приводя его к линейному подстановкой 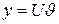, т.е. как линейное.

Уравнения в полных дифференциалах. Интегрирующий множитель (33).

Д.у. первого порядка вида 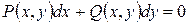называется дифференциальным уравнением в полных дифференциалах, если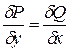

Это отношение является необходимым и достаточным условием, чтобы д.у. 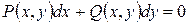было д.у. в полных дифференциалах, т.е. 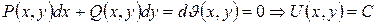- общий интеграл.

Действительно:

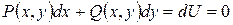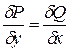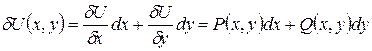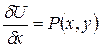1) Необходимость: докажем, что если , то , так как , то и 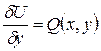Отсюда находим 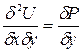и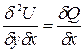

Но 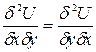, если они непрерывны в данной точке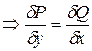

2) Достаточность: Пусть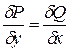

Докажем, что существует 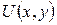такая, что 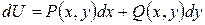Отсюда следует 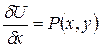и 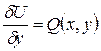. Проинтегрируем любое из этих уравнении по x или по y соответственно, например первое.

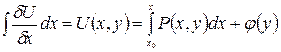
Итак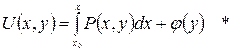

Отсюда находим

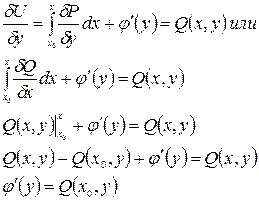
Отсюда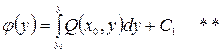

Из (*) и (**) следует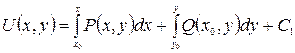

Общий интеграл исходного д.у. есть 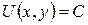и следовательно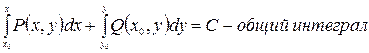

Замечание:из доказательства пункта 2 следует метод решения уравнений в полных дифференциалах, т.е. из условий 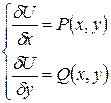ищется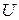

Если д.у. 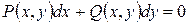не является д.у. в полных дифференциалах, т.е. 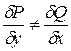, то существует такой множитель 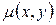, который называется интегрируемым множителем, что д.у. 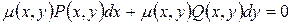будет д.у в полных дифференциалах, т.е. 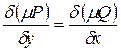(3) Это уравнение является д.у. частных производных для нахождения функции 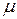. В двух частных случаях уравнение легко решится:

1) 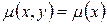Из уравнения (3) находим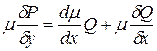

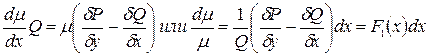(4)

Если это так, то 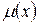находится из (4):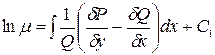

2) 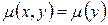Из уравнения (3) находим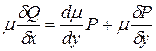

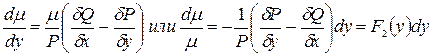(5)

Если это так, то 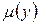находится из (5):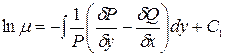

Замечание:д.у. в полных дифференциалах может быть как д.у. с разделяющимися переменными, однородным или линейным. Следовательно, перед тем как проверять условие 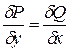необходимо убедиться, что оно не является д.у. с разделяющимися переменными, однородным, линейным или уравнением Бернулли. (смотрите последний пример)

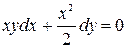д.у. с разд. переменными и однородным.

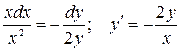- однородное.