 |
Главная |
Закон Био-Савара-Лапласа
|
из
5.00
|
ЛАБОРАТОРНАЯ РАБОТА № 2.6
«Определение горизонтальной и вертикальной
Составляющей напряженности магнитного поля Земли»
Цель работы: определить экспериментально горизонтальную составляющую земного магнитного поля на данной широте с помощью тангенс-буссоли и горизонтальную и вертикальную составляющую магнитного поля с помощью индуктора.
Теоретическая часть.
Магнитное поле – силовое поле, действующее на движущиеся заряды и на тела, обладающие магнитным моментом (магнитная стрелка, виток с током, диполь).
Источником магнитного поля являются намагниченные тела, проводники с током, движущиеся электрически заряженные тела.
Природа таких источников едина: магнитное поле возникает в результате движения микрочастиц (электронов, протонов, ионов и др.), а также благодаря наличию собственных магнитных моментов у микрочастиц.
Магнитное поле характеризуется вектором магнитной индукции  . Значение вектора магнитной индукции определяет силу, действующую на движущийся заряд или тело, имеющее магнитный момент.
. Значение вектора магнитной индукции определяет силу, действующую на движущийся заряд или тело, имеющее магнитный момент.
Вектор магнитной индукции характеризует результирующее магнитное поле, создаваемое всеми микро- и макротоками.
Микротоки – токи, обусловленные движением электронов в атомах и молекулах. Эти микроскопические токи и создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков.
Магнитное поле, созданное макротоками, описывается вектором напряженности 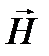 . В случае однородной среды вектор магнитной индукции связан с вектором напряженности соотношением
. В случае однородной среды вектор магнитной индукции связан с вектором напряженности соотношением

где  Гн/м - магнитная постоянная;
Гн/м - магнитная постоянная; 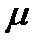 - магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков усиливается за счет поля микротоков среды.
- магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков усиливается за счет поля микротоков среды.
Закон Био-Савара-Лапласа
Этот закон позволяет рассчитать (определить) магнитное поле в произвольной точке, положение которой задается радиус-вектором  , проведенным от элемента тока dlк точке, в которой вычисляется магнитное поле.
, проведенным от элемента тока dlк точке, в которой вычисляется магнитное поле.
Тогда магнитная индукция поля, создаваемого произвольным элементом тока, определяется формулой

Модуль вектора магнитной индукции определяется выражением:

Вектор индукции магнитного поля перпендикулярен плоскости в которой лежали вектора  и
и  , а его направление определяется по правилу правого винта (рис. 1).
, а его направление определяется по правилу правого винта (рис. 1).

Рис. 1
Рассмотрим магнитное поле в центре кругового проводника с током.
Все элементы кругового проводника с током создают в центре магнитное поле одинакового направления – вдоль нормали от витка (рис. 2).

Рис. 2
Направление 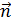 ,
, 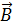 и
и  определяется правилом буравчика: за направление
определяется правилом буравчика: за направление 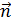 ,
, 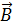 и
и  принимается направление поступательного движения буравчика, ручка которого вращается в направлении тока, текущего в контуре.
принимается направление поступательного движения буравчика, ручка которого вращается в направлении тока, текущего в контуре.
Поэтому сложение векторов (рис. 2)  можно заменить сложением их модулей. Так как все элементы перпендикулярны радиусу и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, используя закон Био-Савара-Лапласа
можно заменить сложением их модулей. Так как все элементы перпендикулярны радиусу и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, используя закон Био-Савара-Лапласа  , запишем
, запишем
 .
.
Так как sinα=1(dl^r), то

Учитывая, что H=B/μμ0, имеем:

|
из
5.00
|
Обсуждение в статье: Закон Био-Савара-Лапласа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

