Критерий согласия Колмогорова. Пусть по некоторой выборке х1, , хn, извлеченной из генеральной совокупности

Пусть по некоторой выборке х₁, …, х_n, извлеченной из генеральной совокупности, построена функция распределения F_Э(х). Нулевая гипотеза Н₀ будет состоять в том, что функция распределения генеральной совокупности F(x) совпадает с некоторой непрерывной функцией F₀(x). Альтернативной будет гипотеза Н₁: F(x) ¹ F₀(x).

В качестве статистики используем СВ

D_n = .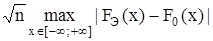

В случае справедливости гипотезы Н₀выполняется соотношение

Р(D_n < z) » K(z),

где K(z) – функция распределения Колмогорова (см. приложение VII).

По заданному уровню значимости a найдем z_{1 - a} (квантиль порядка
1 –a функции распределения K(z)).

Согласно критерию согласия Колмогорова: если D_n < z_{1 - a}, то гипотеза Н₀ принимается, т.е. F(x) = F₀(x), если D_n ³ z_{1 - a}, то верна гипотеза Н₁, т.е.
F(x) ¹ F₀(x).

П р и м е р 1. Результаты измерений 1000 деталей представлены в таблице 1.

Таблица 1.

xk		88,5		89,5		90,5		91,5		92,5
mk											S=1000

Проверить на уровне значимости a = 0,05, пользуясь критерием согласия Колмогорова, гипотезу Н₀: СВ Х распределена по нормальному закону с параметрами 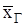= 90,25; s² = 1.

Решение. Критерий Колмогорова удобно применять по схеме.

1. Строятся эмпирическая и теоретическая функции распределения F_Э(х) и F₀(x).

2. Определяется величина

D_n = .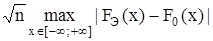

3. Если D_n < z_{1 - a}, то гипотеза Н₀ принимается, если D_n ³ z_{1 - a}, то гипотеза Н₀ отвергается.

Результаты вычислений будем заносить в таблицу 2.

Таблица 2.

i	xi	xi –			FЭ(xi)	|F0(x) – FЭ(x)|
	88,0	– 2,25	– 0,4877	0,0123	0,0105	0,0018
	88,5	– 1,25	– 0,4599	0,0401	0,0445	0,0044
	89,0	– 1,25	– 0,3944	0,1056	0,1115	0,0059
	89,5	– 0,75	– 0,2734	0,2266	0,2340	0,0074
	90,0	–0,25	– 0,0987	0,4013	0,4035	0,0022
	90,5	0,25	0,0987	0,5987	0,5945	0,0042
	91,0	0,75	0,2734	0,7734	0,7660	0,0074
	91,5	1,25	0,3944	0,8944	0,8855	0,0089
	92,0	1,75	0,4599	0,9599	0,9545	0,0054
	92,5	2,25	0,4877	0,9877	0,9875	0,0002

Значения для F_Э(x_i) вычислялись по формуле

.

Найдем значение D_n

D_n = .

Из таблицы VII получим z_{1 – 0,05} = z_0,95 = 1,36. Поскольку D_n < z_{1 – 0,05}, то гипотеза Н₀ принимается.

Критерий Колмогорова получил широкое распространение благодаря своей простоте. Однако принципиально его применение возможно, если известны все параметры распределения генеральной совокупности, чего практически не бывает. Если в качестве неизвестных параметров взять соответствующие им выборочные оценки, то для небольших выборок получается завышенное значение K(z), что может привести к принятию неверной гипотезы Н₀.

Следующий критерий согласия учитывает это обстоятельство, поэтому применим в тех случаях, когда параметры распределения неизвестны.

2.2. Критерий согласия Пирсона (c²).

Пусть Н₀ состоит в том, что F(x) = F₀(x); альтернативная гипотеза Н₁: F(x) ¹ F₀(x). В критерии согласия Пирсона статистикой берется случайная величина c², эмпирическое значение которой определяется по формуле

,

где k – число интервалов, на которые разбивается значение изучаемой СВ Х; m_i – частота i интервала; p_i – вероятность попадания СВ Х в i-тый интервал, вычисленная для теоретического закона распределения.

При n ® ¥ СВ стремится к распределению c² с l = k – r – 1 степенями свободы, где k – число интервалов, r – число параметров теоретического распределения, вычисленных по экспериментальным данным.

Требование, чтобы n ® ¥, является существенным. На практике достаточным считается объем n ³ 50 и число наблюдений в каждом интервале m_i не менее 5. Если в каком-нибудь интервале m_i < 5, то имеет смысл объединить соседние интервалы.

Изложим алгоритм применения критерия c².

1. Находится величина

.

2. Для выбранного уровня a по приложению VI находят значение , где l = k – r – 1.

3. Если £ , то гипотеза Н₀ принимается, т.е. можно считать, что теоретический и эмпирический законы распределений совпадают; если
> , то гипотеза Н₀ отвергается.

П р и м е р 2. При посеве семян льна важным показателем является глубина заделки семян. Для оценки посева было произведено 100 измерений. Результаты измерений приведены в таблице 3.

Таблица 3.

Глубина (см)	0,5-0,8	0,8-1,1	1,1-1,4	1,4-1,7	1,7-2,0	2,0-2,3	2,3-2,6	2,6-2,9
Число наблюдений

С помощью критерия c² проверить гипотезу Н₀ о нормальном распределении СВ Х – глубины заделки семян на уровне значимости a = 0,01.

Решение. Найдем и S_В по выборочным данным

.

.

Поскольку в крайних интервалах значение m_i < 5, объединим их.

Таблица 4.

Глубина (см)	менее 1,4	1,4-1,7	1,7-2,0	2,0-2,3	более 2,3
Число наблюдений

1. Найдем вероятности p_i попадания СВ Х в i интервал по формуле

,

где значения 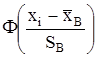найдем, используя таблицу II приложений.

;

;

;

;

.

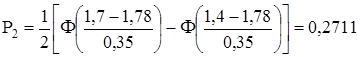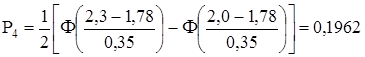Проверка: .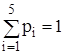

Вычислим значение :

2. l = k – r – 1 = 5 – 2 – 1 = 2. По таблице II найдем 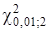= 9,21.

3. Поскольку < 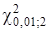, то гипотезу Н₀ о нормальном распределении СВ Х отвергать нет оснований.

 

Примеры для самостоятельного решения.

По условиям примеров для лабораторной работы №2 (для своего варианта) проверить на уровне значимости 0,05 гипотезу Н₀: соответствующая выборка извлечена из нормально распределенной совокупности, используя:

а) критерий согласия c²;

б) критерий согласия Колмогорова.

 

Приложение VI.

Значения критерия c² (хи-квадрат)

Число степеней свободы	Вероятность a
0,99	0,98	0,95	0,90	0,80	0,70	0,50	0,30	0,20	0,10	0,05	0,02	0,01
	0,00	0,00	0,00	0,02	0,06	0,15	0,45	1,07	1,64	2,71	3,84	5,41	6,64
	0,02	0,04	0,10	0,21	0,45	0,71	1,39	2,41	3,22	4,60	5,99	7,82	9,21
	0,11	0,18	0,35	0,58	1,00	1,42	2,37	3,66	4,64	6,25	7,82	9,84	11,3
	0,30	0,43	0,71	1,06	1,65	2,20	3,36	4,88	5,99	7,78	9,49	11,7	13,3
	0,55	0,75	1,14	1,61	2,34	3,00	4,35	6,06	7,29	9,24	11,1	13,4	15,1
	0,87	1,13	1,63	2,20	3,07	3,83	5,35	7,23	8,56	10,6	12,6	15,0	16,8
	1,24	1,56	2,17	2,83	3,82	4,67	6,35	8,38	9,80	12,0	14,1	16,6	18,5
	1,65	2,03	2,73	3,49	4,59	5,53	7,34	9,52	11,0	13,4	15,5	18,2	20,1
	2,09	2,53	3,32	4,17	5,38	6,39	8,34	10,7	12,2	14,7	16,9	19,7	21,7
	2,56	3,06	3,94	4,86	6,18	7,27	9,34	11,8	13,4	16,0	18,3	21,2	23,2
	3,05	3,61	4,58	5,58	6,99	8,15	10,3	12,9	14,6	17,3	19,7	22,6	24,7
	3,57	4,18	5,23	6,30	7,81	9,03	11,3	14,0	15,8	18,5	21,0	24,1	26,2
	4,11	4,76	5,89	7,04	8,63	9,93	12,3	15,1	17,0	19,8	22,4	25,5	27,7
	4,66	5,37	6,57	7,79	9,47	10,8	13,3	16,2	18,1	21,1	23,7	26,9	29,1
	5,23	5,98	7,26	8,55	10,3	11,7	14,3	17,3	19,3	22,3	25,0	28,3	30,6
	5,81	6,61	7,96	9,31	11,1	12,6	15,3	18,4	20,5	23,5	26,3	29,6	32,0
	6,41	7,26	8,67	10,1	12,0	13,5	16,3	19,5	21,6	24,8	27,6	31,0	33,4
	7,02	7,91	9,39	10,9	12,9	14,4	17,3	20,6	22,8	26,0	28,9	32,3	34,8
	7,63	8,57	10,1	11,6	13,7	15,3	18,3	21,7	23,9	27,2	30,1	33,7	36,2
	8,26	9,24	10,8	12,4	14,6	16,3	19,3	22,8	25,0	28,4	31,4	35,0	37,6
	8,90	9,92	11,6	13,2	15,4	17,2	20,3	23,9	26,2	29,6	32,7	36,3	38,9
	9,54	10,6	12,3	14,0	16,3	18,1	21,3	24,9	27,3	30,8	33,9	37,7	40,3
	10,2	11,3	13,1	14,8	17,2	19,0	22,3	26,0	28,4	32,0	35,2	39,0	41,6
	10,9	12,0	13,8	15,7	18,1	19,9	23,3	27,1	29,6	33,2	36,4	40,3	43,0
	11,5	12,7	14,6	16,5	18,9	20,9	24,3	28,2	30,7	34,4	37,7	41,7	44,3
	12,2	13,4	15,4	17,3	19,8	21,8	25,3	29,2	31,8	35,6	38,9	42,9	45,6
	12,9	14,1	16,1	18,1	20,7	22,7	26,3	30,3	32,9	36,7	40,1	44,1	47,0
	13,6	14,8	16,9	18,9	21,6	23,9	27,3	31,4	34,0	37,9	41,3	45,4	48,3
	14,3	15,6	17,7	19,8	22,5	24,6	28,3	32,5	35,1	39,1	42,6	46,7	49,6
	14,9	16,3	18,5	20,6	23,4	25,5	29,3	33,5	36,2	40,3	43,8	48,0	50,9

 

Приложение VII.

Приближенные значения функции Колмогорова, домноженные на 10⁵

zкр	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5						105	105	105	105	105

 

 

* Предложенная статистика является СВ, поскольку в различных опытах значения и могут принимать различные заранее неизвестные значения.