 |
Главная |
Доказательство окончено
|
из
5.00
|
РАЗЛОЖЕНИЕ БУЛЕВСКИХ ФУНКЦИЙ
ПО ПЕРЕМЕННЫМ
Рассмотрим вопрос о нахождении способа представления произвольных функции из P2с помощью формул над множеством элементарных функций.
Решение этого вопроса практически важно, поскольку делает возможным не только прямой переход от формульных представлений булевских функций к их табличному заданию, но и обратный: от табличного задания функций к их формульному представлению. Кроме того, формульное представление функций из P2 может оказаться более компактным по сравнению с табличным заданием.
Введем в рассмотрение специальную функцию двух переменных

Данная функция имеет следующее табличное задание:
| x s | xs |
| 0 0 | |
| 0 1 | |
| 1 0 | |
| 1 1 |
Из этого следует, что xs = 1 тогда и только тогда, когда x = s.
ОПРЕДЕЛЕНИЕ
Конъюнкцией ранга r называется всякая формула K, имеющая вид:  .
.
Булевскую функцию, представляемую конъюнкцией некоторого ранга, будем также называть конъюнкцией этого ранга, или просто конъюнкцией.
Очевидно, что K =  принимает значение 1на единственном наборе значений своих переменных, для которого выполнены условия:
принимает значение 1на единственном наборе значений своих переменных, для которого выполнены условия:  . Поэтому для всякого конкретного набора значений переменных x1, . . . , xn однозначно определяется конъюнкция ранга n, принимающая значение 1 только на этом наборе. Например, для набора
. Поэтому для всякого конкретного набора значений переменных x1, . . . , xn однозначно определяется конъюнкция ранга n, принимающая значение 1 только на этом наборе. Например, для набора
(0,0,1,0,1) значений переменных x1, . . ., x5 соответствующая конъюнкция имеет вид
 . (1)
. (1)
Тогда, если булевская функция f(x1, . . . , xn) принимает значение 1 лишь на двух наборах значений переменных
(s1, . . . , sn) и (d1, . . . , dn), то справедливо равенство:
f (x1, . . . , xn) =
 Ú
Ú  . (2)
. (2)
Подобным образом можно выписать формулу, представляющую произвольную булевскую функции f, если заданы все наборы, на которых она равна 1.
Приведенные два примера (1) и (2) представлений булевских функций формулами являются частными случаями следующей общей теоремы.
ТЕОРЕМА 4.2
(О разложении булевских функций по переменным)
Пусть f (x1 , . . . , xn ) Î P2 и 1 £ m £ n.
Тогда справедливо следующее тождество:
f(x1 , . . . , xn ) =
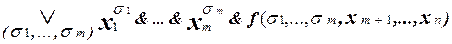 . (1)
. (1)
Замечание. Здесь запись  означает дизъюнкцию конъюнкций ранга n, составленных для всех возможных двоичных наборов (s1, . . . , sn) значений переменных x1, . . . , xn.
означает дизъюнкцию конъюнкций ранга n, составленных для всех возможных двоичных наборов (s1, . . . , sn) значений переменных x1, . . . , xn.
Доказательство
Покажем, что для каждого набора (s1, . . . , sn) значений переменных функции f значения, принимаемые функциями в левой и правой частях равенства (1), совпадают.
Значение, принимаемое функцией слева, равно f  .
.
Рассмотрим правую часть равенства (1). Подставив в него выбранные значения переменных, получим запись:
 .
.
Учитывая, что  = 1 тогда и только тогда, когда " i=1, . . . ,m (gi = si), из полученного выражения можно удалить все элементы дизъюнкции, которые принимают значение равное нулю, и получить выражение:
= 1 тогда и только тогда, когда " i=1, . . . ,m (gi = si), из полученного выражения можно удалить все элементы дизъюнкции, которые принимают значение равное нулю, и получить выражение:  .
.
Так как  = 1, то последнее выражение равно:
= 1, то последнее выражение равно:  . То есть значения, принимаемые левой и правой частями равенства (1) на наборе значений переменных (s1, . . . , sn), равны.
. То есть значения, принимаемые левой и правой частями равенства (1) на наборе значений переменных (s1, . . . , sn), равны.
Доказательство окончено.
Рассмотрим несколько специальных случаев доказанной теоремы.
1. Разложение по одной переменной (m = 1)
f(x1 , . . . , xn ) = 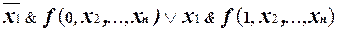 .
.
2. Разложение по всем переменным (m = n).
f(x1, . . ., xn ) = 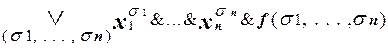
В случае, когда булевская функция f(x1 , . . . , xn ) отлична от тождественного нуля, разложение по всем переменным можно записать в виде:
f(x1, . . . , xn) =  .
.
Такое представление булевой функции называется совершенной дизъюнктивной нормальной формой этой функции или СДНФ для f.
СЛЕДСТВИЕ. Всякая булевская функция представима формулой над множествомB = {&, Ú, ` }.
Действительно, если f отлична от тождественного нуля, то она может быть представлена в виде СДНФ этой функции, в которую входят конъюнкции, дизъюнкции и отрицания. Если же f является тождественно равной нулю функцией, то f можно представить в виде  .
.
|
из
5.00
|
Обсуждение в статье: Доказательство окончено |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

