 |
Главная |
Исследование функции и построение её графика
|
из
5.00
|
Функция  называется монотонно возрастающей в интервале хÎ(а,b), если для любых двух точек х1 и х2 этого интервала из неравенства х2>х1 следует неравенство
называется монотонно возрастающей в интервале хÎ(а,b), если для любых двух точек х1 и х2 этого интервала из неравенства х2>х1 следует неравенство  >
> 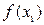 , то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.
, то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.
Функция  называется монотонно убывающейна интервале хÎ(а,b), если для любых двух точек х1 и х2 этого интервала из неравенства х2>х1 следует неравенство
называется монотонно убывающейна интервале хÎ(а,b), если для любых двух точек х1 и х2 этого интервала из неравенства х2>х1 следует неравенство  <
< 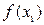 , то есть если любому большему значению аргумента из этого интервала соответствует меньшее значение функции.
, то есть если любому большему значению аргумента из этого интервала соответствует меньшее значение функции.
Интервалы возрастания и убывания функции называются интервалами монотонности функции.
Достаточный признак монотонности дифференцируемой функции:если на интервале хÎ(а, b) производная  сохраняет знак, то функция
сохраняет знак, то функция  сохраняет монотонность на этом интервале, а именно:
сохраняет монотонность на этом интервале, а именно:
если  , то
, то  монотонно возрастает;
монотонно возрастает;
если  , то
, то  монотонно убывает.
монотонно убывает.
Точка х0 называется точкой максимума функции  , если существует такая двухсторонняя окрестность точки х0 , что для всякой точки х¹х0 этой окрестности выполняется неравенство
, если существует такая двухсторонняя окрестность точки х0 , что для всякой точки х¹х0 этой окрестности выполняется неравенство 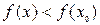 . При этом число
. При этом число  называется максимумомфункции
называется максимумомфункции  .
.
Аналогично, если для всякой точки х¹х0 из некоторой окрестности точки х0 выполняется неравенство  , то х0 называется точкой минимума, а число
, то х0 называется точкой минимума, а число  – минимумомфункции
– минимумомфункции  .
.
Экстремумамифункции называются ее максимумы и минимумы. Точками экстремума функции называются её точки максимума и минимума.
Понятие экстремума связано с наличием окрестности точки х0 из области определения функции. Поэтому функция может иметь экстремум лишь во внутренних точках области определения.
Необходимое условие экстремума:если непрерывная функция  имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует. Точки, в которых производная равна нулю или не существует, называются критическими точками функции
имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует. Точки, в которых производная равна нулю или не существует, называются критическими точками функции  .
.
Необходимое условие экстремума не является достаточным, т.е. точки, в которых  или же
или же  не существует, необязательно являются точками экстремумов функции.
не существует, необязательно являются точками экстремумов функции.
Достаточные условия экстремума:если при переходе через критическую точку х0 (слева направо) производная  изменяет свой знак, то в точке х0 есть экстремум причем, это максимум, если знак
изменяет свой знак, то в точке х0 есть экстремум причем, это максимум, если знак  меняется с плюса на минус, и это минимум, если знак
меняется с плюса на минус, и это минимум, если знак  меняется с минуса на плюс. Если при переходе через критическую точку х0 производная
меняется с минуса на плюс. Если при переходе через критическую точку х0 производная  не изменяет свой знак, то в точке х0 нет экстремума функции
не изменяет свой знак, то в точке х0 нет экстремума функции  .
.
----------------------------------------------------------------------------------------------------------------
Исследование функции и построение её графика. Стр.1
График функции  называется выпуклым(или выпуклым вверх) на интервале xÎ(a;b), если он расположен ниже любой касательной, проведенной к графику на этом интервале.
называется выпуклым(или выпуклым вверх) на интервале xÎ(a;b), если он расположен ниже любой касательной, проведенной к графику на этом интервале.
График функции  называется вогнутым (или выпуклым вниз) на интервале xÎ(a;b), если он расположен выше любой касательной, проведенной к графику на этом интервале.
называется вогнутым (или выпуклым вниз) на интервале xÎ(a;b), если он расположен выше любой касательной, проведенной к графику на этом интервале.
Точка графика непрерывной функции  , отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
В простейших случаях область определения функции можно разбить на конечное число интервалов с постоянным направлением выпуклости.
 Например, при xÎ(a;х0) график выпуклый, при xÎ(х0;b) вогнутый, М0(х0;y0) – точка перегиба.
Например, при xÎ(a;х0) график выпуклый, при xÎ(х0;b) вогнутый, М0(х0;y0) – точка перегиба.

В точке перегиба касательная пересекает график (конечно, при условии, что касательная существует в этой точке).
Достаточное условие выпуклости, вогнутости:если функция  является дважды дифференцируемой и ее
является дважды дифференцируемой и ее 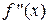 сохраняет знак при всех xÎ(a;b), то график функции имеет постоянное направление выпуклости на этом интервале:
сохраняет знак при всех xÎ(a;b), то график функции имеет постоянное направление выпуклости на этом интервале:
при 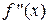 <0 – выпуклость вверх,
<0 – выпуклость вверх,
при 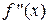 >0 – вогнутость (выпуклость вниз).
>0 – вогнутость (выпуклость вниз).
Необходимое условие для точки перегиба: если x0 – абсцисса точки перегиба графика функции  , то
, то  или
или  не существует.
не существует.
Необходимое условие для точки перегиба не является достаточным. Точки, принадлежащие графику функции  , в которых
, в которых  или
или 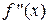 не существует, называются подозрительными на перегиб или критическими точками функции
не существует, называются подозрительными на перегиб или критическими точками функции  по её второй производной.
по её второй производной.
Достаточное условие для точек перегиба:если вторая производная 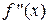 при переходе через точку х0, подозрительную на перегиб, изменяет знак, то точка графика с абсциссой х0 является точкой перегиба. Если
при переходе через точку х0, подозрительную на перегиб, изменяет знак, то точка графика с абсциссой х0 является точкой перегиба. Если 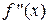 не изменяет знак при переходе через точку х0, то перегиба нет.
не изменяет знак при переходе через точку х0, то перегиба нет.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.
Для кривой, которая является графиком функции  , различают вертикальные, наклонные и горизонтальные асимптоты.
, различают вертикальные, наклонные и горизонтальные асимптоты.
----------------------------------------------------------------------------------------------------------------
Исследование функции и построение её графика. Стр.2

Прямая х=а является вертикальной асимптотой графика функции  , если выполняется хотя бы одно из условий:
, если выполняется хотя бы одно из условий:  или
или 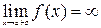 , т.е. если значение х=а является точкой разрыва второго рода функции или границей ее области определения.
, т.е. если значение х=а является точкой разрыва второго рода функции или границей ее области определения.
Прямая  является наклонной (при k=0 горизонтальной) асимптотой графика функции
является наклонной (при k=0 горизонтальной) асимптотой графика функции  , если существуют конечные пределы
, если существуют конечные пределы
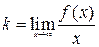 и
и  . (1)
. (1)
Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая  наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
При практическом вычислении пределы (1) могут быть различными при х®+¥ и при х®–¥.
Полное исследование функций и построение их графиков удобно выполнять по следующей схеме:
1) найти область определения функции, точки разрыва;
2) выяснить, не является ли функция чётной или нечётной, периодической;
3) найти точки пересечения с осями координат и промежутки знакопостоянства;
4) найти асимптоты графика функции;
5) исследовать монотонность функции и найти ее экстремумы;
6) найти точки перегиба, установить интервалы выпуклости и вогнутости графика функции;
7) используя результаты исследования, построить график функции.
|
из
5.00
|
Обсуждение в статье: Исследование функции и построение её графика |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

