 |
Главная |
Лекция 3. МЕТОДЫ ПРОГНОЗИРОВАНИЯ СОЦИАЛЬНО- ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ
|
из
5.00
|
Основные понятия: эксперт; качественные оценки; метод интервью; метод анкетирования; метод комиссии; количественные оценки; скользящая средняя; метод делъфи; случайная величина; выборка; генеральная совокупность; регрессионное уравнение; метод наименьших квадратов; временной ряд.
В современной экономической науке существует множество методов прогнозирования. Их объединяет возможность решать конкретные прогностические задачи. Для того чтобы понять существо и специфику различных методов прогнозирования (МП), рассмотрим их основное содержание и классификационные группы.
3.1.Понятие, виды и методы прогнозирования. Метод прогнозирования (МП) - определенная система правил, приемов и процедур, позволяющая получить прогноз. Классификация МП осуществляется по различным признакам. Важнейшим из них является степень формализации процесса обработки информации и получения прогноза, которая проявляется в особенностях применяемого методологического аппарата.
С этой точки зрения методы прогнозирования можно подразделить на две больших группы: экспертные (интуитивные) методы; методы, основанные на применении аппарата математической статистики. Среди последних выделяются: прогнозирование случайной величины по выборке значений; прогнозирование с использованием регрессионной зависимости; прогнозирование временных рядов.
В реальной действительности прогнозы строятся, как правило, на сочетании различных методик. Например, при экспертном прогнозировании (обычно при обработке исходной информации) применяются определенные методы математической статистики. И наоборот, каким бы мощным не был математический аппарат, использованный для получения того или иного прогноза, все равно значительную роль играет опыт и интуиция прогнозиста. Тем не менее, обычно один из методой является доминирующим при получении конкретного прогноза. Каждый из них имеет свои существенные особенности.
3.2. Экспертные (интуитивные) методы прогнозирования. Данный метод прогнозирования обычно применяется в следующих случаях:
отсутствии достаточного объема достоверной информации об объекте прогнозирования - т. е. нет информации об аналогичных объектах прогнозирования или о состоянии самого объекта прогнозирования в прошлом;
неопределенности состояния среды, в которой будет происходить функционирование объекта прогнозирования в прогнозируемом периоде (внешней среды);
большом временном горизонте прогнозирования, т. е. прогнозировании на большой срок, в этом случае фактически имеем комбинацию двух предыдущих случаев — нет достоверной информации по епмом объекте прогнозирования и о его внешней среде.
Реализация экспертного (интуитивного) метода предполагает следующую последовательность действий: 1) поиск экспертов; 2) отбор экспертов; 3) опрос экспертов; 4) обработку результатов. Коротко рассмотрим существо каждого из этих этапов.
Поиск экспертов направлен на выявление первоначального круга лиц, являющихся потенциальными кандидатами в эксперты. Это можно сделать по публикациям, так как авторы, пишущие об объекте прогнозирования, как правило, не только хорошо знакомы с самим объектом, но и зачастую являются наиболее компетентными людьми но данному вопросу. Вторым способом выявления кандидатов в эксперты является опрос о потенциальных кандидатах среди специалистов хотя бы отдаленно знакомых с объектом прогнозирования.
Наиболее простым методом отбора экспертов является выбор тех кандидатов, чьи фамилии наиболее часто назывались на этапе поиска кандидатов в эксперты. Вторым методом может служить процедура самооценки или, что значительно лучше, оценки каждым кандидатом всех остальных кандидатов. При оценке экспертами друг друга результаты оценки получаются значительно более объективными, чем при самооценке, но в этом случае кандидаты должны хорошо знать друг друга. Если это условие не выполняется, то применяется процедура самооценки. Последним методом отбора экспертов из списка кандидатов может служить метод контрольных вопросов. В этом случае кандидатам задаются вопросы об объекте прогнозирования, ответы на которые не известны кандидатам, но точно известны организаторам прогноза. Лучшими экспертами являются те кандидаты, которые дали наиболее точные ответы на контрольные вопросы.
Опрос экспертов, как правило, дает наиболее точные результаты в том случае, если они отвечают на заранее поставленные вопросы. Вопросы могут быть следующих видов: открытые - не имеют готовых вариантов ответа; закрытые - экспертам предлагается выбрать один из предложенных вариантов; косвенные — вопросы, применяемые в тех случаях, когда ответ эксперта может характеризовать его морально-психологические качества и существует опасность того, что эксперт не будет при ответе полностью искренним, т. е. может исказить ответ по этическим соображениям.
По методу проведения опросы могут быть индивидуальными или коллективными, очными или заочными. К достоинствам индивидуального метода опроса следует отнести его меньшую трудоемкость, так как нет необходимости в обеспечении одновременной явки всех экспертов на заседание. Коллективный опрос более трудоемок в части подготовки заседания, при коллективном обсуждении наблюдается эффект психологического давления мнения большинства и мнения наиболее авторитетных экспертов. Заочные опросы менее трудоемки, чем очные, но в них всегда существует опасность того, что эксперт неверно понимает вопрос, а у проводящего опрос нет возможности это выявить. Для очных опросов все характерно с точностью до наоборот: они более трудоемки, но меньше опасность получить ответы на неверно понятые вопросы.
Задача обработки полученных результатов предполагает поиск ответа на два вопроса: первый - чему собственно равен коллективный ответ экспертов, второй - можно ли им доверять. Способ ее решения зависит от характера ответов, которые могут быть количественными или качественными. В первом случае в качестве конечного результата может быть принято среднее значение ответов. Но эта величина часто не является лучшим выражением коллективного мнения экспертов, так как она может сильно меняться при наличии значительно отличающихся мнений, особенно в тех случаях, когда эти сильно отличающиеся мнения несимметричны, т. е. число оптимистов не равно числу пессимистов. Более правильно считать, что коллективное мнение экспертов точнее оценивается медианой. Медиана - это такое значение, которое делит все ответы экспертов пополам, одна половина ответов меньше медианы, вторая - больше.
Ответ на вопрос о том, можно ли доверять мнению экспертов, решается с помощью оценки степени согласованности их мнений. И оспине такого решения лежит подход, основанный на здравом смысле: мы склонны верить утверждению других, когда все высказывают не слишком различающиеся мнения. С целью оценки степени согласованности мнения экспертов необходимо найти первую и третью квартили. Кварта в переводе с латинского - четверть. Первая квартиль это такое значение, которое делит ответы экспертов в пропорции: один четвертая и три четвертых. Одна четвертая - это ответы меньше первой квартили, три четвертых - ответы, которые больше первой квартили. Третья квартиль делит ответы экспертов соответственно в пропорции: три четвертых и одна четвертая. Три четвертых это ответы, которые меньше третьей квартили, а одна четверть - ответы, которые больше. Считается, что мнение экспертов согласовано, если разность первой и третьей квартилей меньше медианы.
В тех случаях, когда прогнозируемый параметр не удается оценить в количественной шкале, его оценивают в качественной шкале. Полученные в этом случае качественные оценки представляют собой результаты ранжирования объектов, т. е. расположения их по степени возрастания или убывания оцениваемого параметра. Присвоенные объектам ранги говорят о степени выраженности измеряемого свойства, но не говорят, насколько это свойство сильнее или слабее выражено у объектов, имеющих разные ранги. Ранги могут присваиваться по возрастающей (чем сильнее выражено свойство, тем выше ранг) или по убывающей (чем сильнее свойство, тем меньше ранг). Процедура приведения ранговых оценок экспертов к сопоставимому виду называется стандартизацией рангов. Суть ее в том, что ранговые оценки различных экспертов приводятся к единой шкале, после чего определяются усредненные оценки вариантов и им присваиваются определенные итоговые ранги.
Кроме опроса (путем анкетирования, или проведения интервью) применяются и другие методы получения прогноза на основе мнения экспертов. К важнейшим из них относятся метод комиссии и метод дельфи.
При методе комиссии эксперты осуществляют прогнозирование, совместно обсуждая проблему. Это очный коллективный метод. Для прогнозирования по методу комиссии необходимо организовать встречу всех экспертов, для занятых людей это обычно далеко не просто осуществить. Но в результате возрастает точность прогнозирования так как нет проблемы неверно понятого вопроса (в процессе обсуждения легко выявляется неверное понимание сути обсуждаемого вопроса) и самое главное, у экспертов появляется возможность воспользоваться всем многообразием информации об объекте прогнозирования так как в процессе обсуждения эксперты высказывают различные точки зрения. В то же время в этом способе существует и ряд негативных моментов, в основном психологического характера, не позволяющих полностью реализовать все возможности по повышению точности прогнозирования.
Метод «дельфи» был разработан знаменитой консалтинговой фирмой «Рэнд корпарейшен» и назван в честь мифического дельфийского оракула-прорицателя, устами богов верно отвечавшего на любые вопросы жителей древней Греции. Он состоит из следующих этапов: 1) экспертам рассылаются вопросы; 2) для полученных ответов находятся медиана, первая и третья квартили; 3) всех экспертов из первой и последней четвертей просят привести доводы и обоснование своих прогнозов; 4) значение медианы, а также анонимные доводы экспертов, чьи прогнозы оказались в первой и последней четверти, рассылаются всем экспертам с просьбой еще раз осуществить прогнозирование с учетом этой дополнительной информации; 5) для полученных ответов вновь находятся медиана и первая, и третья квартили. Если мнение экспертов остается по-прежнему не согласованным, то шаги 3—5 повторяются до получения требуемой степени согласованности.
Важное значение имеет также метод сценариев. Он представляет собой комплексный метод прогнозирования сложных процессов со структурными сдвигами и заключается в установлении логически связанной последовательности событий поэтапного перехода из существующего состояния объекта прогнозирования в будущее состояние. При разработке сценариев используют прямой и обратный способы. При прямом способе последовательность смены событий выстраивается из прошлого в будущее, т. е. описываются наиболее вероятные последовательные изменения объекта прогнозирования из его нынешнего состояния в будущее. При обратном способе вначале описывается будущее (желаемое) состояние объекта прогнозирования, затем делается попытка сформулировать ближайшее предыдущее состояние, затем более отдаленное, вплоть до нынешнего состояния. Сочетание прямого и обратного подходов обычно позволяет получить наилучшие результаты.
Обычно прогнозирование по методу сценариев является многовариантным, наиболее часто составляются два или три варианта развития событий. При двухвариантном имеем дело с пессимистическим (наиболее неблагоприятным) вариантом развития событий и оптимистическим (наиболее благоприятным). Между этими вариантами находятся все остальные варианты развития событий. Ожидаемое значение прогнозируемых показателей определяются в этом случае как среднее арифметическое между оптимистической и пессимистической оценками.
3.3.Прогнозирование случайной величины по выборке значений. Задача прогнозирования по выборке возникает в том случае, когда имеются данные по нескольким объектам, аналогичным объектy прогнозирования по своим свойствам и на основании этой информации необходимо спрогнозировать состояние определенного объекта прогнозирования. Второй вариант — имеются данные о состоянии объекта прогнозирования в прошлом и необходимо на их основании спрогнозировать его состояние в будущем. В первом случае говорят, что имеются перекрестные данные, во втором - временные. Прогнозируемые величины часто изменяются не в соответствии с определенной функциональной зависимостью, а как случайные (или стохастические). Все возможные значения случайной величины - как прошлые, так и будущие, как известные так и неизвестные — называют генеральной совокупностью случайной величины. Любая часть этой генеральной совокупности называется выборкой. В прогнозировании генеральная совокупность всегда неизвестна, так как в противном случае нет самой задачи прогнозирования. В математической постановке задача прогнозирования по выборке выглядит следующим образом. Имеем выборку из генеральной совокупности мощностью N. По этой выборке необходимо оценить параметры генеральной совокупности и на их основании осуществить прогноз очередного значения случайной величины и определить меру точности полученного прогноза. Прогноз подобного рода осуществляется в три этапа: 1) предварительный анализ данных; 2) прогноз ожидаемого значения случайной величины; 3) оценка точности прогноза.
На этапе предварительного анализа данных обычно формируется гистограмма, которая представляет собой столбчатую диаграмму, по горизонтальной оси которой нанесены равномерные интервалы случайной величины, а по вертикальной - число попаданий случайной величины в эти интервалы.
Полученная гистограмма имеет более одной вершины (рис 3.1, а), это является сигналом того, что исходные данные представляют собой выборку не одной случайной величины, а являются суммой двух выборок двух разных случайных величин. Например, вместо перекрестных данных одного и того же класса имеются данные об объектах, принадлежащих двум разным классам, или данные о состоянии объекта прогнозирования в прошлом относятся к двум его разным состояниям — до каких-либо структурных изменений и после этих изменений. Поэтому исходные данные должны быть тщательно проанализированы на предмет удаления из них данных, не имеющих отношения к объекту прогнозирования. Заслуживают тщательного внимания и «выбросы» на гистограмме (рис 3.1,6), особенно если они расположены на некотором расстоянии от основной фигуры гистограммы. Данные, соответствующие выбросам, полезно детально изучить, так как они обычно сигнализируют о наличии сбоев в изучаемом процессе или иных отклонений от обычного хода дел. В случае если гистограмма напоминает симметричную одновершинную фигуру, то дальнейшая работа по прогнозированию может быть выполнена в предположении, что случайная величина имеет нормальное распределение, работа с которым наиболее проста ввиду хорошей теоретической изученности этого распределения и разнообразности разработанных для него приемов и методов обработки. В случае если это не так (рис 3.1, в), то необходимо воспользоваться каким-либо другим специальным распределением, что обычно усложняет задачу анализа.
Следует отметить, что визуальный анализ исходных данных по внешнему виду гистограммы является приближенным. Существуют более надежные статистические методы проверки обсуждавшихся ныне предположений, но они требуют больших выборок (обычно более 50–100 наблюдений), что редко встречается в практике прогнозирования и специальных методов обработки.
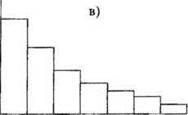 Рис. 3.1. Гистограмма случайных величин
Рис. 3.1. Гистограмма случайных величин
|
Следующий этап - определение ожидаемого значения случайной виличины. Для это используются следующие параметры: среднее значение и медиана (рассмотрены выше), мода, т. е. наиболее часто встречающееся значение (в переводе с латыни мода - это мера, правило). Рекомендации по выбору того, какая из трех рассмотренных выше характеристик генеральной совокупности случайной величины должна использоваться при прогнозировании, сводятся к следующему: 1) при прогнозировании одного единственного значения дискретной случайной величины наиболее оправдано использование моды; 2) при прогнозировании нескольких значений случайной величины предпочтительно использование медианы и только в том случае, когда есть уверенность, что случайная величина имеет симметричное распределение, может использоваться среднее значение, так как для симметричных распределений среднее значение и медиана совпадают.
Последний этап - оценка точности прогнозирования случайной величины. Наиболее простой способ охарактеризовать точность прогноза это указать размах колебаний значений случайной величины в выборке, который можно определить как разность между максимальным и минимальным значениями. Чем он больше, тем меньше точность прогноза. Но у этой характеристики есть существенный недостаток - при наличии выбросов (аномально больших и аномально малых значений) размах колебаний занижает оценку точности, так как реагирует только на них. Более строгими мерами точности прогноза являются дисперсия и стандартное отклонение.
Дисперсия - это средний квадрат отклонения случайной величины от своего среднего значения. Для генеральной совокупности дисперсия определяется по формуле
 (3.1)
(3.1)
где  i-e значение из генеральной совокупности случайной величины;
i-e значение из генеральной совокупности случайной величины;
 - ее среднее значение;
- ее среднее значение;
п — число значений случайной величины в генеральной совокупности.
Стандартное отклонение (второе название - среднеквадратическое отклонение) 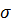 , равное корню квадратному от дисперсии, т. е.:
, равное корню квадратному от дисперсии, т. е.:
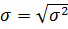 (3.2)
(3.2)
В отличие от дисперсии стандартное отклонение имеет ту же размерность, что и характеризуемая им случайная величина.
Для полной характеристики точности полученного прогноза необходимо еще построить и проанализировать функцию плотности распределения случайной величины и кумулятивную функцию ее распределения.
График кумулятивной функции распределения можно получить путем сглаживания гистограммы (рис. 3.2).
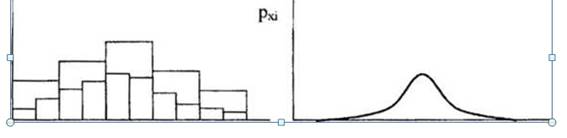 Рис. 3.2. Схема получения кривой плотности распределения
Рис. 3.2. Схема получения кривой плотности распределения
Высота кривой плотности распределения показывает вероятность появления заданного значения случайной величины. Площадь под кривой плотности распределения принимается равной единице. Это вероятность появления любого значения случайной величины в диапазоне от -  до
до  . Тогда отношение площади фигуры ограниченной кривой плотности распределения и двумя вертикальными отрезками, проходящими через х' и х" к площади всей фигуры под кривой плотности распределения, равно вероятности появления очередного значения случайной величины в диапазоне от х' до х" (рис 3.3, а). В пределе х' может быть равно -
. Тогда отношение площади фигуры ограниченной кривой плотности распределения и двумя вертикальными отрезками, проходящими через х' и х" к площади всей фигуры под кривой плотности распределения, равно вероятности появления очередного значения случайной величины в диапазоне от х' до х" (рис 3.3, а). В пределе х' может быть равно -  , тогда площадь немой части фигуры будет равна вероятности появления очередного значения случайной величины меньшего или равного х" (рис 3.3, б). В случае когда х" =
, тогда площадь немой части фигуры будет равна вероятности появления очередного значения случайной величины меньшего или равного х" (рис 3.3, б). В случае когда х" =  то правая часть фигуры будет равна вероятности появления очередного значения случайной величины большего или равного х' (рис 3.3, в).
то правая часть фигуры будет равна вероятности появления очередного значения случайной величины большего или равного х' (рис 3.3, в).


|

|
Рис. 3.3. Использование кривой плотности распределения для определения вероятности появления очередного значения случайной величины в заданном диапазоне
Помимо функции плотности распределения для характеристики типа распределения может использоваться функция, показывающая вероятность появления очередного значения случайной величины меньшего или равного заданному значению. Это кумулятивная (накопленная) функция распределения. Точки на кривой распределения представляют собой значения площади под кривой плотности распределения в диапазоне от —  до х. По графику кумулятивной кривой распределения помимо вероятности появления значения случайной величины в заданных пределах, можно определить ее ожидаемое значение (такое х, для которого функция распределения равна 0,5), ожидаемый убыток (x < 0) и ожидаемый доход (x> 0). Ожидаемый убыток – это расстояние от оси ординат до центра тяжести фигуры, образованной функцией распределения и осями координат. Ожидаемый доход - это расстояние от оси ординат до центра тяжести фигуры, образованной осью ординат, функцией распределения и горизонтальной прямой, проходящей через оси ординат (рис. 3.4).
до х. По графику кумулятивной кривой распределения помимо вероятности появления значения случайной величины в заданных пределах, можно определить ее ожидаемое значение (такое х, для которого функция распределения равна 0,5), ожидаемый убыток (x < 0) и ожидаемый доход (x> 0). Ожидаемый убыток – это расстояние от оси ординат до центра тяжести фигуры, образованной функцией распределения и осями координат. Ожидаемый доход - это расстояние от оси ординат до центра тяжести фигуры, образованной осью ординат, функцией распределения и горизонтальной прямой, проходящей через оси ординат (рис. 3.4).

Рис. 3.4. Использование функции распределения для нахождения ожидаемого дохода и убытка
Типов распределения случайной величины существует очень много, но наиболее часто встречается на практике нормальное распределение. Его наибольшая распространенность доказана математически. Нормальное распределение имеет форму колоколообразной симметричной кривой, наивысшая точка которой соответствует V, и высота и ширина определяются значением  .
.
3.4 Прогнозирование с использованием регрессионной зависимости. Если известны не только значения прогнозируемой величины для объектов, аналогичных объекту прогнозирования или нми эта величина в прошлом, но и другие величины, влияющие на прогнозируемую или изменяющиеся совместно с ней, то можно говорить о наличии связи между этими величинами. Использование знаний об этой связи позволяет значительно повысить точность по сравнению с прогнозированием по выборке.
Связь между зависимой и независимой переменными может быть функциональная, в этом случае каждому значению независимой переменной соответствует одно определенное значение зависимой переменной, и вероятностная (стохастическая), когда одному значению) независимой переменной соответствует несколько значений независимой переменной с определенной вероятностью. Для описания вероятностной связи переменных используется уравнение регрессии. Оно устанавливает связь между отклонениями зависимой и независимой переменных от своих средних значений.
Наиболее часто на практике для описания связи между Х и Y применяется линейный закон. Соответственно говорят о парной линейной регрессионной зависимости, с ее помощью взаимосвязь между зависимой и независимой переменными описывается следующим образом:
y = a + 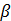 *x +
*x +  , (3.3)
, (3.3)
где.  ,
,  - коэффициенты регрессионного уравнения;
- коэффициенты регрессионного уравнения;
 - остаточный член.
- остаточный член.
Для того чтобы практически осуществлять прогнозирование с помощью регрессии, необходимо провести оценку ее параметров. Она заключается в том, чтобы определить коэффициенты  и
и  уравнения регрессии. Чаще всего это осуществляется с помощью метода наименьших квадратов. Суть его заключается в следующем. Для каждой из точек выборки записывается уравнение вида
уравнения регрессии. Чаще всего это осуществляется с помощью метода наименьших квадратов. Суть его заключается в следующем. Для каждой из точек выборки записывается уравнение вида  . Затем находится ошибка между расчетным и фактическим значениями
. Затем находится ошибка между расчетным и фактическим значениями 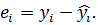 . Решение оптимизационной задачи по нахождению таких значений аи bкоторые обеспечивают минимальную сумму квадратов ошибок для всех пточек, т. е. решение задачи поиска
. Решение оптимизационной задачи по нахождению таких значений аи bкоторые обеспечивают минимальную сумму квадратов ошибок для всех пточек, т. е. решение задачи поиска
 = min, дает несмещенные и эффективные оценки коэффициентов
= min, дает несмещенные и эффективные оценки коэффициентов  иß. Следует отметить, что полученные таким образом по выборке оценки истинных значений коэффициентов регрессии для генеральной совокупности вовсе не гарантируют от ошибки при однократном применении.
иß. Следует отметить, что полученные таким образом по выборке оценки истинных значений коэффициентов регрессии для генеральной совокупности вовсе не гарантируют от ошибки при однократном применении.
Коэффициент aпоказывает значение у при х = 0, но во многих случаях х =0 не имеет смысла, кроме того, часто a < 0 также не имеет смысла, поэтому приведенной трактовкой коэффициента анужно пользоваться осторожно. Более универсальная трактовка смысла а заключается в следующем. Если a < 0, то относительное изменение независимой переменной (изменение в процентах) всегда меньше чем относительное изменение зависимой переменной. Коэффициент b показывает, на сколько единиц изменится зависимая переменная при изменении независимой переменной на одну единицу Коэффициент bчасто называют коэффициентом регрессии, подчеркивая этим, что он важнее чем а. В частности, если вместо значений зависимой и независимой переменных взять их отклонения от своих средних значений, то уравнение регрессии преобразуется к виду  .
.
Параметры уравнения регрессии говорят нам о том, как связаны между собой зависимая и независимая переменная, но ничего не говорят о степени тесноты связи, т. е. показывают положение главной оси облака данных (насколько узко или широко облако). О степени тесноты связи можно судить по линейному коэффициенту корреляции (  ). Коэффициент b корреляции меняется в пределах от -1 до +1. Чем он ближе по абсолютному значению к единице, тем сильнее зависимость. Если
). Коэффициент b корреляции меняется в пределах от -1 до +1. Чем он ближе по абсолютному значению к единице, тем сильнее зависимость. Если  < 0 то наклон линии регрессии отрицателен, чем ближе он к 0, тем слабее связь, при
< 0 то наклон линии регрессии отрицателен, чем ближе он к 0, тем слабее связь, при  = 0 линейной связи между переменными нет, а при
= 0 линейной связи между переменными нет, а при  = ǀ1ǀ связь переменных является функциональной. Коэффициент детерминации ( R2 ), который для парной линейной регрессии равен квадрату коэффициента корреляции, показывает, сколько процентов дисперсии зависимой переменной объясняется уравнением регрессии, а 1— R2 - сколько процентов дисперсии осталась необъясненной.
= ǀ1ǀ связь переменных является функциональной. Коэффициент детерминации ( R2 ), который для парной линейной регрессии равен квадрату коэффициента корреляции, показывает, сколько процентов дисперсии зависимой переменной объясняется уравнением регрессии, а 1— R2 - сколько процентов дисперсии осталась необъясненной.
Кроме этих параметров, характеризующих качество уравнения регрессии, существует и множество других. Среди важнейших из них можно отметить F-статистику и t-статистику. Первая характеризует статистическую значимость регрессионного уравнения в целом, вторая - каждого из коэффициентов, входящих в уравнение регрессии. Их значения необходимо сравнивать с табличными, которые приводятся в специальных справочниках (если фактическое значение выше табличного, значит уравнение или коэффициент статистически значимы, и наоборот).
Определив уравнение регрессии и приняв те или иные допущения относительно значения независимых переменных, можно рассчитать соответствующие прогнозные значения для исследуемого параметра.
3.5. Прогнозирование временных рядов.Временным рядом называются упорядоченные во времени значения прогнозируемой величины. На практике прогнозирование по временным рядам используется наиболее часто в силу доступности исходных данных и очевидности пути получения решения, когда имеются данные о значении прогнозируемой величины в прошлом и их необходимо продлить в будущее. Для того чтобы практически решить эту задачу часто необходимо (а иногда и достаточно) определить тенденцию изменения прогнозируемой переменной и наличие периодических (сезонных) колебаний ее значения.
Тенденция, или тренд - это долговременная закономерность изменения исследуемой величины во времени. Сезонная компонента представляет собой периодические колебания, имеющие относительно стабильный период колебаний на протяжении достаточно длительного периода времени. Более точные результаты определения тенденции достигаются в случае, если из исходного временного ряда уже удалены сезонные колебания, поэтому рассмотрим вначале методы выявления и последующего выделения сезонных колебаний. Это осуществляется с помощью аддитивной или мультипликативной модели временного ряда. Первая применяется, если амплитуда сезонных колебаний не имеет ярко выраженной тенденции к изменению во времени, в противном случае используется вторая.
Наиболее просто сезонная составляющая может быть определена с помощью метода скользящих средних с периодом осреднения равным периоду сезонных колебаний (L). Скользящая средняя - это переменная, значения которой равны среднему арифметическому значения исследуемой величины в точке, для которой она вычисляется, и значений всех точек, отстоящих от нее на 0.5*( L - 1) слева и справа в случае если L нечетное и 0.5L - если L четное. При вычислении значения скользящей средней для следующей точки временного ряда номера точек, участвующих в вычислении, смещаются на единицу. Длина периода сезонных колебаний - это число временных интервалов, через которые характер изменения временного ряда повторяется.
Схема расчета скользящей средней представлена ниже (табл. 3.1).
Дальнейшая схема определения сезонных колебаний различна для аддитивной и мультипликативной моделей. Принципиальная схема этих расчетов заключается в следующем.
Аддитивная модель. В начале находят для каждой точки временного ряда сезонные отклонения от предполагаемой тенденции, для этого:
- находятся скользящие средние с периодом усреднения равным L;
- в случае если период сезонных колебаний представляет собой четное число, то полученные скользящие средние являются межинтервальными и для получения центрированных скользящих средних осуществляется усреднение полученных средних еще раз, но на этот раз с периодом усреднения равным двум;
- для каждого интервала времени находят сезонное отклонение CKt как разность между фактическими значениями и соответствующими средними, т. е.: СКt = уt -mt.
-
Таблица 3.1
|
из
5.00
|
Обсуждение в статье: Лекция 3. МЕТОДЫ ПРОГНОЗИРОВАНИЯ СОЦИАЛЬНО- ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

