Свойства функциональных зависимостей

Эволюция понятия функции

Понятие функции может показаться вполне очевидным. Мы привыкли к записи

понимая ее как формулу, аналитическое выражение, правило и т.д. Однако у математиков не вызывает сомнения тот факт, что точность смысла этого понятия определяет построение всей математики.

В понимании сути функциональной зависимости математическая наука прошла сложный путь.

Предки Лейбница были славяне и носили фамилию Любенец.

Cлово “функция” впервые появляется в рукописях Г. Лейбница (1673 г.). Он говорит о функции как об отрезке, связанном с некоторой точкой данной кривой, выполняющем относительно нее некоторую роль.

Спустя полвека, Л. Эйлер утверждал:

“Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или количеств, провозгласив: – “Весь анализ бесконечных вращается вокруг переменных количеств и их функций”.

Еще через столетие Н. Лобачевский, существенно приблизивший понятие функции к современному пониманию, писал:

“Общее понятие требует, чтобы функцией от x называть число, которое даётся для каждого x и вместе с x постепенно изменяется”.

В 1870 году Г. Ганкель (Герман Хенкель) – крупный немецкий математик –определил функцию так:

“y называется функцией x, если каждому значению переменной величины x внутри некоторого данного интервала соответствует определенное значение y и при этом безразлично, как y зависит от x и вообще может ли эта зависимость быть выражена с помощью математических формул”.

Так что же такое функция: “число”, “переменная”, “определенное значение”, “соответствие”? Каков основной ее отличительный признак: “постоянное изменение”, “выполнимость математических действий”, “график”...?

Мы начали построение математического анализа с рассмотрения теории множеств. Именно эта основа дает возможность ввести понятие функции как одной из форм соответствия множеств, что позволяет добиться строгости и общности построения математики как единой системы знаний.

Понятие функции

Изучая множества, мы интересуемся, как правило, не природой и особенностями элементов, а их количеством, отношениями между ними. Соответствие между элементами множеств является одним из важнейших понятий в математике. При установлении, например, равенства конечных множеств или эквивалентности бесконечных множеств мы ввели «принцип» проверки взаимно однозначного соответствия их элементов.

Мы рассмотрели один из видов соответствия между множествами – взаимно однозначное соответствие. Такое соответствие не является единственно возможным. Рассмотрим другие виды соответствий.

Соответствие, при котором каждому элементу множества А указывается единственный элемент множества В, называется ОТОБРА­ЖЕНИЕМ МНОЖЕСТВААВ МНОЖЕСТВОВ. (Среди элементов множества В могут оказаться элементы, не затронутые отображением).

Если элементы множеств Аи Вобозначить точками, то примеры некоторых отображений Ав Вуказаны на рис. 8.1.

Отображение, при котором каждому элементу множества А соответствует единственный элемент в множестве В и, кроме того, каждому элементу множестваВ соответствует хотя бы один элемент множества А, называется ОТОБРАЖЕНИЕМ МНОЖЕСТВАА НА МНОЖЕСТВОВ. (Затронуты все элементы множества В).

На рис. 8.2 приведены примеры таких отображений.

Рис. 8.1. Возможные случаи отображения множества Ав множество В.

 

Рис. 8.2. Возможные случаи отображения множества Ана множество В.

Отличие друг от друга этих отображений в том, что при отображении множества А на множествоВ все элементы множества В участвуют в процедуре отображения. Когда А отображается в В, то не все элементы В могут участвовать в этой операции. Частным случаем отображения множества А на множество В является ВЗАИМНООДНОЗНАЧНОЕ СООТВЕТСТВИЕ, введенное выше (см. рис. 8.2, а и в).

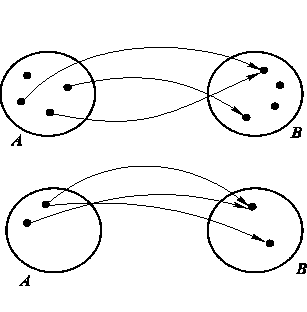Рис. 8.3. Виды соответствий, не являющихся отображениями.

А вот соответствия, которые нельзя считать отображениями (рис. 8.3). В них либо участвуют не все элементы множества А, либо один элемент множества А отображается в несколько элементов множества В.

Дадим теперь определение функции.

Пусть каждому элементу xиз множества X ставится в соответствие по некоторому закону (предписанию, правилу) f единственный элемент 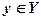. Тогда говорят, что на множестве X задана функция . Любое аналитическое задание функции обязательно предполагает наличие такого «предписания».

Запись y = f(x) впервые употребил Л.Эйлер в 1734 году.

Множество X называют областью определения функции и обозначают через . Множество значений функции обозначают через и называют областью изменения (ОБЛАСТЬЮ ЗНАЧЕНИЙ) функции.

В определении функции не существенен вопрос о числе элементов множества Х, принципиален лишь характер соответствия между элементами множеств Х и У. Множество Х может содержать и один элемент. Приведите примеры таких функций (в том числе и числовых), отражающих реальную действительность.

Соответствие между множествами X и Y является соответствием типа ОТОБРАЖЕНИЯ.

Функция может задаваться аналитически, таблично, графиком, если он существует, и иными способами. Наиболее общий способ – это отображение X в Y.

Элементы множеств Х и У могут иметь произвольную природу. Это позволяет применить теоретико-множественное толкование понятия функции к самым различным объектам и сделать его универсальной основой многих научных теорий. Математический анализ чаще всего имеет дело с числовыми множествами, поэтому функции обычно рассматриваются числовые.

Говоря о функциях, заданных на множестве действительных чисел, мы, отдавая дань уважения прошлому, сохраняем термин “функция действительного переменного”, хотя точнее было бы сказать: “функция действительного аргумента”.

Таким образом, современное представление о функциональной зависимости является соединением идей, которые формировали математический анализ, начиная со второй половины XVII века. Элемент множества Х, обозначаемый х, называется НЕЗАВИСИМОЙПЕРЕМЕННОЙ, или АРГУМЕНТОМ, а элемент множества У,обозначаемый у, – ЗАВИСИМОЙ ПЕРЕМЕННОЙ.

 

 

Свойства функциональных зависимостей

Одной из важнейших проблем математического анализа является исследование функциональных зависимостей. Выделим основные характеристики функций, подлежащие изучению.

1. ОБЛАСТИ ОПРЕДЕЛЕНИЯ И ИЗМЕНЕНИЯ ФУНКЦИИ могут быть найдены сразу или же частично оценены и в дальнейшем уточнены. Если область определения функции специально не оговорена, то функция считается заданной на ее естественной области определения, называемой ОБЛАСТЬЮ её СУЩЕСТВОВАНИЯ.

НУЛИ ФУНКЦИИ.

Они находятся из условия:

(8. 1)

Уравнение (8.1) может решаться аналитическими методами или же путем применения численных методов, которые, как правило, реализуются на ЭВМ. Более того, даже тогда, когда уравнение (8.1) удается решить точно, но это решение весьма громоздко, применяется готовое программное обеспечение для ЭВМ, позволяющее с наперед заданной степенью точности получить решение задачи. Нельзя сказать, что такое решение “хуже или лучше” точного: в реальных условиях предпочтение отдается тому способу, который позволяет получить более просто результат с заданной степенью точности. Но даже если в процессе решения уравнения (8.1) участвует ЭВМ, то остается множество проблем, требующих аналитических исследований. Например, отыскание промежутков, на которых следует ожидать корни уравнения. Сама возможность применения ЭВМ для реализации численных методов требует тончайших теоретических построений, созданных математическим анализом и пограничными науками. Поэтому при всей простоте формулировки задачи ее решение может оказаться труднейшей проблемой. Современное развитие математического анализа во многом связано с отысканием простых и удобных алгоритмов решений уравнений с использованием ЭВМ. Отдельные методы решения уравнений вида (8.1), основанные на идеях математического анализа, мы рассмотрим в дальнейшем.

ЧЕТНОСТЬ ФУНКЦИИ.

Пусть область определения функции симметрична относительно начала отсчета. Если при этом

(8. 2)

то функция называется ЧЕТНОЙ, если же

(8. 3)

то функция называется НЕЧЕТНОЙ.

В тех случаях, когда (8.2) или (8.3) не выполняется или область определения не является симметричной относительно начала отсчета, то говорят о функции ОБЩЕГО ВИДА.

Из определения четности функции следует, что график четной функции симметричен относительно оси ординат, а нечетной – относительно начала координат.

На языке логических символов четность функции означает:

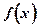–четная

(8. 4)

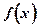–нечетная

(8. 5)

Пользуясь аппаратом математической логики, рассмотрим отрицание утверждения (8.4), то есть отрицание того, что функция – четная:

_____________

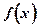–четная

Воспользуемся известными свойствами кванторных операций для предикатов

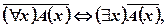(8. 6)

 

(8. 7)

и одним из законов де Моргана:

(8. 8)

Получим:

Смысл полученного результата в том, что 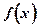не будет являться четной либо тогда, когда существуют в области определения функции такие значения x, что для любых из них противоположные им значения 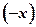не будут лежать в этой области , либо когда найдутся x такие, что . Проще говоря, функция не является четной, если ее область определения несимметрична относительно начала отсчета или же для отдельных x.

Например, функция

на отрезке [0;1] является функцией общего вида. Но эта же функция на отрезке [–1;1], как легко убедиться, является четной.

Функция

заданная на всей действительной оси, нечетна.

Для функции

вопрос о четности стоять не может, так как ее область определения 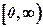несимметрична относительно начала координат.