Оценка точности и достоверности результатов выборочного наблюдения

Ошибка выборки или ошибка репрезентативности представляет собой разность соответствующих выборочных и генеральных характеристик:

Для средней количественного признака рассчитывается по следующей формуле:

;

где - выборочная средняя, 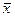- генеральная средняя

Для доли (альтернативного признака) рассчитывается по следующей формуле:

где w – выборочная доля, p - генеральная доля для альтернативного атрибутивного признака.

Ошибка выборки является случайной величиной, так как заранее неизвестно, какие единицы попадут в выборочную совокупность. Поэтому, оценивая точность результатов наблюдения, рассчитывают среднее и предельное значение этой ошибки. Эти два параметра связаны между собой( слайд 1):

;

где - предельные ошибки выборки для количественного и альтернативного атрибутивного признаков соответственно;

- средние ошибки выборки соответственно;

t – коэффициент доверия. Он зависит от вероятности, с которой гарантируется предельная ошибка выборки (доверительной вероятности).

Предельная ошибка выборки определяет предельные значения генеральной средней (доли), образующие доверительный интервал:

Предельная ошибка выборки характеризует точность результатов наблюдения, а доверительная вероятность – их достоверность. Для выборок большого объёма (не менее 30 единиц) коэффициент доверия зависит от доверительной вероятности (Р) следующим образом:

Порядок расчёта средней ошибки выборки зависит от способа выборочного наблюдения и метода отбора. При собственно-случайном наблюдении среднюю ошибку выборки определяют по формулам:

при повторном отборе

;

;

при бесповторном отборе

;

,

где 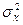- выборочная дисперсия;

n – объём выборочной совокупности;

N – объём генеральной совокупности.

Средняя ошибка бесповторного наблюдения всегда меньше средней ошибки повторного наблюдения, так как всегда выполняется условие 0 < n/N < 1.

При большом объёме выборочной совокупности механическое наблюдение близко к бесповторному собственно-случайному отбору. В этом случае применяют формулы расчёта средней ошибки бесповторной собственно-случайной выборки.

При типическом наблюдение средняя ошибка выборки составляет:

при повторном отборе

;

;

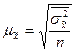при бесповторном отборе

где 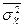- средняя из внутригрупповых выборочных дисперсий;

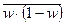- средняя из внутригрупповых выборочных дисперсий доли.

Условием применения этих формул является отбор единиц в типические группы пропорционально их числу в генеральных группах, когда:

,

где n_i, N_i – число единиц в i-ой выборочной и генеральной группах соответственно.

При серийном наблюдении для расчета средней ошибки выборки используют следующие формулы:

при повторном отборе

;

;

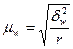при бесповторном отборе

где - межсерийная выборочная дисперсия;

- межсерийная выборочная дисперсия доли;

r - число отобранных серий;

R - число серий в генеральной совокупности.

Порядок расчёта всех видов выборочных дисперсий и взаимосвязь между ними аналогичны рассмотренны в разделе «Статистические показатели». При этом межсерийные дисперсии рассчитывают по формулам для расчета межгрупповых дисперсий. Отличие состоит в том, что все эти дисперсии рассчитывают не по генеральной совокупности, а по выборочной.