Эквивалентность определений предела функции по Гейне и по Коши

Теорема о «сжатой переменной» для последовательностей.

Теорема (принцип сжатой последовательности,).

Пусть даны последовательности и существует : : , . Известно, что . Тогда .

Док-во:Возьмем произвольный промежуток .

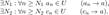
Обозначим . Тогда

Значит, .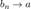

Теорема о связи бесконечно малых и бесконечно больших последовательностей.

Теорема. Последовательность { n }, n 0 является бесконечно малой последовательностью тогда и

только тогда, когда последовательность является бесконечно большой.

Доказательство следует из того факта, что неравенство 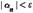равносильно неравенству

и определений бесконечно малых и бесконечно больших последовательностей.

Лемма о вложенных отрезках.

Для всякой системы вложенных отрезков

существует хотя бы одна точка c, принадлежащая всем отрезкам данной системы.

Если, кроме того, длина отрезков системы стремится к нулю: то c — единственная общая точка всех отрезков данной системы.

Доказательство:1)Существование общей точки. Множество левых концов отрезков {an} лежит на числовой прямой левее множества правых концов отрезков {bn}, поскольку

.В силу аксиомы непрерывности, существует точка c, разделяющая эти два множества, то есть

в частности .

Последнее неравенство означает, что c — общая точка всех отрезков данной системы.

2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки c и c', принадлежащие всем отрезкам системы:

.Тогда для всех номеров n выполняются неравенства: . В силу условия стремления к нулю длин отрезков для любого

для всех номеров n, начиная с некоторого будет выполняться неравенство: bn − an < E. Взяв в этом неравенстве , получим

Противоречие. Лемма доказана полностью.

Критерий Коши для последовательностей.

Последовательность { xn } назовем последовательностью Коши или фундаментальной, если

Теорема ( Критерий Коши ) Для того, чтобы последовательность { xn } сходилась, необходимо и достаточно чтобы она была фундаментальной.

Доказательство:Необходимость. Пусть {xn} сходится.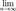

Достаточность. Пусть {xn} - фундаментальная последовательность. Докажем, что она ограничена и .

Так как последовательность фундаментальна, то , в -окресности которой сущ-ют все элементы x1,x2,x3,...,xN − 1.

Предположим, A = max{ | x1 | , | x2 | , | x3 | ,..., | xN − 1 | , | xn − ε | , | xn + ε | }. В отрезке [A, -A] содержатся все элементы последовательности, т.е. {xn} - ограниченна. В следствие теоремы Больцано-Вейерштрасса ( ) < (xn − ε;xn + ε).

в силу произвольности .

,

Эквивалентность определений предела функции по Гейне и по Коши.

Из Гейне - Коши.
Пусть lim f(x) при x->a равен A по Гейне. Выберем произвольное e>0. Предположим, что A не является пределом по Коши. Это означает, что в любой d-окрестности найдется точка, значение в которой отличается от A больше, чем на e.
Выбирая d=1,1/2,1/4 итд составим последовательность из этих точек (возможно, какая-то точка встретится в последовательности несколько раз, наплевать). У значений функции в ней не может быть предела A, потому что всеэти значения отличаются от A больше, чем на e. С другой стороны, сама она стремится к a - расстояние до a все время ограничено 1/2^n, то есть сколь угодно мало.
Тем самым получили противоречие с Гейне.
Из Коши - Гейне еще проще:
Пусть A - предел по Коши. Возьмем последовательность x_n, стремящуюся к a. Мы хотим доказать, что для достаточно больших n
f(x_n)-A будет меньше наперед заданного e. Это произойдет, как только x_n попадет в соответствующую этому e d-окрестность точки a (потому что A предел по Коши). А вся последовательность кроме конечного числа членов туда попадет, потому что стремится к a.