Порядок выполнения задания. ЛАБОРАТОРНАЯ РАБОТА № 5

ЛАБОРАТОРНАЯ РАБОТА № 5

Тема работы: Нелинейная регрессия. Выбор оптимальной степени обобщенного многочлена, аппроксимирующего экспериментальные данные.

 

Цель работы:Вычисление коэффициентов нелинейной регрессионной зависимости; подбор эмпирической формулы оптимальным образом описывающей экспериментальные данные.

 

Задание: В результате серии экспериментальных измерений получены значения в заданных точках . Величины измерены независимо друг от друга, с одинаковой среднеквадратичной ошибкой и подчиняются нормальному закону распределения; величины измерены с высокой точностью, так что погрешностью их измерения можно пренебречь.

Используя метод наименьших квадратов и ортогональные полиномы Чебышева построить регрессионную зависимость в виде обобщенного многочлена. Определить оптимальную степень многочлена. Основываясь на результатах статистического анализа обосновать оптимальность полученной эмпирической зависимости.

 

Теоретическая часть

В инженерной практике часто возникает задача подбора эмпирической формулы, адекватно описывающей имеющийся экспериментальный материал. Обычно формула строится в виде обобщенного многочлена

, (1)

где

(2)

заданная система линейно независимых базисных функций, 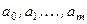- параметры формулы, являющиеся коэффициентами обобщенного многочлена. Оценки параметров, определяемые по методу наименьших квадратов, находятся из системы нормальных уравнений

,

где

, .

 

С вычислительной точки зрения наиболее целесообразным представляется использование в качестве базисных функций (2) какой-либо ортогональной (на множестве точек ) системы функций, например, полиномов Чебышева. В этом случае матрица системы нормальных уравнений становится диагональной и хорошо обусловленной. В силу этого, во-первых, чрезвычайно облегчается задача вычисления коэффициентов обобщенного многочлена, во-вторых, при последовательном уточнении эмпирической формулы на каждом этапе вычисляется лишь один новый коэффициент 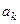, в-третьих, данный вычислительный алгоритм может быть применен при любой степени обобщенного многочлена.

Отметим, что широко используемая при полиномиальной аппроксимации система функций

,

приводящая к классическим алгебраическим многочленам, применяется лишь при . Если , то, как правило, нормальная система уравнений настолько плохо обусловлена, что вычисленные на ее основе параметры 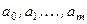оказываются полностью искаженными ошибками округления.

Ортогональные многочлены Чебышева

определяются рекуррентным соотношением

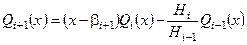
, (3)

где

.

Чтобы воспользоваться этой рекуррентной формулой, необходимо задать полиномы нулевой и первой степени; они имеют вид:

, , .

Эмпирическая формула (1) с использованием многочленов Чебышева запишется в виде

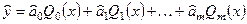. (4)

Вычисление оценок коэффициентов 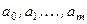и их дисперсий осуществляется по формулам:

, . (5)

Если величина известна, можно, задав определенный уровень доверительной вероятности , построить двусторонние симметричные доверительные интервалы для коэффициентов эмпирической зависимости (4):

, .

Здесь - квантиль стандартного нормального распределения. Отправным пунктом при построении данных доверительных интервалов служит тот факт, случайные величины

,

имеют стандартное нормальное распределение.

Хорошее сглаживание ошибок эксперимента при среднеквадратичной аппроксимации наблюдается когда . Но если слишком мало, то для описания сложной нелинейной зависимости коэффициентов многочлена может не хватить. Ясно, что в каждом конкретном случае должно существовать какое-то оптимальное число коэффициентов. Определяется оно следующим образом.

Задавшись некоторым числом и определив согласно (5) соответствующие коэффициенты, вычислим остаточную дисперсию

(6)

и сравним ее с известной погрешностью эксперимента по критерию Фишера. Если

, (7)

то математическая погрешность аппроксимации (значимо) больше физической погрешности исходных данных, и формула (5) нуждается в уточнении. Поэтому увеличиваем на единицу, вычисляем по формуле (5) коэффициент и повторяем проверку качества аппроксимации согласно (6), (7).

Обычно расчет начинают с , когда (при нелинейной зависимости) неравенство (7) заведомо выполнено, и последовательно увеличивают число коэффициентов до тех пор, пока при некотором значении не выполнится условие

. (8)

Это условие означает, что дисперсия (при данном ) образована только за счет случайных ошибок измерений и, следовательно, дополнительные слагаемые в функции (4) не способны эту дисперсию уменьшить. Следовательно, полученное значение является оптимальной степенью аппроксимирующего многочлена, и эмпирическая формула (4) считается окончательной. Если при этом , то вид аппроксимирующей функции (в форме обобщенного многочлена) выбран удачно, в противном случае следует поискать более подходящий вид аппроксимирующей функции.

В соотношениях (7) (8) 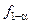- квантиль распределения Фишера, т. е. корень уравнения

, (9)

где - функция распределения Фишера с 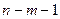и степенями свободы. Число степеней свободы числителя 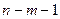равно объему выборки минус количество коэффициентов, входящих в аппроксимирующий полином; знаменателю приписываем бесконечно большое число степеней свободы (это означает, что точность измерения известна из большого числа предыдущих опытов). Величина - это уровень значимости (или вероятность ошибки 1-го рода). На практике обычно полагают . Это означает, что в пяти случаях из 100 мы можем допустить ошибку 1-го рода, т.е. отклонить гипотезу о равенстве дисперсий , когда она верна.

Следует обратить внимание, что при сравнении дисперсий по критерию Фишера в числителе должна стоять большая из сравниваемых дисперсий: если на некотором этапе расчета , то соотношения (8) и (9) записываются в виде

, .

 

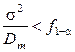Порядок выполнения задания

1. Присвойте переменной ORIGIN значение равное единице.

2. Из файлов Lab5 Nx и Lab5 Ny (N – номер варианта задания) введите исходные данные и разместите их в массивах (x) и (y).

3. Постройте полиномы Чебышева нулевого и первого порядков ( ).

4. Вычислите оценки коэффициентов , 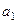и постойте согласно (4) аппроксимирующий многочлен первого порядка.

5. Постройте график линии регрессии и изобразите на нем исходные экспериментальные точки. Оцените визуально качество аппроксимации.

6. Задавшись определенным уровнем значимости и используя критерий Фишера, выясните, нуждается ли построенная регрессионная зависимость в уточнении.

7. Если уточнение необходимо, увеличьте значение на единицу; постройте многочлен Чебышева .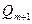

8. Вычислите очередной коэффициент и постройте обобщенный многочлен степени .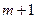

9. Последовательно повторяйте пункты 5-8 до тех пор, пока не выполнится неравенство (8).

10. Определив оптимальную степень аппроксимирующего многочлена , постройте 90-процентные доверительные интервалы для всех коэффициентов этого многочлена; убедитесь, что старшие коэффициенты многочленов более высокого порядка статистически незначимы (равны нулю). Рекомендуется построить обобщенные многочлены ( 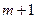) - го и ( ) - го порядков.

11. Изобразив график зависимости остаточной дисперсии от степени аппроксимирующего многочлена, проследите ее изменение.

12. Изобразите графики остатков для аппроксимирующего многочлена оптимальной степени и линейного многочлена. Что можно сказать о поведении остатков?

13. Сделайте выводы по проделанной работе.

14. Сохраните рабочий документ.