Абстрактных автоматов

ТЕОРИЯ АВТОМАТОВ.

 

Абстрактные автоматы.

 

1.1Синхронные и асинхронные автоматы.

 

 

Описание автомата использует понятие последовательности. Последовательно- сти удобно рассматривать разворачива- ющимися во времени, изменяющeмся дискретно и принимающем значения

t = 0,1,2,3, ...

 

 

Отсчёты такого времени будем называть тактами. В каждом такте будем задавать (рассматривать) значения дискретных переменных X(t),Y(t) и S(t).

 

 

 

X(t) - переменная, значения которой представляются символами входного алфавита X = {X₀, X₁, ... X_N-1} (вход-

ными символами); Y(t) - переменная
со значениями из символов выходного алфавита Y = {Y₀, Y₁, ... Y_M-1};

 

 

S(t) - переменная со значениями из символов алфавита состояний авто-
мата S = {S₀, S₁, ... S_K-1}.

Автомат осуществляет преобразова-
ния символов, потактно воспринимая входные символы X и формируя вы-

ходные - Y, а также меняя свои сос-

тояния S.

 

 

При конечности всех алфавитов автомат называется конечным, хотя он может преобразовывать последовательности бесконечной длины.

 

 

Закон, определяющий смену состояний автомата, называется функцией перехо-дов. Это функция типа:

S(t+1) = F(X(t),S(t)); (1)

либо:

S(t+1) = F(X(t+1),S(t)); (1¢)

 

 

(1) подразумевает, что смена состояния под воздействием X(t) происходит мгно-венно в самом конце такта t либо между тактами t и (t+1).

(1¢) - что воспринимая X, автомат мгно- венно, в самом начале такта меняет сос- тояние.

 

 

 

И (1), и (1¢) подразумевают, что изме- нение состояния происходит только на границах тактов, причем однократно. В самом такте изменений не происходит.

 

 

Законы, определяющие выходную реак- цию Y автомата (функция выходов), так- же могут быть разными:

 

Y(t) = F(X(t),S(t)) (2)

Y(t) = F(S(t)) (2¢)

Y(t+1) = F(X(t),S(t)) (2¢¢)

Y(t+1) = F(X(t+1),S(t)) (2¢¢¢)

 

 

Наиболее часто рассматриваются авто- маты, задаваемые функциями:

(1),(2) ; (1),(2¢) ; (1),(2¢¢) ; и (1¢),(2)

так как физическое моделирование их наиболее естественно. Однако в теории автоматов рассматриваются и варианты:

(1),(2¢¢¢) ; (1¢),(2¢) ; (1¢),(2¢¢) ; и (1¢),(2¢¢¢).

 

Иногда автоматом называют систему вида (1) либо (1¢), то-есть систему, име- ющую алфавит состояний, но не имею- щую выходной алфавит. Поведение та- кого автомата состоит в последователь- ной смене со­стояний.

 

 

 

 

С точки зрения свойств преобразований, выполняемых автоматами различных ви- дов, все они оказываются в конечном счете эквивалентными: могут представ- лять только регулярные события (см.1.2.3)

 

 

 

В то же время различные виды могут в большей или меньшей мере подходить для решения различных задач анализа и синтеза автоматов.

 

 

 

Функции переходов и выходов могут за- даваться различными способами. Чаще всего используются табличные и графо- вые способы задания.

 

 

 

Примеры табличных заданий.

	S = F(X,S)
		Y = F(X,S)

 

16 N=3 K=3 M=2

 

Одна таблица может задавать сразу и F,

и F. Например, приведенные выше таб- лицы можно свести в одну.

 

(*)

 

 

Если Y имеет вид Y=F(S), то обычно используется отмеченная таблица пе-реходов. Пример.

(**)

 

 

При графовом задании состояния S отождествляются с вершинами графа. Дуги, взвешенные (нагруженные) сим- волами Х, задают S=F(X,S).

 

 

 

Y = F(X,S) задается взвешиванием дуги.

 

 

При Y = F(S) вместо расстановки Y_j на всех дугах, выходящих из S_k , Y_j взве- шивают вершину S_k .

 

 

Графы автоматов, приведенных выше, имеют вид:

(*)

 

 

(**)

 

 

 

Функции переходов и выходов могут иметь область определения , меньшую по сравнению со всеми возможными наборами значений их аргументов. При этом мы имеем недоопределенные (частичные) автоматы.

 

 

 

Зная функции переходов и выходов, можно описать поведение автомата, воспринимающего некоторую вход-
ную последовательность, если извест-
но состояние, в котором находился автомат в такт появления первого символа входной последовательности.

 

Примеры.

1. Пусть S(t+1) = F(X(t),S(t)) и Y(t) =
= F(X(t),S(t)) заданы, как (*). Полагая, что S(t) = S₀ , рассмотрим поведение автомата на X₀ X₀ X₁ X₂ ...

 

2. Пусть S(t+1) = F(X(t),S(t)) и Y(t) =
= F(S(t)) заданы, как (**). Полагая, что S(t) = S₀ , опишем поведение ав- томата на X₁ X₂ X₂ X₀ ...

 

 

 

Говоря об автоматах, мы предполагаем возможность использования их для описания либо реализации преобра- зований дискретной информации.

 

При этом подразумевается наличие системы договоренностей (интер- претации), по которой можно уста-

новить соответствие реального вре-
мени тактам автомата.

 

 

 

При интерпретации нужно на полуоси времени выделить интервалы с номе- рами 0,1,2, ... , задающие такты авто- мата:

 

 

Длительности тактов (и пауз между

ними) могут быть любыми, вплоть

до одного момента времени. Способы разметки времени также могут быть разными; мы выделим 2 из них, опре- деляющие различные классы автоматов.

 

 

 

С этой целью будем рассматривать

автомат как объект, который обмени- вается входными и выходными сиг-

налами (представляющими символы входного и выходного алфавита) с вне- шней средой.

 

 

 

 

 

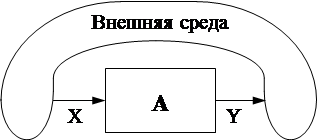Такты можно выделить с помощью некоторых «часов» (датчика тактов), общих как для автомата, так и для «внешней среды», например, в виде генератора синхроимпульсов, сигнали- зирующего о наличии такта.

 

 

Автоматы, работающие в такой системе тактности, называются синхронными.

Таким образом, в синхронном автомате

X и Y должны формироваться в опре- деленное время, выделяемое датчиком тактов.

 

 

Физическая модель может интерпрети- роваться как синхронный автомат, на- пример, следующим образом.

Имеем генератор СИ , который выде- ляет на полуоси времени интервалы Т.

 

 

Пусть во время этих интервалов вход- ные воздействия Х и выходные реакции

Y физической модели, а также внутрен- ние сигналы, представляющие состояния

S, не изменяются (смена X,Y и S проис- ходит только между интервалами Т).

 

 

В этом случае интервалы Т соответ-

ствуют тактам. Если поведение физи- ческой модели при этом можно описать функциями переходов и выходов, то физическая модель может рассматри- ваться как автомат.

 

 

 

Зафиксируем временную диаграмму функционирования рассматриваемой физической модели:

 

 

 

 

 

 

Для синхронных автоматов наиболее естественны и наиболее употребимы задания вида:

 

 

 

I обычно называют автоматом Мили,

 

II - автоматом Мура;

 

III будем называть автоматом Мили с

задержкой.

 

 

Можно искать интерпретацию, при ко- торой некоторое физическое устройство может рассматриваться (описываться) как автомат. Это задача анализа.

 

 

 

 

Можно строить физическую модель, которую при определенной интерпре- тации можно считать автоматом с тре- буемым законом функционирования. Это задача синтеза.

 

 

Выделять такты с помощью генератора синхроимпульсов (СИ) можно по раз- ному (для разных физических моделей могут быть удобными разные интер- претации):

 

 

 

 

 

 

В асинхронных автоматах начало (и ко- нец) тактов определяется по факту из- менения Х на входе автомата.

Паузы между тактами представлены
моментами смен Х.

 

 

Таким образом, для асинхронных авто- матов такт формируется внешней сре- дой (X и Y в асинхронном автомате мо- гут формироваться в произвольное вре- мя).

 

 

Изменение X(t) для асинхронного авто- мата означает начало следующего такта (t+1). Новое значение X(t+1) рассмат- ривается как причина изменения состо- яния S(t) и появления нового S(t+1).

S(t+1) появляется как реакция на X(t+1) сразу же: S(t+1) = F( X(t+1), S(t)).

 

 

 

Функции переходов такого вида пред- ставляют наибольший интерес из-за трудностей физического моделирова- ния асинхронных автоматов с S(t+1) =

= F( X(t), S(t)).

Функции выходов обычно имеют вид:

Y(t) = F( X(t), S(t)) , либо

Y(t) = F(S(t)).

 

 

В итоге мы имеем:

 

 

В заключение отметим, что и в син-

хронных, и в асинхронных автоматах

чаще всего мы имеем дело с иници- альными автоматами, то есть с такими, для которых заданы начальные состо- яния S(0).

 

Задачи теории

абстрактных автоматов.

 

Эквивалентность

Автоматов.

 

 

Наибольший интерес для нас предста- вляют абстрактные синхронные авто- маты Мили и Мура, которые мы и бу- дем рассматривать.

 

 

Пусть мы имеем автомат Мили

 

t = 0,1,2, ...

S(0) = S₀ .

 

Входная последовательность X(0) X(1) X(2)... будет отображаться таким авто- матом в выходную Y(0) Y(1) Y(2)...

Получаемое соответствие называется отображением, индуцируемым рассма- триваемым автоматом Мили.

 

 

Если устанавливать связь выходной ре- акции автомата Мура с выходной пос- ледовательностью, то можно установить

ее так:

Y(t) = F(S(t)) заменим на Y(t+1) =

= F(S(t+1)) = F(F(X(t),S(t))) =

= Y(X(t),S(t)).

 

 

 

 

Отсюда видно, что автомат Мура мож- но рассматривать как автомат Мили со сдвинутой на такт выходной реакцией.

 

 

 

Отображение, индуцируемое автоматом Мура , устанавливает соответствие X(0) X(1) X(2)... и Y(1) Y(2) Y(3)... , так как Y(0) - значение, не зависящее от вход- ной последовательности автомата Мура.

 

Автоматы Мура можно считать част-

ным случаем автоматов Мили, если нас интересует не истинное время появле- ния выходных символов Y, а лишь по- рядок их следования во времени (отоб- ражение Х в Y).

 

 

 

В абстрактной теории автоматов, испо- льзующей лишь свойства индуцируемых отображений, автоматы Мура так и трактуются. При изучении же способов построения композиций автоматов (в структурной теории) автоматы Мура рассматриваются как отдельный класс.

 

 

Автоматы (в том числе и разных видов) называются эквивалентными , если ин- дуцируемые ими отображения одина- ковы.

 

 

 

Можно доказать, что:

для любого автомата Мура можно

построить эквивалентный автомат

Мили (и наоборот).

 

Частным случаем эквивалентности ав- томатов одного вида является их равен-ство.

Автомат А вкладывается в автомат В, если функции переходов и выходов А в области их определения равны функци- ям переходов и выходов автомата B.

 

 

 

При этом А называется подавтоматом В,

а В - надавтоматом А (обозначается А Í

Í В). Если А Í В и В Í А, то автоматы равны : А = В.

 

 

A

A Í B

B

Пример.

 

 

 

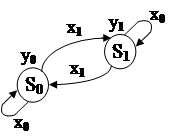
Обобщая равенство функций переходов

и выходов до равенства с точностью до переименования символов, можно гово- рить не о вложении, а об изоморфном вложении автоматов и соответственно

не о равных, а об изоморфных автома- тах.

 

Пример

 

Автомат С изоморфен автомату А из предыдущего примера. С изоморфно вкладывается в В.