В а) автоматы разных подмножеств

не могут обмениваться сигналами ни

в каком такте из-за несовместимости

их входных и выходных микротактов.

 

 

 

 

В б) существуют такты, в

которых входные и выходные

микротакты автоматов разных

подмножеств совместимы, что

позволяет передавать между

ними сигналы.

 

 

Пример

 

 

Возможное выделение сопрягаемых микротактов

 

 

3. Композиции согласованных автоматов.

Согласованным называется автомат , входной микротакт которого опре-

Деляется сигналами извне, а выход-

Ной микротакт - сигналами самого

Автомата.

 

 

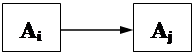В композиции

 

сигналы, определяющие выходной мик-

ротакт А_i, одновременно определяют

входной микротакт А_j.

Такие композиции могут строится из автоматов с разной инерционностью (скоростью) работы.

 

 

В асинхронных согласованных автома-

тах, называемых апериодическими , длительность периода каждого такта

будет определяться скоростными свой-

ствами конкретных автоматов компози-

ции. (Внешняя среда при этом рассмат-

ривается как автомат композиции.)

 

Чаще всего мы рассматриваем компо-зиции синхронных автоматов с единой системой тактности либо композиции синхронных автоматов с сопрягаемыми системами тактов.

 

 

Композиция - автомат, если:

для каждого автомата А_i композиции в любом его входном микротакте (и вы- ходном) на любом его входе (и выходе) присутствует сигнал, однозначно задающий некоторый символ из его алфавита.

 

Данное условие подразумевает:

1) необходимость отождествления всех элементарных входов и выходов;

2) недопустимость отождествления входа и выхода при несовпадении входных микротактов с соответству-ющими выходными;

 

3) недопустимость отождествления двух и более выходов;

4) недопустимость соединений, дающих в композиции «порочные петли ».

 

Условия 1¸3 очевидны.

Условие 4 рассмотрим отдельно.

 

 

« Порочной петлей » называется кольцо автоматов А₁, А₂, ... А_Р,

 

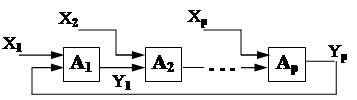для которого не существует единственного

решения системы

 

« Порочная петля » возможна, если в

кольце все автоматы - автоматы Мили.

 

Пример

 

 

X1 = 1 , X2 = 1

139

Пусть А1 - в состоянии S1, А2 - в состоянии S2, и пусть

Y₁ (S₁ , X₁ = 1, Z₁ ) = ₁

Y₂ (S₂ , X₂ = 1, Z₂ ) = Z₂ .

 

Тогда Y₁ = ₁ ; Z₂ = Y₁ = ₁ ;

Y₂ = Z₂ = ₁ ; Z₁ = Y₂ = Z₂ = ₁

 

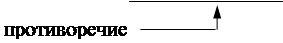140 Решения нет.

Для кольца синхронных автоматов

Мили и Мура с произвольными закона-

ми функционирования « порочная петля » отсутствует , если в кольце есть хотя бы

один автомат Мура.

 

 

Так как для автоматов Мура Y(t) = F( S(t) ), то-есть Y(t) ¹ F( X(t) ), то появление нового X(t) не изменит Y(t).

При определенных условиях можно иметь кольцо из автоматов Мили, не образующих «порочную петлю».

 

 

Возможно это, если в любом такте хотя бы

один автомат кольца А_j получает Х_j , при котором Y_j =F(X_j , S_j) = F(S_j) , то-есть имеем

в данном такте функцию выходов того же

вида, что и автомат Мура.

 

 

Следует отметить, что часто использу- ются композиции автоматов с «пороч- ными петлями» , но при таких дисцип- линах смен входных сигналов, при ко- торых в любом такте в кольце есть хотя бы один автомат с Y ¹ F(X).