Производная и ее приложения

Производная. Понятие производной является одним из важнейших в курсе математики. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.

Производной функции y=f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

 

Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.

Если у=f(u) и u=φ(x)— дифференцируемые функции своих аргумен­тов, то производная сложной функции у=f(φ(x)) существует и равна произ­ведению производной функции у по промежуточному аргументу u на произ­водную промежуточного аргумента u по независимой переменной х:

 

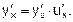Аналогичная формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более.

Таблица формул дифференцирования

1. с’=0

2. х’=1

3. (u±v)’ = u’ ± v’

4. (uv)’ = uv’ + vu’

5. (cu)’ = cu’

6.

7.

8.

9.

10. (a^u)’ = a^u ln a • u’

11. (e^u)’ = e^u ln eu’ = e^uu’

12. где u>0

13. где u>0

14. (sin u)’ = cos u • u’

15. (cos u)’ = - sin u • u’

16.

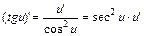
17.

18.

19.

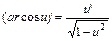
20.

 

21.

Здесь u и v — дифференцируемые функции от х, а

с - постоянная величина.

Пример 1. Найти производную функции

Решение. Дифференцируем функцию по формулам

Пример 2. Найти производную функции у=sin³j и вычислить ее значе­ние при j= p/3.

Решение. Это сложная функция с промежуточным аргументом sinj. Дифференцируем ее по формулам

(uⁿ)' = nu^n-1u', (sin u)' = cos u • u':

f(j) = 3 sin²j (sinj)' = 3 sin²j cosj.

 

Вычислим значение производной при j = p/З:

f(p/3) = 3sin² (p/3) cos(p/3)=3(Ö3/2)² •(1/2)=3•(3/4) • (1/2)=9/8.

Пример 3. Найти производную функции

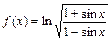
Решение. Сначала преобразуем функцию, используя свойства лога­рифмов: t

Дифференцируя, получим

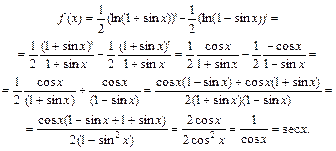
Геометрический смысл производной. Производная функции у =f(x) представляет собой угловой коэффициент касательной, проведенной к графику функции в любой его точке.

Угловой коэффициент касательной, проведенной к графику функции y=f(х) в точке A(а;b), равен значению производной функции при х = а:

k_кас=y'(a)=f'(a).

Уравнение касательной, проведенной к графику функции в этой точке, имеет вид

у— b=k (х -а), где k=f’(a).

Пример 4.Составить уравнение касательной, проведенной к графику функции в точке с абсциссой х=2.

Решение. Сначала найдем ординату точки касания А (2;у). Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кри­вой, т. е.

 

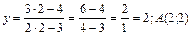
Уравнение касательной, проведенной к кривой в точке А(2;2), имеет вид у - 2 = k(x - 2). Для нахождения углового коэффициента касательной найдем производную:

 

Угловой коэффициент касательной равен значению производной функции при х = 2:

Уравнение касательной таково:

у - 2 = - (х - 2), или у - 2 = -х + 2, т. е. х + у - 4 = 0.

 

Физический смысл производной. Если тело движется по прямой по за­кону s = s (t), то производная пути s по времени t равна скорости движения тела в данный момент времени t:

Быстрота протекания физических, химических и других процессов также выражается с помощью производной.

Производная функции у=f(х) равна скорости изменения этой функции при данном значении аргумента х:

 

Пример 5. Закон движения точки по прямой задан формулой s=t²+3t+5. В какие моменты времени t скорость движения точки равна нулю?

Решение. Скорость прямолинейного движения точки равна производ­ной пути s по времени t:

v (t) = s' = 3 t² - 6t + 3; v (t) =0,З t² - 6t + 3 = 0,

t² - 2t + 1 = 0, (t — 1)² = 0, откуда t = 1.

Вторая производная. Производной второго порядка (или второй про­изводной) функции называется производная от первой производной у' =f' (х):

у" = (у’)' или f" (х) = (f' (х))'.

Пример 6. Найти вторую производную функции f(x)=tg x.

Решение. Сначала по формуле найдем первую произ­водную:

Дифференцируя еще раз по формулам (uⁿ)’=nu^n-1u’, сos u)’=-sin u*u’, найдем вторую производную:

 

 

 

Физический смысл второй производной. Если тело движется прямоли­нейно по закону s=s(t), то вторая производная пути s по времени t равна ускорению движения тела в данный момент времени t:

а (t) = v' = s".

Пример 7. Точка движется по прямой по закону s=t³-5t²+8t+2. (s - в метрах, t - в секундах). Найти ускорение движения точки в конце второй секунды.

Решение. Сначала найдем производную пути s по времени t:

s' = 3 t² - 10 t + 8.

Ускорение прямолинейного движения точки равно второй производной пути s по времени t:

а (t) = s" = 6 t - 10, а(2) = 6 • 2 - 10 = 12 - 10 = 2.

Ускорение движения точки в конце второй секунды равно 2 м/с².

 

Приложения производной к исследованию функций.Дифференцируе­мая функция у=f (х) возрастает на промежутке ]а, b[, если ее производная положительна в каждой точке этого промежутка.

Дифференцируемая функция у=f(x) убывает на промежутке]а; b[, если ее производная отрицательна в каждой точке этого промежутка.

Функция y=f(x) имеет максимум в точке х = x₁ (рис. 38), если для всех значений х, достаточно близких к x₁, выполняется неравенство f(х) < f(х₁); x=х₁ - точка максимума; у_maх =f (х₁) - максимум функции.

Функция у = f(x) имеет минимум в точке х = х₂ (рис. 38), если для всех значений х, достаточно близких к х₂, выполняется неравенство f(x) > f(х₂); х = х₂ - точка минимума; у_maх = f(х₂) - минимум функции.

Точки максимума и минимума называются точками экстремума, а значе­ния функции в этих точках - экстремальными.

Точки, в которых производная функции обращается в нуль, называются критическими, точками I рода.

Первое достаточное условие существования экстре­мума функции. Если при переходе через критическую точку I рода х=х₀ производная функции y=f(х) меняет знак, то х=х₀ - точка

 

 

экстремума.

При этом если производная меняет знак с плюса на минус, то х=х₀= - точка максимума, а у_mах =f(х₀). Если же производная меняет знак с минуса на плюс, то х= х₀ - точка минимума, a у_min =f(х₀)

Второе достаточное условие существования экстре­мума функции. Если в точке х = х₀ первая производная функции у=f(x) обращается в нуль, а вторая производная отлична от нуля, то х=х₀ - точка экстремума.

При этом если вторая производная в этой точке положительна (f" (х₀)>0), то х=х₀ - точка минимума; если вторая производная в этой точке отрица­тельна (f"(х₀) < 0), то х= х₀ – точка максимума.

рис. 38.

 

Направление вогнутости и точки перегиба кривой. Говорят, что на промежутке ]а, b[ кривая обращена выпуклостью вверх или вы­пукла (Ç), если она лежит ниже касательной, проведенной в любой ее точке (рис. 42).

Говорят, что кривая на промежутке ]b,с[ обращена выпуклостью вниз или вогнута (È), если она лежит выше касательной, проведенной в любой ее точке (рис. 42).

Точка А, в которой меняется направление вогнутости кривой, называется точкой перегиба кривой (рис. 42).

График дифференцируемой функции y=f(x) является выпуклым на про­межутке ]а; b[, если вторая производная функции отрицательна в каждой точке этого промежутка.

График дифференцируемой функции y=f(x) является вогнутым на про­межутке ]b; с[, если вторая производная функции положительна в каждой точке этого промежутка.

Точки, в которых вторая производная функции обращается в нуль, назы­ваются критическими точками II рода.

Если при переходе через критическую точку II рода х = х₀ вторая произ­водная функция меняет знак, то х = х₀ - абсцисса точки перегиба. Ордината точки перегиба равна значению

 

 

функции в точке х₀, т.е. у_т.п. =f(х₀); А(х₀;f(х₀)) - точка перегиба графика функции у = f(х).

Исследование функций и построение их графиков. Исследование функции можно проводить по следующей схеме:

1. Найти область определения функции.

2. Найти точки пересечения графика функции с осями координат.

3. Найти промежутки монотонности и экстремумы функции.

4. Найти направление вогнутости и точки перегиба графика функции.

5. Для уточнения графика функции рекомендуется найти несколько допол­нительных точек из уравнения функции.

Пример 8. Построить график функции у = х³ - Зх.

Решение 1. Областью определения функции служит множество всех действительных чисел, т. е. х = R.

2. Находим точки пересечения графика функции с осями координат:

рис.42.	рис. 43.

 

 

3. Находим экстремумы функции. Для этого сначала найдем производную у' = Зх² - 3. Затем найдем критические точки I рода: у' = 0,Зх² - 3=0, х² = 1, х₁= 1, х₂ = -1. Отметим эти точки на числовой прямой (рис. 43). Исследуем знак производной в каждом интервале; у'(-2) > 0, у' (0) < 0, у'(2) > 0. Функция возрастает при хÎ] -¥,-1[U]1,+¥[и убывает при хÎ] –1,1[. Итак, х= -1 — точка максимума; у_maх = у(-1)=(-1)³-3(-1)=-1+3=2; х=1 — точка минимума; y_min = у (1) = 1³—3*1=1-3=-2.

 

4. Находим направление вогнутости и точки перегиба графика функции. Для этого сначала найдем вторую производную у" = 6х, а затем критические точки II рода: у" =0,6х=0, х = 0. Отметим эту точку на числовой прямой (рис. 44). Исследуем знак второй производной в каждом интервале:

у"(-1) < 0, у"(1)>0.

рис. 44	рис. 45

 

Таким образом, график является выпуклым при хÎ] -¥,0[ и вогнутым при хÎ] 0, + ¥ [; х = 0 — абсцисса точки перегиба, y_т.п= у(0) = 0; О (0,0) - точка перегиба графика функции.

Отметим все полученные точки в сис­теме координат и соединим их плавной кривой (рис. 45).

Для уточнения графика функции можно найти дополнительные точки, используя уравнение функции: у(-2)= -2, у (2) =2.

 

Вопросы для самопроверки

1. Дайте определение производной функции.

2. В чем состоит геометрический смысл производной?

3. В чем состоит физический смысл производной?

4. Дайте определение второй производной функции.

5. В чем состоит физический смысл второй производной?

6. Напишите все формулы дифференцирования.

7. Как найти промежутки возрастания и убывания функции?

8. Как найти точки экстремума и экстремумы функции?

9. Как найти промежутки выпуклости и вогнутости кривой?

10. Как найти точки перегиба кривой?

 

 

11. Найдите производные функций: а) у = In tg (х/2);

б) у = cos² Öx; в) f(x)=(x+1)2х-1.

12. Составьте уравнение касательной к кривой у = х² — 4х в точке с абсциссой х = 1.

13. Прямолинейное движение точки задано уравнением

(s - в метрах, t - в секундах). Найдите скорость и ускорение движения точки в конце второй секунды,

14. Какой из прямоугольников с периметром, равным 48см, имеет наибольшую площадь?

15. Число 66 представьте в виде суммы двух положительных слагаемых так, чтобы произведение этих чисел было наибольшим.

 

Ответы. 11. a) cosec х; б) в)

12. 2х+у+1=0. 13. 3 м/с, 2 м/с². 14. Квадрат со стороной 12 см. 15. 33 и 33.

 

Решение. Находим производную данной функции, используя формулы

 

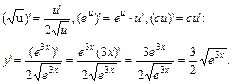
Умножив производную на дифференциал аргумента, получим дифференциал:

Пример 2. Вычислить значение дифференциала функции n = In sin 2j при j = p/8, Dj = 0,02.

Решение: Дифференциал функции вычисляем по формуле dv = v' (j) dj.

 

 

Прежде чем применить эту формулу, используя равенства

(sin u)’ = cos u^,u’, (си)’=си’, находим производную функции и ее значение при j = p/8:

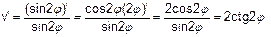
Понятие о дифференциальном уравнении. Дифференциальным уравне­нием называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции).

Если дифференциальное уравнение содержит производную или дифферен­циал не выше первого порядка, то оно называется дифференциальным урав­нением первого порядка. Общий вид такого уравнения F (х, у, у') = 0.

Общим решением дифференциального уравнения первого порядка назы­вается функция у = j(х, С) от х и произвольной постоянной С, обращающая это уравнение в тождество.

Общее решение, записанное в неявном виде Ф (х, у. С) =0, называется общим интегралом.

Частным решением уравнения F (х, у, у') = 0 называется решение, полу­ченное из общего решения при фиксированном значении С: у =j(х, С_о), где С_о - фиксированное число.

Частным интегралом уравнения F(x, у, у') = 0 называется интеграл, полученный из общего интеграла при фиксированном значении С: Ф (х, у, С_о) = 0.

График любого частного решения дифференциального уравнения F (х, у, у') = 0 называется интегральной кривой. Общему решению (и общему ин­тегралу) этого уравнения соответствует семейство интегральных кривых, зави­сящих от одного параметра С.

Пример 1. Составить уравнение кривой y=f(x), если угловой коэффи­циент касательной, проведенной в любой точке кривой, равен 2х.

Решение. Так как на основании геометрического смысла производной у' = k_кас, то получим дифференциальное уравнение первого порядка:

Чтобы найти, искомую функцию у=f(х), надо проинтегрировать обе час­ти уравнения: òdy = ò 2xdx. Отсюда получим общее решение дифференциаль­ного уравнения:

 

 

у=х²+С. Геометрически это решение представляет собой семейство парабол (рис. 55) с вершиной на оси Оу, симметричных относитель­но этой оси.

Чтобы из общего решения выделить частное решение, надо задать началь­ные условия. Пусть у = -1 при х=1; тогда общее решение примет вид -1 = 1 + С, откуда С = - 2. Геометрически частное решение у = х² - 2 представляет со­бой параболу, проходящую через точку (1; -1) (рис. 55).

 

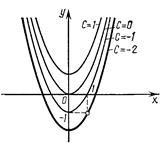
рис. 55

Дифференциальные уравнения с раз­деляющимися переменными. Общий вид такого уравнения

Х (х) • Y (y)dx + X₁(x) • Y₁ (у) • dy = 0,

где Х (х), Х₁(х) — функции только от х, Y(у), Y₁(у)—функции только от у.

Поделив обе части уравнения на произве­дение X₁(x)•Y(у)¹0, получим уравнение с разделенными переменными: