 |
Главная |
Задача № 3. Нахождение максимума и минимума функции
|
из
5.00
|
3.1. Найдите интервалы монотонности и экстремум функции 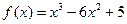 .
.
 Функция определена на всей числовой оси. Найдём её производную.
Функция определена на всей числовой оси. Найдём её производную. 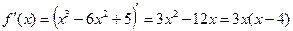 .
.
Найдём критические точки, приравняв производную к нулю.
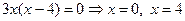 — критические. Результаты исследования занесём в таблицу:
— критические. Результаты исследования занесём в таблицу:
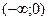
| 
| 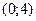
| 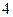
| 
| |
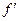
| + | 
| 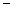
| 
| + |

| 
| 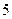
| 
| 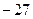
| 
|
 Таким образом, функция
Таким образом, функция 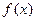 возрастает а интервалах
возрастает а интервалах 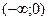 и
и  , а убывает на интервале
, а убывает на интервале 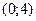 .
.
Точки 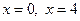 являются точками экстремума. В точке
являются точками экстремума. В точке 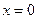 функция достигает максимума, в точке
функция достигает максимума, в точке 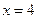 функция достигает минимума.
функция достигает минимума.
3.2. Найдите наибольшее и наименьшее значения функции 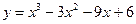 на отрезке
на отрезке 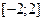 .
.
 Находим критические точки данной функции.
Находим критические точки данной функции.
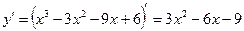 .
.
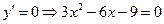 ;
;
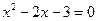 ;
;
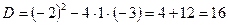 ;
;
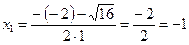 ;
;
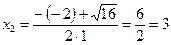
Отрезку 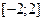 принадлежит только одна критическая точка
принадлежит только одна критическая точка  . Вычисляем значения функции в этой точке и на концах отрезка:
. Вычисляем значения функции в этой точке и на концах отрезка:
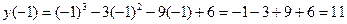 ;
;
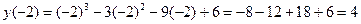 ;
;
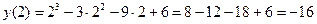 .
.
Сравнивая полученные значения, найдем, что 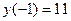 есть наибольшее значение функции, а
есть наибольшее значение функции, а 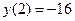 — наименьшее значение функции на отрезке
— наименьшее значение функции на отрезке 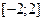 .
.
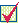
 3.3. Найти максимум и минимум функции
3.3. Найти максимум и минимум функции 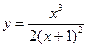 .
.
1. Функция определена для всех 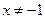 , т.е. область определения
, т.е. область определения  .
.
Находятся точки экстремума функции, вычисляются её экстремальные значения, находятся интервалы монотонности функции.
2. 
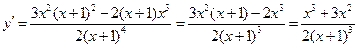 .
.
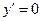 при
при 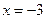 и
и 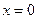 .
.
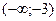
| 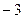
| 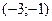
| 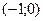
| 
| 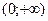
| |
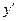
| + | 
| 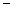
| + | 
| + |
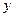
| 
| 
| 
| 
| 
| 
|
Поэтому функция возрастает в интервалах 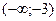 и
и 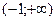 , убывает в интервале
, убывает в интервале 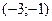 . Точка
. Точка 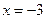 является точкой максимума и
является точкой максимума и 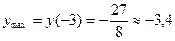 .
.
Тема "Дифференциальное исчисление функций нескольких переменных"
Задача 1. Линии уровня функции двух переменных.
Для функции 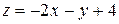 построить график и линии уровня. Записать уравнение линии уровня, проходящей через точку
построить график и линии уровня. Записать уравнение линии уровня, проходящей через точку 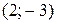 .
.
Решение
Графиком линейной функции двух переменных 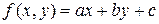 является плоскость в пространстве. График данной функции
является плоскость в пространстве. График данной функции 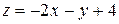 представляет собой плоскость, проходящую через точки
представляет собой плоскость, проходящую через точки 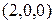 ,
, 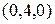 ,
, 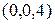 .
.
Линиями уровня 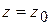 функции
функции 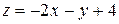 являются прямые
являются прямые 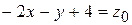 , или
, или 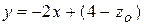 . Они параллельны друг другу и отсекают на оси
. Они параллельны друг другу и отсекают на оси 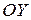 отрезок
отрезок 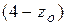 .
.
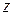
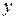
 4
4
4 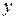
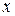 0 1 2
0 1 2 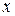
Рисунок 3 – График функции 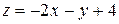
Рисунок 4 – Линии уровня функции
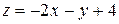
Задача 2. Вычисление частных производных функций.
Даны функции двух переменных 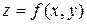 .
.
1) Для функции 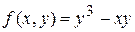 найти частные производные
найти частные производные 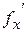 ,
, 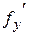 и вычислить их значения в точке
и вычислить их значения в точке 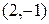 .
.
2) Для функции 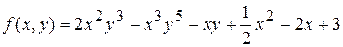 показать, что
показать, что 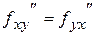 .
.
Решение
1) Частная производная функции 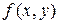 по переменной
по переменной 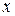 находится в предположении, что
находится в предположении, что 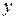 постоянна:
постоянна:
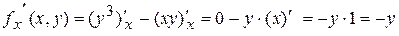 .
.
Частная производная функции 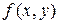 по переменной
по переменной 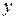 находится в предположении, что переменная
находится в предположении, что переменная 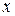 постоянна:
постоянна:
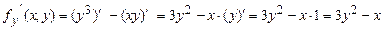 .
.
Вычислим значения частных производных при  ,
, 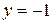 :
:
 ,
, 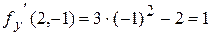 .
.
2) Смешанная частная производная второго порядка 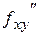 находится последовательным дифференцированием сначала исходной функции
находится последовательным дифференцированием сначала исходной функции 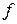 по
по 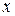 (считая
(считая 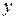 постоянным), затем дифференцированием производной
постоянным), затем дифференцированием производной 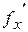 по
по 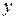 (считая
(считая 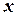 постоянным):
постоянным):
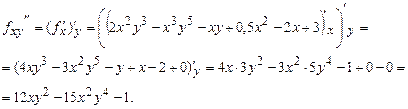
Производная 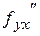 находится последовательным дифференцированием функции
находится последовательным дифференцированием функции 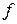 сначала по
сначала по 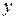 , затем производной
, затем производной 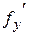 по
по 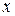 .
.
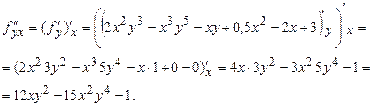
Как и следовало ожидать, 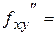
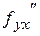 .
.
Задача 3. Градиент функции двух переменных.
Дана функция 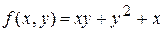 .
.
1) Найти градиент 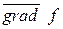 в точке
в точке  .
.
2) Найти и построить 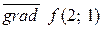 в точке
в точке 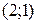 .
.
Решение
1) Градиент - это вектор, координаты которого равны частным производным функции по переменным 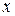 и
и 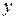 :
:
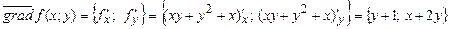 .
.
2) В точке 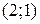 градиент
градиент 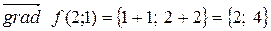 . Начало вектора
. Начало вектора 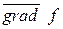 в точке
в точке 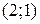 , а конец - в точке
, а конец - в точке  .
.
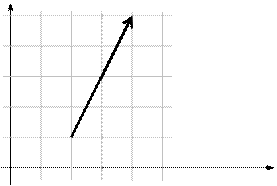
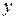
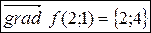
0 2 4 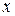
Рисунок 5 – Градиент функции
Задача 4. Нахождение наибольшего и наименьшего значений функции в области.
Найти графическим методом наибольшее и наименьшее значения функции 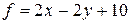 в области, заданной системой линейных неравенств:
в области, заданной системой линейных неравенств:
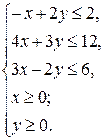
Решение
1. Построим полуплоскости и найдем их пересечение. В качестве контрольной точки возьмем 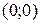 , не лежащую на граничных прямых.
, не лежащую на граничных прямых.

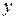
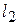
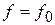
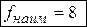
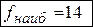

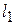
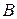
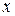
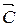
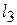
Рисунок 6 – Графическое решение задачи нахождение наибольшего и наименьшего значений функции
Прямая ( 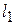 )
) 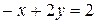 построена по точкам
построена по точкам 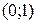 и
и 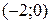 . Так как неравенство
. Так как неравенство 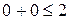 верное, то полуплоскость обращена в сторону точки
верное, то полуплоскость обращена в сторону точки 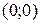 .
.
Прямую ( 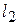 )
) 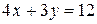 строим по точкам
строим по точкам 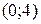 и
и 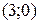 . Неравенство
. Неравенство 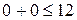 верное, полуплоскость направлена в сторону
верное, полуплоскость направлена в сторону 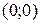 .
.
Прямая ( 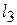 )
) 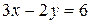 построена по точкам
построена по точкам 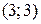 и
и 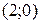 ; полуплоскость обращена в сторону
; полуплоскость обращена в сторону 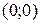 .
.
Неравенства 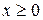 и
и 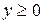 показывают, что пересечение полуплоскостей находится в первой координатной четверти.
показывают, что пересечение полуплоскостей находится в первой координатной четверти.
2. Построим градиент функции 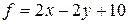 - вектор с координатами
- вектор с координатами 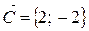 , а перпендикулярно градиенту - линию уровня, прямую
, а перпендикулярно градиенту - линию уровня, прямую 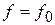 .
.
Параллельным переносом линии уровня 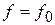 в направлении градиента найдем точку ее «входа» в область – это точка
в направлении градиента найдем точку ее «входа» в область – это точка 
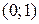 на оси ОУ, в которой функция принимает наименьшее значение. Вычислим значение функции в этой точке:
на оси ОУ, в которой функция принимает наименьшее значение. Вычислим значение функции в этой точке: 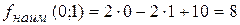 .
.
Продолжая движение линии уровня в направлении градиента 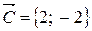 , найдем точку
, найдем точку 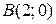 «выхода» линии уровня из области, в которой функция принимает наибольшее значение. Вычислим значение функции в этой точке:
«выхода» линии уровня из области, в которой функция принимает наибольшее значение. Вычислим значение функции в этой точке:  .
.
Ответ:  ,
, 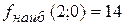 .
.
|
из
5.00
|
Обсуждение в статье: Задача № 3. Нахождение максимума и минимума функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

