 |
Главная |
К разделу: «Элементы линейной алгебры анализа»
|
из
5.00
|
| К главе I. | |
| 1) | Если матрицы  и и 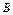 можно умножать, следует ли из этого, что их можно складывать? можно умножать, следует ли из этого, что их можно складывать?
|
| 2) | Если матрицы 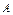 и и 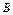 можно складывать, следует ли из этого, что их можно умножать? можно складывать, следует ли из этого, что их можно умножать?
|
| 3) | Можно ли умножать квадратную матрицу на не квадратную? |
| 4) | Может ли произведение не квадратных матриц быть квадратной матрицей? |
| 5) | Может ли при умножении нулевых матриц получиться нулевая матрица? |
| 6) | Могут ли совпадать матрицы 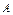 и и  ? ?
|
| 7) | Как выглядит матрица  ? ?
|
| 8) | Верно ли равенство  ? ?
|
| 9) | Верно ли равенство 
|
| 10) | Верно ли равенство 
|
| 11) | Верно ли равенство 
|
| 12) | Верно ли равенство 
|
| 13) | Обязательно ли существуют произведения  , если , если  ? ?
|
| 14) | Может ли произведение матриц быть числом? |
| 15) | Как изменятся произведения матриц  и и  , если переставить , если переставить  -ю и -ю и  -ю строки матрицы -ю строки матрицы  ? ?
|
| 16) | Как изменится произведение матриц  и и  , если к , если к  -й строке матрицы А прибавить -й строке матрицы А прибавить  -ю строку, умноженную на число -ю строку, умноженную на число 
|
| 17) | Как изменится произведение матриц  и и  , если переставить , если переставить  -й и -й и  -й столбцы матрицы -й столбцы матрицы  ? ?
|
| 18) | Как изменится произведение матриц  и и  , если к , если к  -му столбцу матрицы В прибавить -му столбцу матрицы В прибавить  -й столбец, умноженный на число -й столбец, умноженный на число 
|
| К главе II. | |
| 19) | Могут ли все алгебраические дополнения некоторой матрицы  быть равны соответствующим минорам, т. е. быть равны соответствующим минорам, т. е.  ? ?
|
| 20) | Могут ли все алгебраические дополнения некоторой матрицы  быть равны соответствующим минорам быть равны соответствующим минорам  ? ?
|
| 21) | Могут ли все алгебраические дополнения некоторой матрицы  быть равны соответствующим
элементам быть равны соответствующим
элементам  ? ?
|
| 22) | Может ли определитель 2-го порядка принимать значение большее, чем определитель 5-го порядка? |
| 23) | Может ли определитель изменить знак на противоположный при транспонировании матрицы? |
| 24) | Дана квадратная матрица n-го порядка  . Чему равна сумма . Чему равна сумма  ? ?
|
| 25) | Можно ли вычислить миноры, дополнительные к элементам не квадратной матрицы? |
| 26) | Как изменится определитель 3-го порядка, если его строки переставить следующим образом: первую – на место второй, вторую – на место третьей, третью – на место первой? |
| 27) | Как изменится определитель n-го порядка, если его строки переставить следующим образом: первую – на место второй, вторую – на место третьей, … ,  -ю – на место -ю – на место  -й, -й,  -ю – на место первой? -ю – на место первой?
|
| 28) | Сколько всего миноров у квадратной матрицы  -го порядка? -го порядка?
|
| 29) | К главе III. |
| 30) | Могут ли различные методы решения системы линейных уравнений (метод Крамера и метод обратной матрицы) дать различные ответы? |
| 31) | Возможно ли, чтобы система линейных уравнений имела решение с помощью метода Гаусса, но не имела бы решения по формулам Крамера? |
| 32) | В системе n линейных уравнений с n неизвестными поменяли местами два уравнения. Изменятся ли формы записи решения с помощью обратной матрицы и по формулам Крамера? Изменится ли общее решение? |
| 33) | Доказать, что формулы Крамера являются другой формой записи решения  системы линейных уравнений системы линейных уравнений 
|
| 34) | Решить систему линейных уравнений:

|
|
из
5.00
|
Обсуждение в статье: К разделу: «Элементы линейной алгебры анализа» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |
Популярное:
Почему двоичная система счисления так распространена?: Каждая цифра должна быть как-то представлена на физическом носителе...
Как распознать напряжение: Говоря о мышечном напряжении, мы в первую очередь имеем в виду мускулы, прикрепленные к костям ...
Личность ребенка как объект и субъект в образовательной технологии: В настоящее время в России идет становление новой системы образования, ориентированного на вхождение...
Почему человек чувствует себя несчастным?: Для начала определим, что такое несчастье. Несчастьем мы будем считать психологическое состояние...

©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (878)
Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

