 |
Главная |
Тема 4.3. Численное решение обыкновенных дифференциальных уравнений
|
из
5.00
|
Построение интегральной кривой. Метод Эйлера.
Практическое занятие
Примерный перечень практических занятий
Тема 1.1. Вычисление пределов с использованием первого и второго замечательного пределов. Исследование функции на непрерывность. Нахождение по алгоритму производных. Вычисление производной сложных функций. Интегрирование простейших определенных интегралов. Решение прикладных задач. Нахождение частных производных.
Тема 1.2. Решение дифференциальных уравнений с разделяющимися переменными; однородных дифференциальных уравнений первого порядка.
Линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. Решение прикладных задач.
Тема 1.3. Решение простейших дифференциальных уравнений линейных относительно частных производных.
Тема 3.1. Решение простейших задач на определение вероятности с использованием теоремы сложения вероятностей.
Тема 4.1. Вычисление интегралов по формулам прямоугольников, трапеций и формуле Симпсона. Оценка погрешности.
Тема 4.3. Нахождение значения функции с использованием метода Эйлера.
Контрольные задания
Вариант 1
1. Понятие предела функции. Теоремы о пределах функций.
2. Вычислите:
а) 
б) 
в) 
3. Общая схема исследования функций и построения графиков.
4. Найти производную
а) y = ln (sin x ·  )
)
б) y = 
в) y = tg4 (x2 – 3x)
г) y = 2 
5. Исследовать функцию и построить ее график
а) f(x) = 12 x – x3 б) f(x) = x4 – 2x3 + 6x – 4
6. Вычислить:
а) ∫ (x2 + 3x2 + x + 1) dx
б) ∫ (2x + 3x) dx
0
в) ∫ (  ) dx
) dx
1
7. Задачи, приводящие к дифференциальным уравнениям.
8. Элементы и множества. Задания множеств. Операции над множествами.
9. Численное интегрирование. Способы представления функции в виде прямоугольников и трапеций.
Вариант 2
1. Что называется приращением аргумента х и приращением функции f(x) в точке xo ? Раскройте геометрический смысл этих приращений и сформулируйте соответствующее определение непрерывности функции.
2. Вычислите:
а) 
б) 
в) 
3. Наибольшее и наименьшее значения функции на отрезке.
4. Найти производную
 |
а) y = √2x – sin 2x
б) y = e 
в) y = 1/3 x3 · cos x/3
г) y = 3x · log2 (x-1)
5. Исследовать функцию и построить ее график
а) f(x) = x3/3 + x2 б) f(x) = x3 – 6x2 + 2x – 6
6. Вычислить:
а) ∫ (x4 +  +3
+3  +1/х2+1/х) dx
+1/х2+1/х) dx
б)  (2/1 + x2 – 3/
(2/1 + x2 – 3/  ) dx
) dx
в)  x(3 – x) dx
x(3 – x) dx
7. Дифференциальные уравнения с разделяющими переменными.
8. Свойства операций над множествами отношения. Свойства отношений.
9. Численное интегрирование. Формулы прямоугольников. Формула трапеций.
Вариант 3
1. Непрерывность элементарных функций. Свойства функций, непрерывных на отрезке.
2. Вычислите:
а) 

б)  (4 x2 – 2x + 1)
(4 x2 – 2x + 1)
в) 
3. Понятие дифференциала функции. Геометрический смысл дифференциала.
4. Найти производную
а) y =  + 5/х2 – 3/х3 + 2
+ 5/х2 – 3/х3 + 2
б) y =  · ln x
· ln x
в) y =  · arcctg x
· arcctg x
г) y = 
5. Исследовать функцию и построить ее график
а) f(x) = x3/3 - x2 – 3x б) f(x) = 6x - x3
6. Вычислить:
а) ∫ (sin x + 5 cos x) dx
б) ∫ 2 dx / sin2 x/2
 1
1
в) ∫ dx / √4-x2
0
7. Однородные дифференциальные уравнения первого порядка.
8. Графы. Основные определения. Элементы графов. Виды графов и операции над ними.
9. Численное интегрирование. Формула Симпсона.
Вариант 4
1. Производная функции, ее геометрический и механический смысл.
2. Вычислите:
x 2 + 6x + 8
 а)
а) 
x2 + 8
9 – х2
 б)
б) 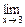
√3x - 3
(x + h)3 – x3
 в)
в) 
h
3. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла.
4. Найти производную
 |
а) y = b/a · √a2 - x2
б) y = ¼ cos4 4x

в) y = arcsin · √1-2x
г) y = еcos x + (x-3)4
5. Исследовать функцию и построить ее график
а) f(x) = x3 + 6x2 + 9x б) f(x) = x3 - x
6. Вычислить:
а) ∫ cos x/2 dx в) 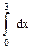 /
/ 
б) ∫ (  – 2x) dx
– 2x) dx
7 Линейные однородные уравнения второго порядка с постоянными коэффициентами.
8 Понятие события и вероятности события. Достоверные и невозможные события..
9 Абсолютная погрешность при численном интегрировании.
Вариант 5
1. Уравнения касательной и нормали к кривой. Производная сложной функции.
2. Вычислите:
а)  (x3 + 5x2 + 6x + 1)
(x3 + 5x2 + 6x + 1)
х2 - 25
 б)
б) 
x - 5
в) 
3. Возрастание и убывание функций. Какие точки называются критическими?
4. Найти производную
 |
а) y = ln √ 2x - 1
б) y = sin5 (1-3x2) 4
x
 в) y =
в) y =
 √a2 + x2
√a2 + x2
г) y = 
5. Исследовать функцию и построить ее график
а) f(x) = x4/ 4 + x2 б) f(x) = x4 – 8 x3 + 24 x2
6. Вычислить:
а) ∫ dx/ 2 cos2 x/4
б) ∫ (2x – sin 3x) dx
в) ∫ (x2 + 1/x4) dx
1
7. Простейшие дифференциальные уравнения в частных производных.
8. Классическое определение вероятностей. Теорема сложения вероятностей.
9. Численное дифференцирование. Интерполяционные формулы Ньютона.
Вариант 6
1. Вычисления производных. Правила и формулы дифференцирования. Физический смысл производной.
2. Вычислите:
x3 + 4x - 1
 а)
а) 
3x2 + x + 2
х2 – 5x + 6
 б)
б) 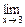
x - 3
x2
 в)
в) 
 √ x2 + 1 - 1
√ x2 + 1 - 1
3. Дайте определение неопределенного интеграла. Таблица основных интегралов (доказать).
4. Найти производную
 |
а) y = (x + 1)2 · √ x - 1

б) y = arcctg √x2 + 2x

в) y = lg √x2+ 4
г) y = е sin 2x · 2x
5. Исследовать функцию и построить ее график
а) f(x) = x4/ 4 - x3 /3 б) f(x) = x4 – 8 x2 - 9
6. Вычислить:
а) ∫ (x4 – cos 2x) dx
б) ∫ (е2x + sin x/4) dx
в) ∫ dx/ x · 
1
7. Дифференциальные уравнения линейные относительно частных производных.
8. Классическое определение вероятностей. Теорема умножения вероятностей.
9. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона.
Вариант 7
1. Понятие о производных высших порядков. Механический смысл второй производной.
2. Вычислите:
х2 - x - 2
 а)
а) 
x3 + 1
х2 + 3x + 2
 б)
б) 
x2 – x - 6
в) 
3. Дайте определение первообразной для функции f(x) на промежутке. Приведите примеры функций, имеющих первообразные. В чем состоит смысл действия интегрирования.
4. Найти производную
а) y = arcsin 
 б) y =
б) y =
(x3 – 1)4
в) y = 
г) y = 
5. Исследовать функцию и построить ее график
а) f(x) = x4/ 4 - 2x2 б) f(x) = x3 – 4 x2 – 3x + 6
6. Вычислить:
а) ∫ (x4 – 2/x3 + x6/6) dx
б) ∫ (sin 3x + cos x/4) dx
в) ∫ (2x2 – 3x – ½  ) dx
) dx
1
7. Числовые ряды. Сходимость и расходимость числовых рядов.
8. Способы задания случайной величины. Определения непрерывной и дискретной случайных величин.
Вариант 8
1. Понятие производной функции в точке. Признаки возрастания и убывания функции.
2. Вычислите:
x4 - 2x2 - 3
 а)
а) 
x2 - 3x + 2
х2 + 6x + 8
 б)
б) 
x3 + 8
в) 

3. Основные методы интегрирования. Понятие определенного интеграла. Основные свойства определенного интеграла.
4. Найти производную
arccos x
 а) y =
а) y =
x
3x2 – 2x - 4
 б) y =
б) y =
2x - 1
в) y = cos4 (x2 – x + 1)3
г) y = 4x · sin 2 x/3
5. Исследовать функцию и построить ее график
а) f(x) = 3x5 - 5x3 б) f(x) = 3 + 2x2 – 8 x3
6. Вычислить:
а) ∫ (1 – 3 cos x/4) dx

б) ∫ √ 1-x dx
1
в) ∫ (1 -  ) dx
) dx
-1
7. Признак сходимости Даламбера. Знакопеременные ряды
8. Случайная величина. Закон распределения случайной величины.
9. Численное решение обыкновенных дифференциальных уравнений.
Вариант 9
1. Понятие экстремума функции. Необходимые условия существования экстремума. Достаточные условия существования экстремума.
2. Вычислите:
а) 
б) 
в) 
3. Понятие определенного интеграла. Формула Ньютона-Лейбница. Таблица основных интегралов (докажите одну из них).
4. Найти производную
а) f(x) = x-2 · 
б) y = 
в) y = x · arcsin x + 
г) y = 4cos x/4 · sin 3 x
5. Исследовать функцию и построить ее график
а) f(x) = x5 /5 - x4 + x3 б) f(x) = 1/3 x3 – 1/2 x2 – 2x + 1
6. Вычислить:
а) ∫ (x/2 - sin2x/2) dx
б) ∫ (sin 3x – ½ x4) dx
8
в) ∫ (4x – 1/ 3  ) dx
) dx
1
7. Абсолютная и условная сходимость рядов. Функциональные ряды.
8. определение математического ожидания, дисперсии дискретной случайной величины.
9. Построение интегральной кривой. Метод Эйлера.
Вариант 10
1. Выпуклость графика функции. Точки перегиба. Асимптоты кривой.
2. Вычислите:
√1 + x - 1
 а)
а) 
x
б) 
tg 4x
 в)
в) 
x
3. Площадь криволинейной трапеции. Геометрический смысл определенного интеграла.
4. Найти производную
а) y = x ·  + x2 /
+ x2 /  - 2
- 2 
б) y = arctg 
в) y = (x3 – 1) (x2 + x + 1)
г) y = 5x · ln sin x/3
5. Исследовать функцию и построить ее график
а) f(x) = x3 - 6x2 + x б) f(x) = 2 – 3x + x3
6. Вычислить:
а) ∫ (x4 + 2/x3 – sin3x) dx
б) ∫ (cos 4x – e3x) dx
3
в) ∫ (sin x + 2/cos2 x) dx
0
7. Степенные ряды. Разложение элементарных функций в ряд Маклорена.
8. Математическое определение дискретной случайной величины. Дисперсия случайной величины.
9. Нахождение значения функции с использованием метода Эйлера.
Методические указания
Раздел 1. Математический анализ.
Тема 1.1. Дифференциальное и интегральное исчисление.
Определение: пусть f(x) - функция определена в некоторой проколотой окрестности точки а. Если она непрерывна в точке а, то назовем ее значение в точке а пределом при стремлении х к а и будем писать lim f(x) = f(a). Если функция разрывна в точке а, то может случится, что этот разрыв устранимый. Тогда можно изменить значение функции в точке а или доопределить ее в этой точке так, что в результате получится функция y= f(x), непрерывная в точке а:
 f(x), если x ≠ a
f(x), если x ≠ a
F(x) =
b, если х = а
Число b = f(а) называется пределом функции у = f(x) при х→ а. В этом случае пишут
 f(x) = b.
f(x) = b.
Пример.
Вычислите:
х2 - 5х + 1
 lim непрерывна в точке х = 1, то предел функции при х→ 1 равен
lim непрерывна в точке х = 1, то предел функции при х→ 1 равен
x → 1 3 х + 5
ее значению в этой точке, т.е.
х2 - 5х + 1 1 – 5 + 1 3


 lim = = -
lim = = -
x → 1 3 х + 5 3 + 5 8
|
из
5.00
|
Обсуждение в статье: Тема 4.3. Численное решение обыкновенных дифференциальных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

