ЛЕКЦИЯ 16. Преобразование Фурье

Будем рассматривать непериодическую функцию как предельный случай периодической при неограниченно возрастающем периоде:

Перейдем к пределу при L → ∞. Вместо 1/L введем основную круговую частоту _. Эта величина есть частотный интервал между соседними гармониками, частота которых равна 2πk/L. При предельном переходе сделаем замену по следующей схеме:

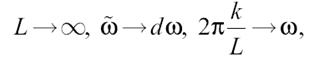
где ω — текущая частота, изменяющаяся непрерывно, dω — ее приращение. Сумма перейдет в интеграл и мы получим

Эти формулы являются основными в теории спектров сигналов. Они представляют собой пару преобразований Фурье, связывающих между собой вещественную функцию времени f(x) и комплексную функцию частоты F(ω). Для обозначения этой связи будем использовать в дальнейшем символическую запись:

При этом функция f(x) описывается суммой бесконечно большого числа бесконечно малых колебаний бесконечно близких частот. Комплексная амплитуда каждого такого колебания составляет величину

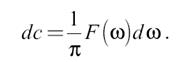
Частотный интервал между двумя соседними колебаниями бесконечно мал и равен dω. Величина

выражает не непосредственно спектр, а так называемую спектральную плотность, то есть распределение сигнала по спектру. Однако эту деталь обычно опускают и называют F(ω) комплексным спектром непериодического сигнала, а абсолютное значение (модуль) этой величины называют просто спектром.

Рассмотрим некоторые свойства спектров, основанные на свойствах преобразования Фурье.

ЛЕКЦИЯ 17. Спектры импульсов 1

Рисунок 17.1 – Прямоугольный импульс и его спектр

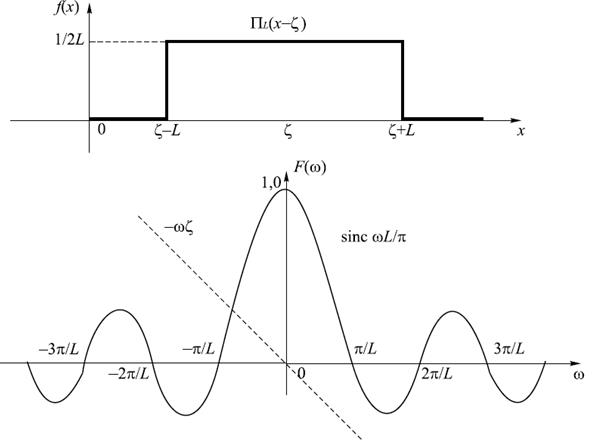
Рисунок 17.2 – Сдвинутый прямоугольный импульс и его спектр

В соответствии с формулами получим

Рисунок 17.3 – Функция отсчетов и ее спектр

ЛЕКЦИЯ 18. Спектры импульсов 2

Графики меандра и его спектра приведены на рисунке 18.1.

Треугольный импульс (рисунок 18.2) можно записать в виде формулы

Рисунок 18.1 – Два прямоугольных импульса разной полярности и спектр их сумм

Экспоненциальный спад описывается функцией, отличной от нуля, только при x ≥ 0:

Рисунок 18.2 – Треугольный импульс и его спектр

График амплитуды и фазы экспоненциального импульса приведен на рисунке 18.3.

Рисунок 18.3 – Спектр экспоненциального импульса

то есть также описывается гауссовой функцией, в чем и состоит двойственность рассматриваемого сигнала. Функция Гаусса представлена на рисунке 18.4а, а спектр функции – на рисунке 18.4б.

Рисунок 18.4 – Гауссов импульс (а) и его спектр (б)