Методика выполнения работы. 1. Алгоритм в виде блок-схемы:

1. Алгоритм в виде блок-схемы:

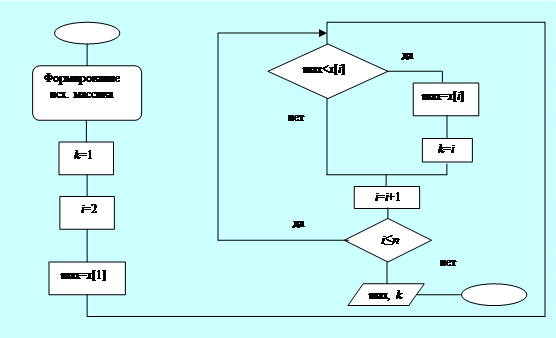
Рис. 5.7. Блок-схема алгоритма поиска максимального элемента одномерного массива и его номера в массиве

 

2. Программа на основе алгоритма рис.5.7:

 

Program Maximum;

Uses crt;

Const n=25;

Var i,k,max:Integer;

x:Array[1..n] Of Integer;{Объявление одномерного массива}

Begin

Clrscr;

Randomize;{Формирование новых данных при очередном запуске программы}

Writeln(‘Исходный массив’);

For i:=1 To n Do{Начало циклического алгоритма арифметического типа}

Begin x[i]:=Random(100);{Обращение к датчику случайных чисел}

Write(x[i]:4)

End;{Конец циклического алгоритма арифметического типа}

Writeln;

k:=1;

max:=x[1];

For i:=2 To n Do

If max<x[i] Then

Begin max:=x[i];k:=i End;

Writeln(‘Максимальный элемент’,max:4,’ Его номер в массиве’,k:4)

End.

3. Наберите, откомпилируйте и исправьте возможные ошибки. Затем запустите программу на счет.

4. Убедитесь в правильности работы программы. В противном случае внесите коррективы в алгоритм.

5. Внесите изменения в программу так, чтобы она искала минимальный элемент.

 

Задание № 2. Построить алгоритм для вычисления корня уравнения с точностью ε=10^-4 методом простой итерации. Принять за начальное значение корня x₀=2. Вывести на экран корень уравнения до 5-го знака и число итераций. Разработать, набрать и отладить программу, реализующую этот алгоритм.

Методика выполнения работы

1. Алгоритм в виде блок-схемы:

 

Рис. 5.8. Блок-схема алгоритма нахождения корней методом простой итерации

 

 

2. Программа на основе алгоритма рис.5.8:

 

Program Root;

Uses crt;

Var x0,x,eps:Real;

n:Integer;

Begin

Clrscr;

eps:=1E-4;

x0:=2;

x:=exp(ln(29+3*x0*x0+8*x0)*(1/4));

n:=1;

While abs(x0-x)>eps Do{Начало итерационного цикла с предусловием}

Begin

x0:=x;

x:=exp(ln(29+3*x0*x0+8*x0)*(1/4));

n:=n+1

End;{Конец итерационного цикла с предусловием}

Writeln(‘Корень=’,x:10:5,’ Количество итераций=’,n)

End.

3. Наберите, откомпилируйте и исправьте возможные ошибки. Затем запустите программу на счет. Должен быть получен следующий результат: Корень равен 2.98770. Количество итераций равно 8.

4. Изменяя начальное приближение x₀, выясните, как влияет начальное приближение на количество итераций.

5. Измените программу так, чтобы итерационный цикл осуществлялся с постусловием – вместо оператора While использовать оператор Repeat. Результат работы программы не должен измениться.

 

Задания для самостоятельной работы

Разработать алгоритм в виде блок-схемы, составить программу на языке Паскаль.

 

Вариант 1.1

где x принимает значения в интервале [-1÷3] с шагом 0.2.

 

Вариант 1.2

где x принимает значения в интервале [0÷10] с шагом 0.5. Значение b вводится с клавиатуры.

 

Вариант 1.3

Даны два одномерных массива: A и B. Элементы массивов – вещественные числа. Найти минимальное число среди 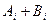, где i изменяется от 1 до 15.

 

Вариант 1.4

 

Дан одномерный массив X. Элементы массива – числа целого типа. Размер массива – 20. Найти S – сумму элементов массива, не превышающих 2.

 

Вариант1. 5

 

Дан одномерный массив С. Элементы массива – числа вещественного типа. Размер массива – 10. Найти P – произведение элементов массива, отличных от нуля.

 

 

Вариант 2.1

Методом простой итерации определить корень уравнения

с точностью ε =10^-3, если x₀ = 10. Для организации итерационного цикла использовать оператор цикла с предусловием.

 

Вариант 2.2

Методом простой итерации определить корень уравнения

с точностью ε =10^-4, если x₀ = 1.1. Для организации итерационного цикла использовать оператор цикла с постусловием.

 

 

Вариант 2.3

Для уравнения получена итерационная формула

Определить методом простой итерации значение корня с точностью ε =10^-3, если x₀ = 1.5.

Для организации итерационного цикла использовать оператор цикла с предусловием.

 

Вариант 2.4

Найти сумму ряда

с заданной точностью ε =10^-3.

Вариант 2.5

 

Найти сумму ряда

при x = 0.1 с заданной точностью ε =0.5∙10^-4.