Уравнение неразрывности потока

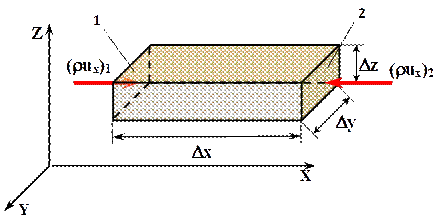
Уравнение неразрывности потока представляет собой закон сохранения массы для элементарного объема пористой среды. Выделим мысленно в пористой среде, в которой происходит движение однородной сжимаемой жидкости или газа, объем в виде параллелепипеда с ребрами Dx, Dy, Dz (рисунок 1.5). Найдем массу, которая входит в выделенный объем вдоль оси x за время Dt. Обозначим левую и правую грани индексами 1 и 2. Через левую грань войдет масса (r u_x)₁ Dy Dz Dt, а через правую грань войдет масса (r u_x)₂ Dy Dz Dt.

Рисунок 1.5 – Схема элемента пласта

Тогда внутри объема останется масса равная разности этих масс d m_x. Если расстояние между гранями Δx устремить к нулю, то эта разность преобразуется к виду:

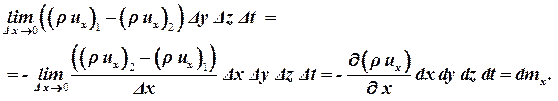
(1.33)

Аналогично можно найти массы, которые останутся внутри объема при движении вдоль осей y и z. Таким образом, общая масса, оставшаяся внутри объема, равна сумме этих масс:

.

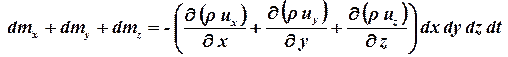(1.34)

С другой стороны, масса жидкости внутри порового пространства выделенного объема равна произведению плотности r, пористости m и объема. Поэтому увеличение массы для бесконечно малого промежутка времени равно:

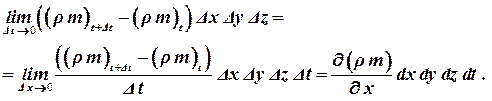
(1.35)

Прировняв эти массы и преобразовав полученное уравнение, получим дифференциальное уравнение неразрывности потока:

.

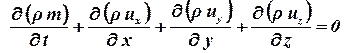(1.36)

Первое слагаемое в этом уравнении отвечает за нестационарность движения, поэтому если оно равно нулю, по движение стационарно. Остальные слагаемые отвечают за движение вдоль соответствующих осей.

Отметим, что уравнение неразрывности потока справедливо только в том случае, если поток неразрывен, то есть в потоке нет других жидкостей или газов, а также нет источников или стоков, выделяющих или поглощающих флюид (химических реакций, фазовых превращений и т. д.).

В дивергентном виде это уравнение записывается:

.

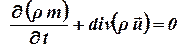(1.37)

В частных случаях уравнение упрощается.

Для плоскопараллельного потока (приток к галерее) оно имеет вид:

.

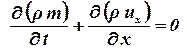(1.38)

Для плоскорадиального потока (приток к скважине):

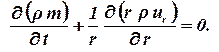
(1.39)

Для радиально–сферического потока:

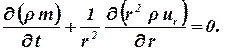
(1.40)

При стационарном движении уравнение неразрывности удобно записать в интегральном виде. Для этого выберем элементарную струйку или поток, боковые поверхности которого непроницаемы для жидкости, а торцевые представляют собой поперечные сечения, то есть перпендикулярны направлению скорости. Проинтегрируем уравнение неразрывности потока по объему между этими сечениями и применим теорему Остроградского – Гаусса, то есть перейдем от интеграла по объему к интегралу по боковой поверхности этого объема:

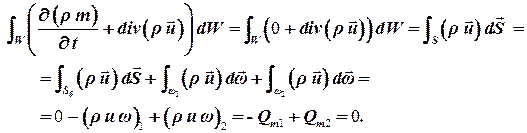
(1.41)

В этом выражении производная по времени обратилась в ноль, так как движение стационарное. Интеграл по боковой поверхности равен нулю, так как скалярное произведение вектора скорости и нормали к боковой поверхности S_Б равно нулю (угол между этими векторами составляет 90° из–за того, что граница непроницаема). В первом поперечном сечении угол между вектором скорости и нормали к поперечному сечению составляет 180°, поэтому косинус этого угла в скалярном произведении равен минус единице. Поэтому интеграл по поверхности первого поперечного сечения представляет собой массовый расход в этом поперечном сечении с отрицательным знаком.

Аналогично интеграл по поверхности второго поперечного сечения представляет собой массовый расход в этом сечении, но с положительным знаком, так как угол между вектором скорости и нормали к поперечному сечению равен нулю.

Из полученного выражения следует, что массовый расход в любом поперечном сечении потока при стационарном движении – величина постоянная:

.

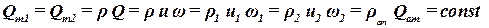(1.42)

Если происходит движение несжимаемой жидкости, то плотность в разных сечениях будет постоянной. Поэтому для несжимаемой жидкости будет постоянным не только массовый расход, но и объемный расход:

.

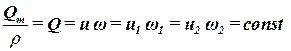(1.43)