Закон парности касательных напряжений

Рассмотрим равновесие малого выделенного элемента из твердого деформируемого тела, показанного на рис.4.1. Запишем уравнения равновесия для пространственной системы сил в виде:

ΣМ_z=0: ,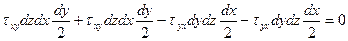

ΣМ_х=0: ,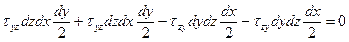

ΣМ_у=0: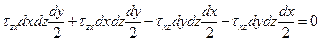

откуда получаем:

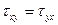
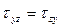(4.2)

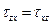
Таким образом, касательные напряжения τ на паре взаимно перпендикулярных площадок равны по величине и направлены к общему ребру или от него. В этом состоит суть закона взаимности или парности касательных напряжений, выражающийся формулами (4.2).

 

Напряжения на наклонных площадках при объёмном и при плоском напряженных состояниях

 

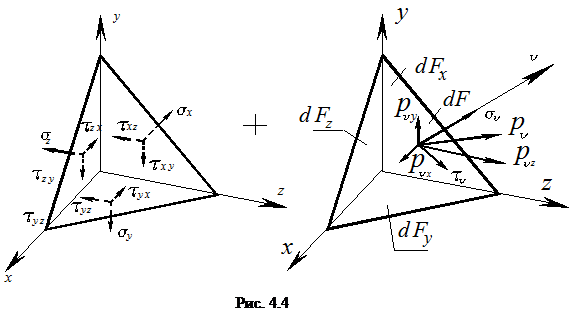
Отсечем от элементарного объёма некоторую его часть произвольной наклонной плоскостью. Положение этой плоскости зададим вектором единичной нормали ν (рис.4.4), с направляющими косинусами:

l=cos(x,ˆν)= 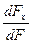, m=cos(y,ˆν)= 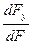, n=cos(z,ˆν)=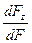

Рассмотрим равновесие полученной элементарной пирамиды. Запишем уравнения равновесия в виде суммы проекций всех сил на координатные оси. Так Σx=0, Σy=0, Σz=0 дают следующую систему уравнений:

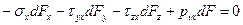
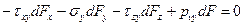
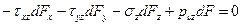
С учетом значений направляющих косинусов l, m, n получим значения составляющих полного напряжения р_ν на наклоной площадке с нормалью ν:

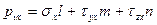
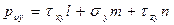(4.3)

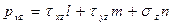
Если наклонная площадка принадлежит поверхности тела, то формулы (4.3) по существу связывают поверхностные нагрузки с компонентами тензора напряжений.

Полное напряжение на наклоной площадке, таким образом, можно определить через его составляющие:

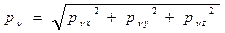(4.4)

Проектируя составляющие полного напряжения р_ν (4.3) на нормаль ν, получим с учетом значений направляющих косинусов и закона парности касательных напряжений (4.2) формулу для определения нормальных напряжений на произвольной наклонной площадке при объемном напряженном состоянии:

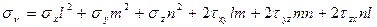(4.5)

Теперь можно определить и касательные напряжения на наклонной площадке:

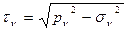
Рассмотрим частный случай плоского напряженного состояния, когда 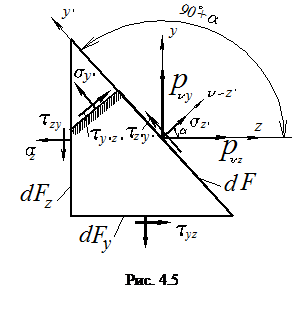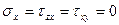, изображенный на рис.4.5. В этом случае формулы (4.3) примут более простой вид:

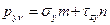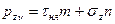, (4.6)

Направляющие косинусы: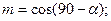

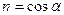
Нормальные напряжения на наклонной площадке с нормалью ν будут равны:

(*)

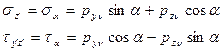C учетом зависимостей (4.6) формулы (*) можно представить в окончательном виде:

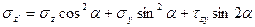(4.7)

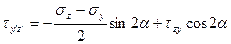(4.8)

На заштрихованной площадке, для которой β=90+α, значения нормальных и касательных напряжений будут определяться по формулам:

σ_y' = σ_zsin²α+σ_ycos²α-τ_zysin2α (4.9)

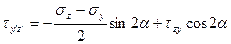(4.10)

 

Cкладывая формулы (4.7) и (4.9) получаем:

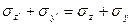(4.11)

Формула (4.11) выражает мысль о том, что сумма нормальных напряжений на паре взаимно перпендикулярных площадок есть величина постоянная, а формулы (4.8) и (4.10) ещё раз подтверждают закон парности касательных напряжений.