 |
Главная |
Условие прочности вала при кручении
|
из
5.00
|
В предыдущем параграфе мы увидели, что наибольшие касательные напряжения действуют в точках на наружной поверхности вала, где ρ = ρmax = d/2 для вала сплошного поперечного сечения и ρ = ρmax = D/2 для вала с поперечным сечением в форме кольца. Перепишем формулу (7.4) так:
 ,
,
или
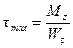 (7.7)
(7.7)
Формула (7.7) позволяет вычислять только максимальные касательные напряжения. В этой формуле Wρ – полярный момент сопротивления поперечного сечения вала кручению. Для сплошного и кольцевого сечений имеем:

 (7.8)
(7.8)
Теперь можно составить условие прочности материала в таком виде:
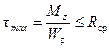 , (7.9)
, (7.9)
где Rср – расчетное сопротивление материала вала на срез;
Условие прочности (7.9) позволяет решать три типа задач.
1. непосредственно по формуле (7.9) выполнять поверочный расчет;
2. находить грузоподъёмность вала;
3. определять диаметр вала:
а) сплошной вал:
подставим первую формулу (7.8) в (7.9) получаем:


из последнего выражения следует, что диаметр
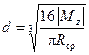 (7.10)
(7.10)
б) вал кольцевого сечения:
после подстановки второй формулы (7.8) в (7.9) получим аналогично:
 (7.11)
(7.11)
Закон Гука при кручении
Возвратимся к промежуточной формуле (7.3). С учетом, того, что  , запишем
, запишем
 (7.12)
(7.12)
Из формулы (7.12) вытекает:
 (7.13)
(7.13)
При наличии нескольких участков вала:
 (7.14)
(7.14)
Формулы (7.13, 7.14) представляют закон Гука при кручении. Интегрирование в них выполняется по длине каждого участка li вала. В случае если Мz = const и GJρ = const, формула (7.14) заменяется такой суммой:
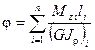 (7.15)
(7.15)
Таким образом, формула (7.15) позволяет определять абсолютные углы закручивания валов ступенчато переменной жесткости в пределах упругости.
Условие жесткости вала
Жесткость оценивается по относительному углу закручивания каждого участка вала, т.е.
 , (7.16)
, (7.16)
где [θ] - допустимая сколь угодно малая величина относительного угла закручивания. С учетом формул (7.5) и (7.6) диаметры сплошного и кольцевого сечений по условию жесткости (7.16) можно определить так:
 ;
; 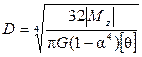 . (7.17)
. (7.17)
Потенциальная энергия упругой деформации при кручении
 При определении потенциальной энергии деформации при кручении вала будем предполагать работу его материала в рамках закона Гука. В этом случае существует пропорциональная зависимость между абсолютным углом закручивания φ и крутящим моментом Мz. Диаграмма кручения показана для этого случая на рис. 7.8.
При определении потенциальной энергии деформации при кручении вала будем предполагать работу его материала в рамках закона Гука. В этом случае существует пропорциональная зависимость между абсолютным углом закручивания φ и крутящим моментом Мz. Диаграмма кручения показана для этого случая на рис. 7.8.
Работа внешних сил А затраченная на закручивание, равна потенциальной энергии U, накопленной в стержне.
А = U
Работа А численно равна заштрихованной площади диаграммы кручения.
А=U=½Мzφ (7.18)
Подставляя вместо Мz или вместо угла закручивания φ в соответствии с формулой (7.15), получим
 (7.19)
(7.19)
В случае вала ступенчато переменной жесткости формула потенциальной энергии будет иметь вид:
 , (7.20)
, (7.20)
где i - номер ступени вала.
|
из
5.00
|
Обсуждение в статье: Условие прочности вала при кручении |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

