 |
Главная |
Построение эпюр изгибающих моментов и поперечных сил в балках
|
из
5.00
|
Для оценки прочности и жесткости изгибаемых элементов необходимо знать изменение изгибающего момента и поперечной силы по длине балки, а также их экстремальное значение. С этой целью строят эпюры изгибающих моментов и поперечных сил.
Эпюры изгибающих моментов и поперечных сил - представляют собой график, изображающий аналитическую зависимость Mx и Qy по длине балки. Ординаты на эпюрах откладываются в масштабе или соразмерно их численным значениям.
Для определения Mx и Qy в пределах каждого участка балки пользуются методом сечений.
Границами участков на балке являются точки приложения сосредоточенных сил и моментов, точки начала и конца действия распределенной нагрузки.
В пределах каждого участка проводим нормальное к оси балки сечение и рассматриваем в равновесии целиком правую или левую часть балки. Действие отброшенной части балки заменяем внутренними силовыми факторами, которые прикладываются в положительном направлении. Для рассматриваемой части составляем уравнения равновесия статики и находим Mx и Qy, которые при этом считаются внешними силовыми факторами. На основании полученных аналитических зависимостей определяем значение Mx и Qy в граничных и промежуточных точках, а затем строим эпюры.
На эпюре Qy положительная ордината откладывается вверх, а на эпюре Mx вниз. Это связано с принятым правилом знаков. Принято говорить, что эпюра Mx строится со стороны растянутого волокна балки.
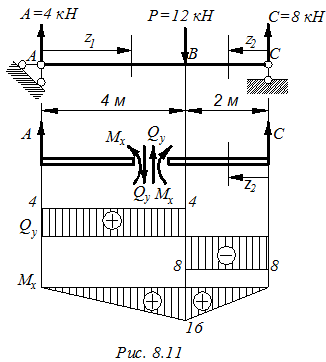 Пример 8.2.
Пример 8.2.
Построить эпюры изгибающих моментов и поперечных сил для балки, нагруженной, как показано на рис. 8.11.
1. Определяем реакции в балке: Ra=4кН, Rc = 8 кН.
2. Балка имеет два участка АВ и ВС.
3. Участок АВ. На расстоянии z1 от точки А проводим сечение 1:1 и рассматриваем в равновесии левую часть балки. Сечение может быть проведено в любом месте между точками А и В. Следовательно,
0 ≤ z1 ≥ 4
ΣFy = 0 A – Qy = 0 → Qy = A = 4 кН
Пользуясь принятым правилом знаков, для поперечной силы можно записать
Qy = A = 4 кН
Сила А приложена слева от сечения и направлена вверх.
ΣMx = 0 Az – Mx = 0 → Mx = Az
В дальнейшем будем рассуждать так: момент в рассматриваемом сечении из условия равновесия левой части равен
Mx = Az.
Находим значения изгибающего момента в граничных точках участка:
M0 = 0, M4 = 4·4 = 16 кНм
Участок ВС. Проводим сечение 2:2 на расстоянии z2 от точки С и рассматриваем в равновесии правую часть балки.
Qy = – C = – 8кН, Mx = Cz → M0 = 0, M2 = 8·2 = 16 кНм
По найденным значениям Mx и Qy строим соответствующие эпюры.
Пример 8.3.
 Построить эпюры изгибающих моментов и поперечных сил для балки, нагруженной как показано на рис. 8.12.
Построить эпюры изгибающих моментов и поперечных сил для балки, нагруженной как показано на рис. 8.12.
1. Определяем опорные реакции балки:
ΣFz = 0 → H = 0
Σmc = 0, A·6 – q·4·4 = 0 → A = 8 кН
Σma = 0, Cc·6 – q·4·2 = 0 → C= 4 кН
ΣFy = A – q·4 + B = 8 – 12 + 4 = 0
Реакции определены верно.
В дальнейшем будем полагать, что горизонтальная реакция при вертикальной нагрузке равна нулю и соответствующее уравнение для ее нахождения можно не записывать.
2. Балка имеет два участка АВ и ВС.
3. Участок АВ: 0 ≤ z1 ≥ 4
Qy = A – q·z1 → Q0 = A = 8 кН, Q4 = 8 – 3·4 = – 4 кН
Mx = A·z1 – q·z1· 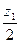 = A·z1 –
= A·z1 –  → M0 = 0, M4 = 8 кНм
→ M0 = 0, M4 = 8 кНм
 = A – q·z1 =0 → z1 =
= A – q·z1 =0 → z1 = 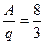 =2,66 м, М2,66 = 10,67 кН
=2,66 м, М2,66 = 10,67 кН
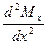 = – q кривая выпуклая
= – q кривая выпуклая
4. Участок ВС: 0 ≤ z2 ≥ 2
Qy = – С = – 4 кН
Mx = С·z2 → M0 = 0, M2 = 4·2 = 8 кНм
По найденным значениям Mx и Qy строим соответствующие эпюры.
Пример 8.4.
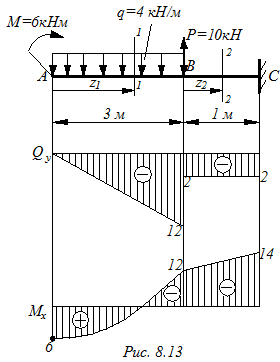 Построить эпюры изгибающих моментов и поперечных сил для консольной балки, нагруженной как показано на рис. 8.13.
Построить эпюры изгибающих моментов и поперечных сил для консольной балки, нагруженной как показано на рис. 8.13.
При построении эпюр в консольной балке реакции в заделке можно не находить. В этом случае рассматривают равновесие части балки, расположенной со стороны ее свободного конца. Балка имеет два участка АВ и ВС.
I. Участок АВ: 0 ≤ z1 ≥ 3
Qy = – q·z1 → Q0 = 0, Q3 = – 12 кН
Mx = M – q·z1· 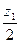 = M –
= M –  → M0 = 6 кНм,
→ M0 = 6 кНм,
М4 = – 6 кН
II. Участок ВС: 0 ≤ z2 ≥ 1
Qy = – q·3 + P = – 2 кН
Mx = M – q·3·(1,5 + z2) + P·z2 → M0 = 12 кНм,
M1 = – 14 кНм
По найденным значениям Mx и Qy строим соответствующие эпюры.
|
из
5.00
|
Обсуждение в статье: Построение эпюр изгибающих моментов и поперечных сил в балках |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

