 |
Главная |
Элементы линейной алгебры. 51 – 60. Дана система линейных уравнений
|
из
5.00
|
51 – 60. Дана система линейных уравнений
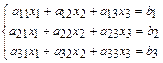
Доказать ее совместность и решитьтремя способами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления. Проверить правильность вычисления обратной матрицы, используя матричное умножение.
| 51. | 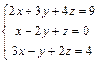
| 52. | 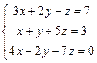
|
| 53. | 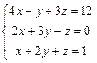
| 54. | 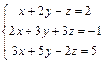
|
| 55. | 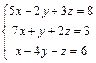
| 56. | 
|
| 57. | 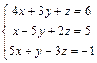
| 58. | 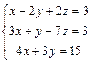
|
| 59. | 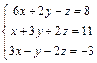
| 60. | 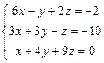
|
61 – 70. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
| 61. | 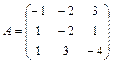
| 62. | 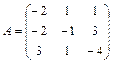
|
| 63. | 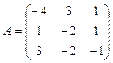
| 64. | 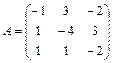
|
| 65. | 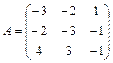
| 66. | 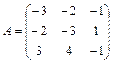
|
| 67. | 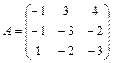
| 68. | 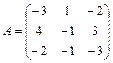
|
| 69. | 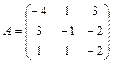
| 70. | 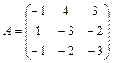
|
71 – 80. Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения w3 + z = 0.
| 71. | 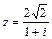
| 72. | 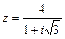
| 73. | 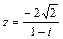
|
| 74. | 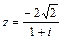
| 75. | 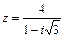
| 76. | 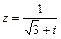
|
| 77. | 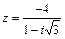
| 78. | 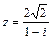
| 79. | 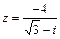
|
| 80. | 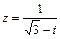
|
Введение в математический анализ
81 - 85. Построить график функции 
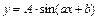 преобразованием графика функции
преобразованием графика функции 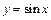 .
.
| 81. | 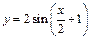
| 82. | 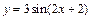
|
| 83. | 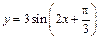
| 84. | 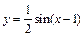
|
| 85. | 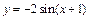
|
86 - 90. Построить график функции 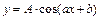 преобразованием графика функции
преобразованием графика функции 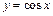 .
.
| 86. | 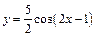
| 87. | 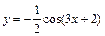
|
| 88. | 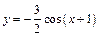
| 89. | 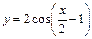
|
| 90. | 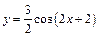
|
91 – 100. Найти пределы функций, не пользуясь правилом Лопиталя.
91. a) 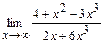 ; б)
; б) 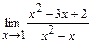 ;
;
в) 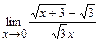 ; г)
; г) 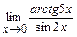 ; д)
; д) 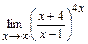 .
.
92. a) 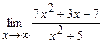 ; б)
; б) 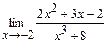 ;
;
в) 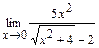 ; г)
; г) 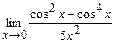 ; д)
; д) 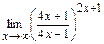 .
.
93. a) 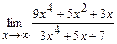 ; б)
; б) 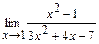 ;
;
в) 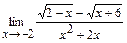 ; г)
; г) 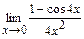 ; д).
; д). 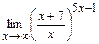
94. a) 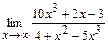 ; б)
; б) 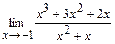 ;
;
в) 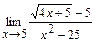 ; г)
; г) 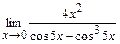 ; д)
; д) 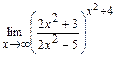 .
.
95. a) 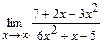 ; б)
; б) 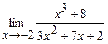 ;
;
в) 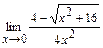 ; г)
; г) 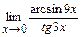 ; д)
; д) 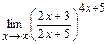 .
.
96. a) 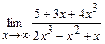 ; б)
; б) 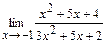 .
.
в) 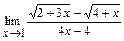 ; г)
; г) 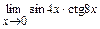 ; д)
; д) 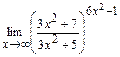 .
.
97. a) 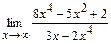 ; б)
; б) 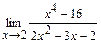 ;
;
в) 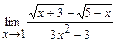 ; г)
; г) 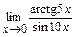 ; д)
; д) 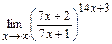 .
.
98. a) 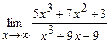 ; б)
; б) 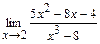 ;
;
в) 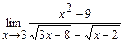 ; г)
; г) 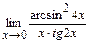 ; д)
; д) 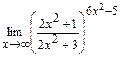 .
.
99. a) 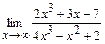 ; б)
; б) 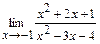 ;
;
в) 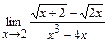 ; г)
; г) 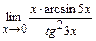 ; д)
; д) 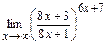 .
.
100. a) 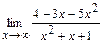 ; б)
; б) 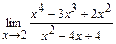 ;
;
в) 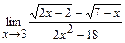 ; г)
; г) 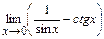 ; д)
; д) 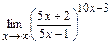 .
.
101 – 110. Задана функция y = f(x) и два значения аргумента x1 и x2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
101. 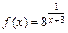 , x1 = 0, x2 = –3.
, x1 = 0, x2 = –3.
102. 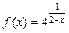 , x1 = 0, x2 = 2.
, x1 = 0, x2 = 2.
103. 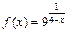 , x1 = 2, x2 = 4.
, x1 = 2, x2 = 4.
104. 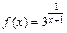 , x1 = 1, x2 = –1.
, x1 = 1, x2 = –1.
105. 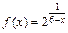 , x1 =4, x2 = 6.
, x1 =4, x2 = 6.
106. 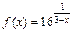 , x1 = 1, x2 = 3.
, x1 = 1, x2 = 3.
107. 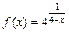 , x1 = 2, x2 = 4.
, x1 = 2, x2 = 4.
108. 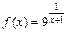 , x1 = 1, x2 = –1.
, x1 = 1, x2 = –1.
109. 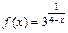 , x1 = 2, x2 = 4.
, x1 = 2, x2 = 4.
110. 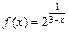 , x1 = 1, x2 = 3.
, x1 = 1, x2 = 3.
111 - 120. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
111. 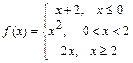 ; 112.
; 112. 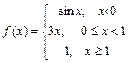 ;
;
113. 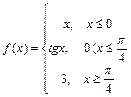 ; 114.
; 114. 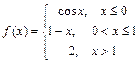 ;
;
115. 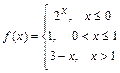 ; 116.
; 116. 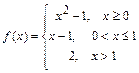 ;
;
117. 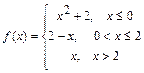 ; 118.
; 118. 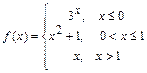 ;
;
119. 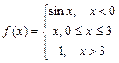 ; 120.
; 120. 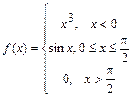 .
.
4. Производная и еЁ приложения
121 - 130. Найти производные 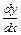 данных функций.
данных функций.
| 121. | a) 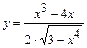 ; ;
| б) 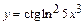 ; ;
|
в) 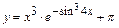 ; ;
| г) 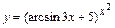 ; ;
| |
д) 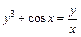 . .
| ||
| 122. | а) 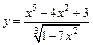 ; ;
| б) 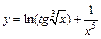 ; ;
|
в) 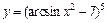 ; ;
| г) 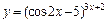 ; ;
| |
д) 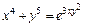 . .
| ||
| 123. | а) 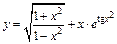 ; ;
| б) 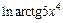 ; ;
|
в) 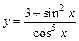 ; ;
| г) 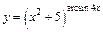 ; ;
| |
д) 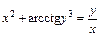 . .
| ||
| 124. | а) 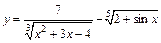 ; ;
| б) 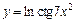 ; ;
|
в) 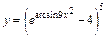 ; ;
| г) 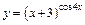 ; ;
| |
д) 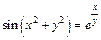 . .
| ||
| 125. | а) 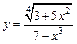 ; ;
| б) 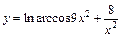 ; ;
|
в) 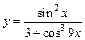 ; ;
| г) 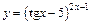 ; ;
| |
д) 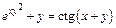 . .
| ||
| 126. | а) 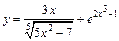 ; ;
| б) 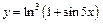 ; ;
|
в) 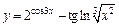 ; ;
| г) 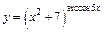 ; ;
| |
д) 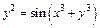 . .
| ||
| 127. | а) 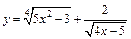 ; ;
| б) 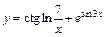 ; ;
|
в) 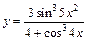 ; ;
| г) 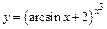 ; ;
| |
д) 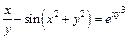 . .
| ||
| 128. | а) 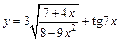 ; ;
| б) 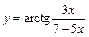 ; ;
|
в) 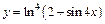 ; ;
| г) 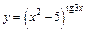 ; ;
| |
д) 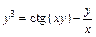 . .
| ||
| 129. | а) 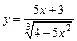 ; ;
| б) 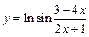 ; ;
|
в) 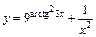 ; ;
| г) 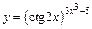 ; ;
| |
д) 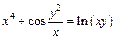 . .
| ||
| 130. | а) 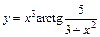 ; ;
| б) 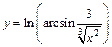 ; ;
|
в) 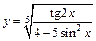 ; ;
| г) 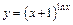 ; ;
| |
д) 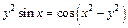 . .
|
131 - 140. Найти 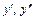 для заданных функций:
для заданных функций:
а), б) 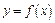 ; в)
; в) 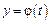 ,
, 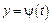 .
.
| 131. | а) 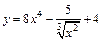 ; ;
| б) 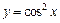 ; ;
| в) 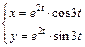
|
| 132. | а) 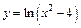 ; ;
| б) 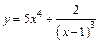
| в) 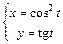 . .
|
| 133. | а) 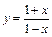 ; ;
| б) 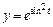 ; ;
| в) 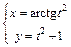 . .
|
| 134. | а) 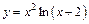 ; ;
| б) 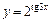 ; ;
| в) 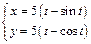 . .
|
| 135. | а) 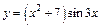 ; ;
| б) 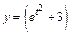 ; ;
| в) 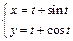 . .
|
| 136. | а) 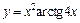 ; ;
| б) 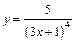 ; ;
| в) 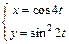 . .
|
| 137. | а) 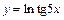 ; ;
| б) 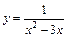 ; ;
| в) 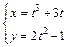 . .
|
| 138. | а) 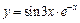 ; ;
| б) 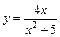 ; ;
| в) 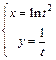 . .
|
| 139. | а) 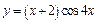 ; ;
| б) 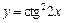 ; ;
| в) 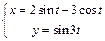 . .
|
| 140. | а) 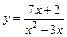 ; ;
| б) 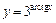 ; ;
| в) 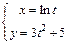 . .
|
141 – 150. Найти наибольшее и наименьшее значения функции 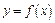 на отрезке [a;b].
на отрезке [a;b].
141. 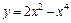 ; [0; 2]. 142.
; [0; 2]. 142. 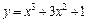 ; [–2; 1].
; [–2; 1].
143. 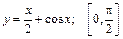 . 144.
. 144. 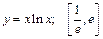 .
.
145. 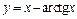 ; [–1; 1]. 146.
; [–1; 1]. 146. 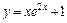 ; [–1; 0].
; [–1; 0].
147. 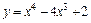 ; [–1; 1]. 148.
; [–1; 1]. 148. 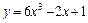 ; [0; 1].
; [0; 1].
149. 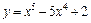 ; [–1; 2]. 150.
; [–1; 2]. 150. 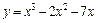 ; [–2; 0].
; [–2; 0].
5. Приложения дифференциального
Исчисления
151 – 160. Исследовать методами дифференциального исчисления функцию 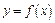 и, используя полученные результаты, построить её график.
и, используя полученные результаты, построить её график.
151. 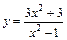 . 152.
. 152. 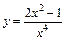 .
.
153. 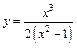 . 154.
. 154. 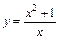 .
.
155. 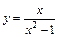 . 156.
. 156. 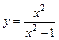 .
.
157. 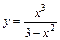 . 158.
. 158. 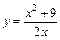 .
.
159. 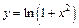 . 160.
. 160. 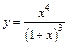 .
.
6. Дифференциальное исчисление функций
Нескольких переменных
161 – 170. Найти а) 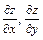 ; б)
; б) 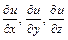 .
.
| 161. | a) 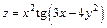 , ,
| б) 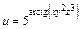 . .
|
| 162. | а) 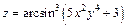 , ,
| б) 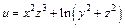 . .
|
| 163. | а) 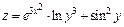 ; ;
| б) 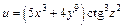 . .
|
| 164. | а) 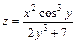 ; ;
| б) 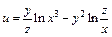 . .
|
| 165. | а) 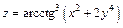 ; ;
| б) 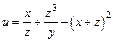 . .
|
| 166. | а) 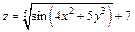 ; ;
| б) 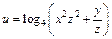 . .
|
| 167. | а) 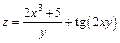 ; ;
| б) 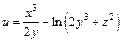 . .
|
| 168. | а) 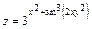 ; ;
| б) 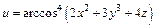 . .
|
| 169. | а) 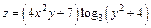 ; ;
| б) 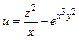 . .
|
| 170. | а) 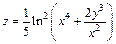 ; ;
| б) 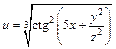 . .
|
171 – 180. Дана функция 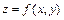 .
.
Показать, что 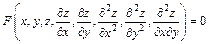 .
.
171. 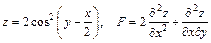 .
.
172. 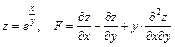 .
.
173. 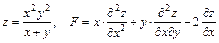 .
.
174. 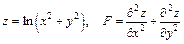 .
.
175. 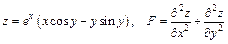 .
.
176. 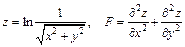 .
.
177. 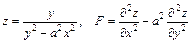 .
.
178. 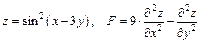 .
.
179. 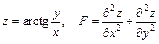 .
.
180. 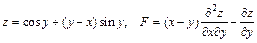 .
.
181 – 190. Найти наименьшее и наибольшее значения функции 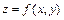 в замкнутой области D, заданной системой неравенств. Сделать чертеж.
в замкнутой области D, заданной системой неравенств. Сделать чертеж.
181. 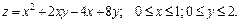 ;
;
182. 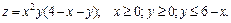
183. 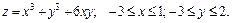
184. 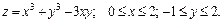
185. 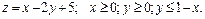
186. 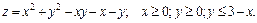
187. 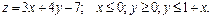
188. 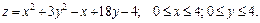
189. 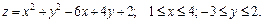
190. 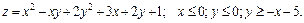
191 – 200. Даны функция 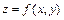 , точка
, точка 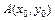 и вектор
и вектор 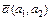 . Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора
. Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора  .
.
191. 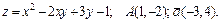
192. 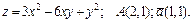
193. 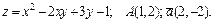
194. 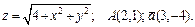
195. 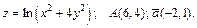
196. 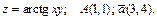
197. 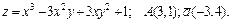
198. 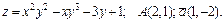
199. 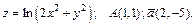
200. 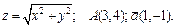
7. НеопределЁнный и определЁнный
Интегралы
201 – 210. Найти неопределенные интегралы. В пп. «а» и «б» результаты проверить дифференцированием.
| 201. | a) 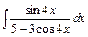 ; ;
| б) 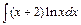 ; ;
|
в) 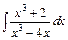 ; ;
| г) 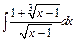 ; ;
| |
д) 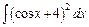 ; ;
| е) 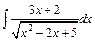 . .
| |
| 202. | a) 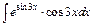 ; ;
| б) 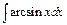 ; ;
|
в) 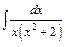 ; ;
| г) 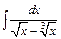 ; ;
| |
д) 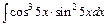 ; ;
| е) 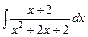 . .
| |
| 203. | a) 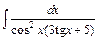 ; ;
| б) 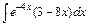 ; ;
|
в) 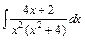 ; ;
| г) 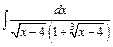 ; ;
| |
д) 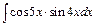 ; ;
| е) 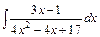 . .
| |
| 204. | a) 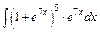 ; ;
| б) 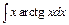 ; ;
|
в) 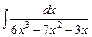 ; ;
| г) 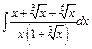 ; ;
| |
д) 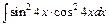 ; ;
| е) 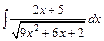 . .
| |
| 205. | a) 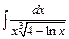 ; ;
| б) 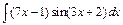 ; ;
|
в) 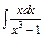 ; ;
| г) 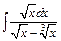 ; ;
| |
д) 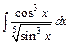 ; ;
| е) 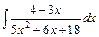 . .
| |
| 206. | a) 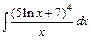 ; ;
| б) 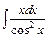 ; ;
|
в) 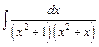 ; ;
| г) 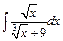 ; ;
| |
д) 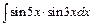 ; ;
| е) 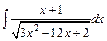 . .
| |
| 207. | a) 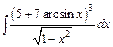 ; ;
| б) 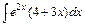 ; ;
|
в) 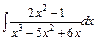 ; ;
| г) 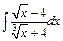 ; ;
| |
д) 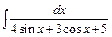 ; ;
| е) 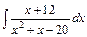 . .
| |
| 208. | a) 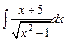 ; ;
| б) 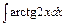 ; ;
|
в) 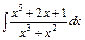 ; ;
| г) 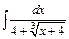 ; ;
| |
д) 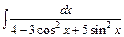 ; ;
| е) 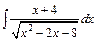 . .
| |
| 209. | a) 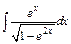 ; ;
| б) 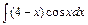 ; ;
|
в) 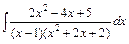 ; ;
| г) 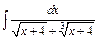 ; ;
| |
д) 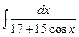 ; ;
| е) 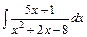 . .
| |
| 210. | a) 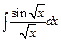 ; ;
| б) 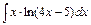 ; ;
|
в) 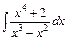 ; ;
| г) 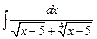 ; ;
| |
д) 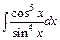 ; ;
| е) 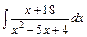 . .
|
211 – 220. Вычислить несобственный интеграл или доказать его расходимость.
| 211. | а) 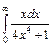 ; ;
| б). 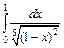 . .
|
| 212. | а) 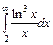 ; ;
| б). 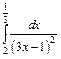 . .
|
| 213. | а) 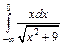 ; ;
| б). 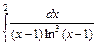 . .
|
| 214. | а) 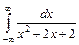 ; ;
| б). 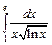 . .
|
| 215. | а) 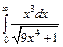 ; ;
| б). 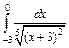 . .
|
| 216. | а) 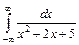 ; ;
| б). 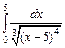 . .
|
| 217. | а) 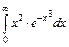 ; ;
| б). 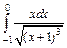 . .
|
| 218. | а) 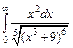 ; ;
| б). 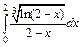 . .
|
| 219. | а) 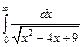 ; ;
| . б). 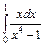 . .
|
| 220. | а) 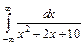 ; ;
| б). 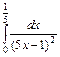 . .
|
221. Найти площадь фигуры, ограниченной параболой 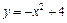 и прямой
и прямой 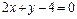 .
.
222. Найти площадь фигуры, ограниченной параболой 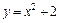 и прямой
и прямой 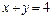 .
.
223. Найти длину дуги данной линии
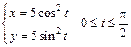 .
.
224. Вычислить объем тела, образованного вращением вокруг оси Ox кривой 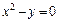 , x = –1, y = 0.
, x = –1, y = 0.
225. Вычислить площадь фигуры, ограниченной 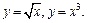
226. Вычислить длину дуги данной линии
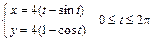 .
.
227. Вычислить объем тела, образованного вращением вокруг Oх кривой 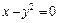 , x = 0, y = 1.
, x = 0, y = 1.
228. Найти длину кардиоиды 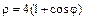 .
.
229. Вычислить объем тела, полученного вращением вокруг оси Оy фигуры, ограниченной парабалами 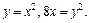
230. Найти длину дуги полукубической парабалы 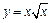 , концами которой являются точки с абсциссами
, концами которой являются точки с абсциссами 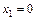 и
и 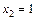 .
.
|
из
5.00
|
Обсуждение в статье: Элементы линейной алгебры. 51 – 60. Дана система линейных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

