Полные системы в основных классах двоичных функций

Утверждение 1:

Полной системой в классе Т₀ является система

Доказательство:

Обе функции принадлежат Т₀. Осталось показать, что , то есть любую 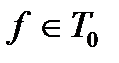можно представить суперпозицией функций

Рассмотрим и полином Жегалкина Тогда свободное слагаемое данного полинома равно 0 в силу того, что .Поэтому данный полином есть суперпозиция только . Это и есть требуемая суперпозиция.

Утвеждение 2:

В классе Т₁ полной является система .

Доказательство:

Рассмотрим . Покажем, что ее можно получить суперпозицией . В дальнейшем потребуются функции:

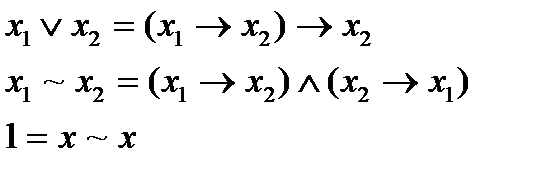
Рассмотрим функции (k+1 – число наборов, на которых f равна единице), которые получаются из по правилу:

для каждой функции оставляем соответствующий единичный набор, а на остальных (кроме 1…1) приравниваем к нулю.

Например:

0 0 0 0 0 0 0

0 0 1 0 0 0 0

0 1 0 1 1 0 0

0 1 1 0 0 0 0

1 0 0 1 0 1 0

1 0 1 1 0 0 1

1 1 0 0 0 0 0

1 1 1 1 1 1 1

В результате дополнительных функций будет столько, сколько единичных наборов без последнего. Очевидно

Поэтому, чтобы найти представление функции через достаточно найти представление каждой из добавочных функций через

Если f имеет один единичный набор,то это есть элементарная конъюнкция переменных без отрицания. В противном случае рассмотрим дополнительную функцию f_i . Не теряя общности будем считать, что соответствующий единичный набор имеет вид: . Тогда справедливо:

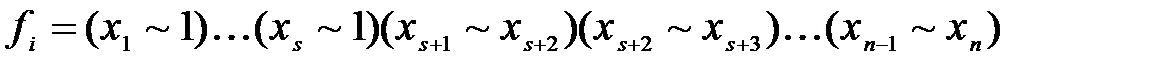
Например: f₁ равна 1 на наборах 010 и 111, поэтому

 

Утверждение 3:

В классе S полной является система

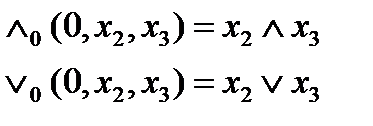
0 0 0 0 0

0 0 1 0 1

0 1 0 0 1

0 1 1 1 1

1 0 0 0 0

1 0 1 1 0

1 1 0 1 0

1 1 1 1 1

 

Все функции в данной системе являются самодвойственными. В дальнейшем потребуется - это самодвойственная фукция от 3-ех переменных, которая совпадает с логическим сложением на тех наборах, где первая переменная равна нулю (тогда на остальных наборах функция однозначно доопределяется по самодвойственности).

 

Самодвойственных функций, существенно зависящих от двух переменных нет:

0 0 01 0 1 1 0

0 1 01 0 1 0 1

1 0 10 1 0 1 0

1 1 10 1 0 0 1

 

 

Функции, не имеющие существенных переменных – константы, т.е. не самодвойственные функции от одной переменной есть .

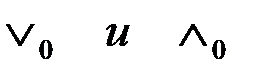коммутативные операции, относительно второй и третьей переменных при фиксированной первой:

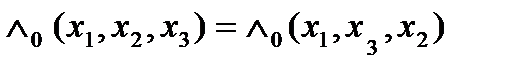
и ассоциативны относительно второй и третьей переменных при фиксированной первой:

Будем обозначать:

 

Из этих двух свойств следует что значение выражения, в котором присутствуют символы не зависят от порядка расположения скобок в нем и расположения множителей.

Например:

Выражение, в котором присутствует символ на наборах, в которых равно 1, тогда и только тогда, когда все переменные выражения равны 1: =0 и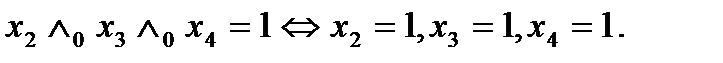

Значение выражения, в котором присутствует не зависит от расположения скобок и это выражение на наборах в которых равно 1, когда хотя бы одна из переменных равна 1.

Утверждение:

 

Например:

0 0 0 0

0 0 1 1

0 1 0 1

0 1 1 0

1 0 0 1

1 0 1 0

1 1 0 0

1 1 1 1

Доказательство:

Рассуждения в этом случае аналогичны случаю представления функции в виде СДНФ.Формальное доказательство следующее.

Заметим, что данное равенство достаточно показать только на первой половине наборов, где , тогда на оставшихся наборах равенство будет справедливо в силу самодвойственности функции в левой части и функции в правой части, как суперпозиция самодвойственных.

Рассмотрим набор

Покажем, что значение правой части на данных наборах равен 1 соответственно 0.

1) Рассмотрим слагаемые правой части, которые соответствуют набору .

Значение данного слагаемого на наборе равно 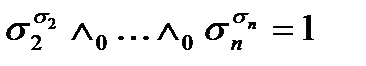, т.к. значение степени и основания совпадают, каждый множитель этого слагаемого равно 1, поэтому и все произведение равно1.

А поэтому значение всей дизъюнкции равно 1, т.к. существует слагаемое, равное 1.

2) . Рассмотрим произвольное слагаемое в правой части. Пусть оно соответствует единичному набору тогда наборы и различны, поэтому , тогда i-ый множитель на наборе будет равен 0, таким образом все слагаемые равны 0. Тогда значение всей правой части равно 0 на наборе . Утверждение доказано.

4) В классе монотонных функций полной является система .

Определение:

Нижней единицей монотонной функции называют набор значений переменных этой функции, на котором и для любого набора

Пример:

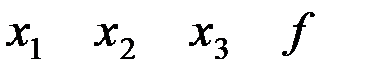
0 0 0 0

0 0 1 1

0 1 0 0

0 1 1 1

1 0 0 0

1 0 1 1

1 1 0 1

1 1 1 1

 

набор 001 для монотонной функции является нижней единицей набор 110 тоже нижняя единица функции .

 

Утверждение:

Пусть для монотонной функции 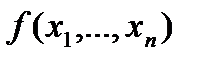: 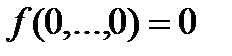, . Тогда справедливо представление:

Иначе говоря, для каждой нижней единицы записывается конъюнкция переменных, которые равны 1 в данном наборе, затем берем логическую сумму полученных слагаемых.

В данном примере разложение следующее: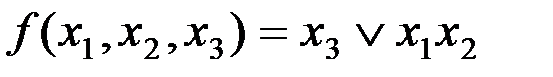

Доказательство:

1) тогда рассматриваем тот нижний набор, который меньше либо равен чем рассматриваемый , тогда в силу того, что в тех местах, где в наборе стоит 1, в также должна стоять 1.

Поэтому слагаемое, соответствующее набору равно 1 на наборе , а поэтому и вся дизъюнкция равна 1.

2)

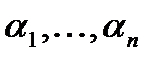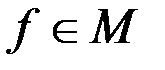Рассмотрим произвольное слагаемое, которое соответствует нижней единице , на наборе и покажем, что значение этого слагаемого равно 0 на наборе . Допустим противное, , что соответствующее слагаемое на наборе равно 1.Тогда в тех местах , где в наборе стоит 1 в наборе также стоит 1, то есть . Но в силу того, что получаем противоречие, т.к. значение 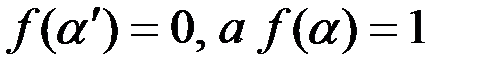, в то время как

5) В классе L полной системой является следующая .

Доказательство:

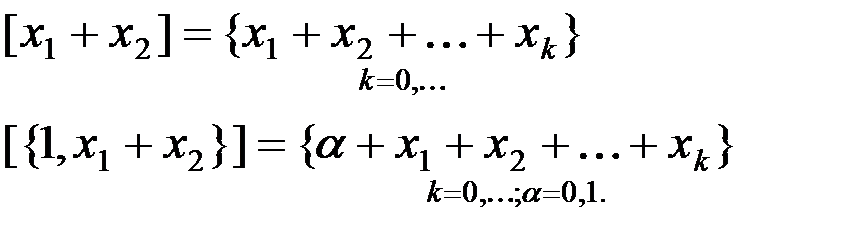
а это и есть все линейные функции.

 

 

Базисы в классах T₀ , T₁, S, M, L

Все полные системы для классов T₀, T₁, S, M, L в утверждениях выше являются базисами для этих систем.

Доказательство:

1) - эта система полна в Т₀ . Покажем, что любая собственная подсистема полной в Т₀ не является. Рассмотрим . Т.к. ,тогда , но функция не является полной в классе Т₀ .

Рассмотрим в силу того, что не является полной в классе Т₀ . Таким образом все собственные подсистемы не полны в классе Т₀, поэтому - базис в Т₀ .

2) - эта система полна в Т₁ . Покажем, что все собственные подсистемы не полны в Т₁. Покажем, что не полна в Т₁ , а именно . Для этого рассмотрим класс К следующих функций: , если и только если для любых 2-х наборов значений переменных, на которых значение функции равно 0 существует переменная равная 0 в обоих наборах, причем наборы не обязательно различные:

Например

 

0 0 1 1 0 0

0 1 1 1 0 0

1 0 0

1 1 1 в обоих наборах.

Из определения следует, что на единичном наборе функция из К равна единице.

 

0 0 0

0 1 1

1 0 1 0 0 в обоих наборах

1 1 1 0 0

 

0 0 0

0 1 0 0 1

1 0 0 1 0

1 1 1

 

Утверждение:

Класс К замкнут относительно суперпозиции функций.

Доказательство: Пусть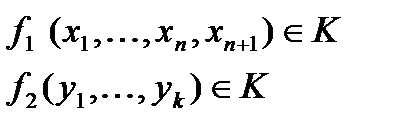

 

Образуем их суперпозицию:

Пусть верно противное - суперпозиция , тогда существует пара наборов значений переменных

:

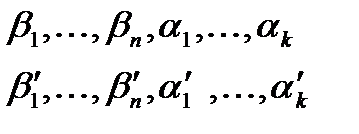для любого 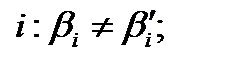и для любого

Обозначим

.

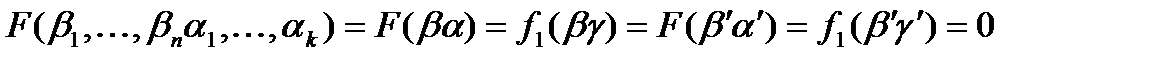Тогда на обоих наборах 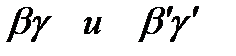значение равно 0. В силу того, что , и т.к. в наборах нет переменной, равной нулю, такой переменной должна быть последняя переменная , т. е. . Но для наборов нет переменной, равной нулю в обоих наборах, следовательно получаем противоречие с тем, что . Утверждение доказано.

В силу того, что . Но .

 

Рассмотрим в силу того, что , имеем, . Таким образом все собственные подсистемы системы полными в Т₁ не являются, и тогда является базисом в Т₁ .

2) есть базис в S. Эта система полна в классе S. Покажем, что все собственные подсистемы данной системы в классе S полными не являются - эта функции у которых ровно одна существенная переменная, а функция имеет три существенные переменные. Поэтому .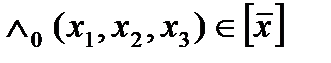

3) Рассмотрим функцию

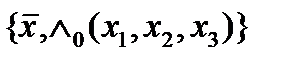, поэтому система - базис в S .

4) Покажем, что - базис в М. Во-первых эта система полна в классе М . Покажем, что все собственные подсистемы не полные.

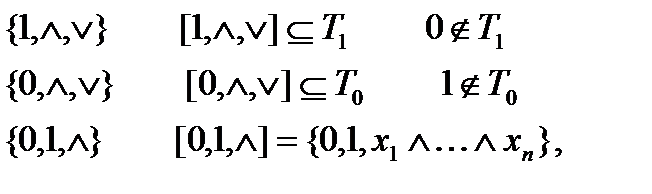
а функции дизъюнкции в замыкании нет поэтому система не полна в классе М.

, а функции в замыкании нет, следовательно система не полна в классе М следовательно начальная система есть базис в классе монотонных функций.

5) Система полна в классе L . Покажем, что все собственные подсистемы в классе линейных полными не являются:

следовательно начальная система 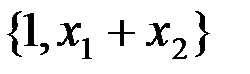является базисом в классе линейных функций.

Замечание

Вопросы о представлении функций в монотонном базисе потребуются в следующем разделе минимизации двоичных фукций.

Замечание

Пост нашел все замкнутые классы в классе двоичных функций и описал структуру их взаимных вложений.

 

2 .Минимизация ДНФ заданной функции.

Пример.

Рассмотрим функцию от десяти переменных, которая равна 0 только на одном наборе (нулевом). На всех остальных наборах значение функции равно 1.

Если рассмотреть данную функцию в виде СДНФ, то длина записи СДНФ, т.е. общее число вхождений переменных, равна (2¹⁰-1)10 .

 

2¹⁰-1 — это число единиц функции, т.е. число слагаемых в СДНФ функции f, и каждое слагаемое содержит десять множителей, поэтому общее число вхождений переменных равно числу переменных в каждом слагаемом, умноженное на число слагаемых

 

(2¹⁰-1)10 = 10230

 

Рассмотрим представление данной функции в СКНФ :x₁Ú ... Ú x₁₀ .Тогда длина СКНФ равна 10.

 

Определение :ДНФ называем функцию вида дизъюнкции некоторого количества слагаемых, где каждое слагаемое есть элементарная конъюнкция.

 

Например:x₁ Ú x₃ x₄ Ú x₁ x₃ Ú x₁ x₄ x₂

 

Определение:Скажем, что ДНФ представляет функцию f, если ДНФ совпадает тождественно с функцией f.

Определение:Рангом элементарной конъюнкции называют число множителей в ней.

Определение:Сложностью ДНФ называют сумарный ранг конъюнкций, которые входят в данную ДНФ .

S (...)=2 + 2 + 3 + 3 = 10

Определение:Минимальной ДНФ функции f называют ДНФ, которая представляет функцию f и обладает наименьшей сложностью.

Определение:Кратчайшей ДНФ функции f называют ДНФ, которая представляет функцию f и содержит наименьшее число элементарных конъюнкций.

 

Пример:

x₁ x₂ f

0 0 0

0 1 1

1 0 1

1 1 1

 

Рассмотрим x₁ Ú x₂ ; не трудно видеть : ДНФ x₁Ú x₂ является одновременно минимальной и кратчайшей. Данная ДНФ представляет функцию f и обладает наименьшей сложностью, сложность равна 2, т.к. число элементарных конъюнкций равно 2, каждая из которых имеет ранг 1. ДНФ меньшей сложности не может представлять данную функцию, т.к. данная функция имеет две существенные переменные, а ДНФ сложности 1 и меньше имеет не более одной существенной переменной. Данная ДНФ является кратчайшей, т.к. она содержит две элементарные конъюнкции, а ДНФ с меньшим числом элементарных конъюнкций от двух существенных переменных имеют следующий вид: x₁ x₂ x₁ 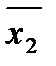x₂ .

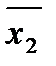Все перечисленные функции имеют всего лишь одну единицу. x₁ Ú x₂ имеют три единицы.