 |
Главная |
Найти функцию распределения F(x)
|
из
5.00
|
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Пример 2.1. Случайная величина X задана функцией распределения

Найти вероятность того, что в результате испытания X примет значения, заключенные в промежутке (2,5; 3,6).
Решение:Вероятность попадания величины Х в промежуток (2,5; 3,6) можно определить двумя способами:
1.  .
.
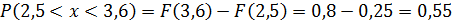 .
.
или
2.  .
.
 .
.
Ответ:  .
.
Пример 2.2. При каких значениях параметров А и В функция F(x) = A + Be-x может быть функцией распределения для неотрицательных значений случайной величины Х.
Решение: Так как все возможные значения случайной величины Х принадлежат интервалу  , то для того, чтобы функция
, то для того, чтобы функция  была функцией распределения для Х, должно выполняться свойство:
была функцией распределения для Х, должно выполняться свойство:
 .
.
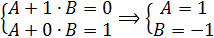 .
.
Ответ: 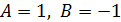 .
.
Пример 2.3. Случайная величина X задана функцией распределения

Найти вероятность того, что в результате четырех независимых испытаний величина X ровно 3 раза примет значение, принадлежащее интервалу (0,25;0,75).
Решение:Вероятность попадания величины Х в промежуток (0,25;0,75) найдем по формуле:
 .
.
 .
.
Далее вероятность того, что в результате четырех независимых испытаний величина X ровно 3 раза примет значение, принадлежащее данному интервалу, вычисляется по формуле Бернулли:
 .
.
 .
.
Ответ:  .
.
Пример 2.4. Вероятность попадания мячом в корзину при одном броске равна 0,3. Составить закон распределения числа попаданий при трех бросках.
Решение: Случайная величина Х – число попаданий в корзину при трех бросках – может принимать значения: 0, 1, 2, 3. Вероятности того, что Х примет эти значения, найдем по формуле Бернулли:
 .
.
 .
.
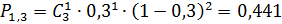 .
.
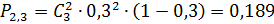 .
.
 .
.
Таким образом, получаем следующий закон распределения вероятностей случайной величины Х:

| ||||

| 
| 
| 
| 
|
Пример 2.5. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,5, вторым – 0,4. Составить закон распределения числа попаданий в мишень.
Решение: Найдем закон распределения дискретной случайной величины Х – числа попаданий в мишень. Пусть событие  – попадание в мишень первым стрелком, а
– попадание в мишень первым стрелком, а  – попадание вторым стрелком,
– попадание вторым стрелком,  и
и 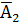 - соответственно их промахи.
- соответственно их промахи.
 .
.
 .
.
 .
.
Составим закон распределения вероятностей СВ Х:

| |||

| 
| 
| 
|
Пример 2.6. Испытываются 3 элемента, работающих независимо друг от друга. Длительности времени (в часах) безотказной работы элементов имеют функции плотности распределения: для первого: F1(t) =1-e-0,1t , для второго: F2(t) = 1-e-0,2t , для третьего: F3(t) =1-e-0,3t . Найти вероятность того, что в интервале времени от 0 до 5 часов: откажет только один элемент; откажут только два элемента; откажут все три элемента.
Решение: Воспользуемся определением производящей функции вероятностей  :
:
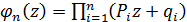 ,
,
где  .
.
Вероятность  того, что в
того, что в  независимых испытаниях, в первом из которых вероятность появления события А равна
независимых испытаниях, в первом из которых вероятность появления события А равна  , во втором
, во втором  и т. д., событие А появится ровно
и т. д., событие А появится ровно  раз, равна коэффициенту при
раз, равна коэффициенту при  в разложении производящей функции по степеням
в разложении производящей функции по степеням  . Найдем вероятности отказа и неотказа соответственно первого, второго и третьего элемента в интервале времени от 0 до 5 часов:
. Найдем вероятности отказа и неотказа соответственно первого, второго и третьего элемента в интервале времени от 0 до 5 часов:
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
Составим производящую функцию:
 .
.
Коэффициент при  равен вероятности
равен вероятности  того, что событие А появится ровно три раза, то есть вероятности отказа всех трех элементов; коэффициент при
того, что событие А появится ровно три раза, то есть вероятности отказа всех трех элементов; коэффициент при  равен вероятности
равен вероятности  того, что откажут ровно два элемента; коэффициент при
того, что откажут ровно два элемента; коэффициент при  равен вероятности
равен вероятности  того, что откажет только один элемент.
того, что откажет только один элемент.
Ответ: 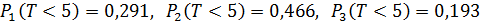 .
.
Пример 2.7. Дана плотность вероятности f(x)случайной величины X:

Найти функцию распределения F(x).
Решение: Используем формулу:
 .
.
При  .
.
При  .
.
При  .
.
Таким образом, функция распределения имеет вид:

Пример 2.8. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
Решение: Случайная величина Х – число элементов, отказавших в одном опыте – может принимать значения: 0, 1, 2, 3. Вероятности того, что Х примет эти значения, найдем по формуле Бернулли:
 .
.
 .
.
 .
.
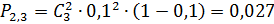 .
.
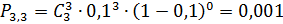 .
.
Таким образом, получаем следующий закон распределения вероятностей случайной величины Х:

| ||||

| 
| 
| 
| 
|
Пример 2.9. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения числа стандартных деталей среди отобранных.
Решение:Случайная величина Х – число стандартных деталей среди отобранных – может принимать значения: 1, 2, 3 и имеет гипергеометрическое распределение. Вероятности того, что Х примет эти значения, найдем по формуле:

где  -- число деталей в партии;
-- число деталей в партии;
 -- число стандартных деталей в партии;
-- число стандартных деталей в партии;
 – число отобранных деталей;
– число отобранных деталей;
 -- число стандартных деталей среди отобранных.
-- число стандартных деталей среди отобранных.
 .
.
 .
.
 .
.
Тогда закон распределения случайной величины  будет такой:
будет такой:

| |||

| 
| 
| 
|
Пример 2.10. Случайная величина  имеет плотность распределения
имеет плотность распределения

причем  и
и  не известны, но
не известны, но  , а
, а  и
и  . Найдите
. Найдите  и
и  .
.
Решение: В данном случае случайная величина X имеет треугольное распределение (распределение Симпсона) на отрезке [a, b]. Числовые характеристики X :
 .
.
 .
.
Следовательно,  . Решая данную систему, получим две пары значений:
. Решая данную систему, получим две пары значений:  . Так как по условию задачи
. Так как по условию задачи  , то окончательно имеем:
, то окончательно имеем:  .
.
Ответ:  .
.
Пример 2.11. В среднем по 10% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Вычислить математическое ожидание и дисперсию числа таких договоров среди наудачу выбранных четырех.
Решение:Математическое ожидание и дисперсию можно найти по формулам:
 .
.
 .
.
Возможные значения СВ  (число договоров (из четырех) с наступлением страхового случая): 0, 1, 2, 3, 4.
(число договоров (из четырех) с наступлением страхового случая): 0, 1, 2, 3, 4.
Используем формулу Бернулли, чтобы вычислить вероятности различного числа договоров (из четырех), по которым были выплачены страховые суммы:
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
Ряд распределения СВ  (число договоров с наступлением страхового случая) имеет вид:
(число договоров с наступлением страхового случая) имеет вид:

| |||||

| 0,6561 | 0,2916 | 0,0486 | 0,0036 | 0,0001 |
Теперь вычислим числовые характеристики величины  :
:
 .
.
 .
.
Ответ:  ,
,  .
.
Пример 2.12. Из пяти роз две белые. Составить закон распределения случайной величины, выражающей число белых роз среди двух одновременно взятых.
Решение:В выборке из двух роз может либо не оказаться белой розы, либо может быть одна или две белые розы. Следовательно, случайная величина Х может принимать значения: 0, 1, 2. Вероятности того, что Х примет эти значения, найдем по формуле:

где 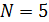 -- число роз;
-- число роз;
 -- число белых роз;
-- число белых роз;
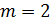 – число одновременно взятых роз;
– число одновременно взятых роз;
 -- число белых роз среди взятых.
-- число белых роз среди взятых.
 .
.
 .
.
 .
.
Тогда закон распределения случайной величины  будет такой:
будет такой:

| |||

| 
| 
| 
|
Пример 2.13. Среди 15 собранных агрегатов 6 нуждаются в дополнительной смазке. Составить закон распределения числа агрегатов, нуждающихся в дополнительной смазке, среди пяти наудачу выбранных из общего числа.
Решение:Случайная величина Х – число агрегатов, нуждающихся в дополнительной смазке среди пяти выбранных – может принимать значения: 0, 1, 2, 3, 4, 5 и имеет гипергеометрическое распределение. Вероятности того, что Х примет эти значения, найдем по формуле:

где  -- число собранных агрегатов;
-- число собранных агрегатов;
 -- число агрегатов, нуждающихся в дополнительной смазке;
-- число агрегатов, нуждающихся в дополнительной смазке;
 – число выбранных агрегатов;
– число выбранных агрегатов;
 -- число агрегатов, нуждающихся в дополнительной смазке среди выбранных.
-- число агрегатов, нуждающихся в дополнительной смазке среди выбранных.
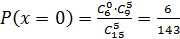 .
.
 .
.
 .
.
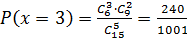 .
.
 .
.
 .
.
Тогда закон распределения случайной величины  будет такой:
будет такой:

| ||||||

| 
| 
| 
| 
| 
| 
|
Пример 2.14. Из поступивших в ремонт 10 часов 7 нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы, прекращает дальнейший просмотр. Найти математическое ожидание и дисперсию числа просмотренных часов.
Решение: Случайная величина Х – число агрегатов, нуждающихся в дополнительной смазке среди пяти выбранных – может принимать значения: 1, 2, 3, 4. Вероятности того, что Х примет эти значения, найдем по формуле:

 .
.
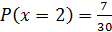 .
.
 .
.
 .
.
Тогда закон распределения случайной величины  будет такой:
будет такой:

| ||||

| 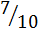
| 
| 
| 
|
Теперь вычислим числовые характеристики величины  :
:
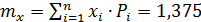 .
.
 .
.
Ответ: 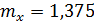 ,
,  .
.
Пример 2.15. Абонент забыл последнюю цифру нужного ему номера телефона, однако помнит, что она нечетная. Найти математическое ожидание и дисперсию числа сделанных им наборов номера телефона до попадания на нужный номер, если последнюю цифру он набирает наудачу, а набранную цифру в дальнейшем не набирает.
Решение: Случайная величина  может принимать значения:
может принимать значения:  . Так как набранную цифру абонент в дальнейшем не набирает, то вероятности этих значений равны
. Так как набранную цифру абонент в дальнейшем не набирает, то вероятности этих значений равны  .
.
Составим ряд распределения случайной величины:

| |||||

| 0,2 | 
| 
| 
| 
|
Вычислим математическое ожидание и дисперсию числа попыток набора номера:
 .
.
 .
.
Ответ:  ,
,  .
.
Пример 2.16. Вероятность отказа за время испытаний на надежность для каждого прибора серии равна p. Определить математическое ожидание числа приборов, давших отказ, если испытанию подверглись N приборов.
Решение:Дискретная случайная величина X — число отказавших приборов в N независимых испытаниях, в каждом из которых вероятность появления отказа равна p, распределена по биномиальному закону. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:
 .
.
Ответ:  .
.
Пример 2.17. Дискретная случайная величина X принимает 3 возможных значения:  с вероятностью
с вероятностью  ;
;  с вероятностью
с вероятностью  и
и  с вероятностью
с вероятностью 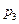 . Найти
. Найти  и
и 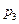 , зная, что M(X) = 8.
, зная, что M(X) = 8.
Решение: Используем определения математического ожидания и закона распределения дискретной случайной величины:


Находим:  .
.
 .
.
Ответ:  .
.
Пример 2.18. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. В каждой партии содержится 5 изделий. Найти математическое ожидание случайной величины X – числа партий, в каждой из которых содержится ровно 4 стандартных изделия, если проверке подлежат 50 партий.
Решение: В данном случае все проводимые опыты независимы, а вероятности того, что в каждой партии содержится ровно 4 стандартных изделия, одинаковы, следовательно, математическое ожидание можно определить по формуле:
 ,
,
где  - число партий;
- число партий;
 - вероятность того, что в партии содержится ровно 4 стандартных изделия.
- вероятность того, что в партии содержится ровно 4 стандартных изделия.
Вероятность  найдем по формуле Бернулли:
найдем по формуле Бернулли:
 .
.
 .
.
 .
.
Ответ:  .
.
Пример 2.19. Найти дисперсию случайной величины X – числа появлений события A в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что M(X) = 0,9.
Решение: Задачу можно решить двумя способами.
1) Возможные значения СВ X : 0, 1, 2. По формуле Бернулли определим вероятности этих событий:
 .
.
 ,
,  ,
,  .
.
Тогда закон распределения X имеет вид:

| |||

| 
| 
| 
|
Из определения математического ожидания определим вероятность  :
:
 .
.
Найдем дисперсию СВ X:
 .
.
 .
.
2) Можно использовать формулу:
 .
.
 .
.
 .
.
Ответ:  .
.
Пример 2.20. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15; 25).
Решение: Вероятность попадания нормальной случайной величины Х на участок от  до
до  выражается через функцию Лапласа:
выражается через функцию Лапласа:
 .
.
 .
.
Ответ:  .
.
Пример 2.21. Дана функция: 
При каком значении параметра C эта функция является плотностью распределения некоторой непрерывной случайной величины X? Найти математическое ожиданий и дисперсию случайной величины X.
Решение:Для того, чтобы функция  была плотностью распределения некоторой случайной величины
была плотностью распределения некоторой случайной величины  , она должна быть неотрицательна, и она должна удовлетворять свойству:
, она должна быть неотрицательна, и она должна удовлетворять свойству:
 .
.
Следовательно:
 .
.
Вычислим математическое ожидание по формуле:
 .
.
 .
.
Вычислим дисперсию по формуле:
 .
.
 .
.
Ответ:  ,
,  ,
,  .
.
Пример 2.22. Величина X задана плотностью вероятности  в интервале (0;1), вне этого интервала
в интервале (0;1), вне этого интервала  . Найти: постоянный параметр С; математическое ожидание величины X.
. Найти: постоянный параметр С; математическое ожидание величины X.
Решение: Воспользуемся свойством плотности распределения случайной величины  :
:
 .
.
Следовательно:
 .
.
Вычислим математическое ожидание по формуле:
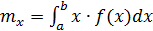 .
.
 .
.
Ответ:  ,
,  .
.
Пример 2.23. Случайная величина X в интервале (0;  ) задана плотностью вероятности
) задана плотностью вероятности  ; вне этого интервала
; вне этого интервала  . Найти дисперсию X.
. Найти дисперсию X.
Решение:Найдем математическое ожидание и дисперсию СВ X по следующим формулам:
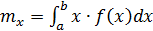 .
.
 .
.
 .
.
 .
.
Ответ:  .
.
Пример 2.24. Устройство состоит из N элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна p. Необходимо найти математическое ожидание и дисперсию этой случайной величины.
Решение: Закон распределения дискретной случайной величины X — числа появлений события в  независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна  , называют биномиальным. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события А одном испытании:
, называют биномиальным. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события А одном испытании:
 .
.
Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:

Пример 2.25. Производится три независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0.25. Определить среднее квадратическое отклонение числа попаданий при трех выстрелах.
Решение: Так как производится три независимых испытания, и вероятность появления события А (попадания) в каждом испытании одинакова, то будем считать, что дискретная случайная величина X — число попаданий в мишень – распределена по биномиальному закону.
Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:


Ответ: 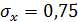 .
.
Пример 2.26. Среднее число клиентов, посещающих страховую компанию за 10 мин., равно трем. Найти вероятность того, что в ближайшие 5 минут придет хотя бы один клиент.
Решение:Будем считать, что число клиентов на любом участке времени распределено по закону Пуассона.
Среднее число клиентов, пришедших за 5 минут:  .
.
Вероятность того, что придет хотя бы один клиент:
 .
.
Ответ:  .
.
Пример 2.27. Среднее время настройки прибора составляет 5 минут и подчинено показательному распределению. Мастер уже потратил 5 минут на настройку очередного прибора. Найти вероятность того, что он затратит еще не менее трех минут на настройку этого прибора.
Решение: Запишем закон распределения времени настройки  прибора в виде
прибора в виде 
С учетом того фактора, что  , имеем усеченное показательное распределение в виде
, имеем усеченное показательное распределение в виде  , где параметр
, где параметр 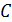 определяется из соотношения
определяется из соотношения  .
.
Для нашего случая  .
.
Получаем усеченное распределение в виде  .
.
Тогда искомую вероятность найдем по соотношению

Ответ:  .
.
Пример 2.28. В отдел заказов в среднем приходит 18 клиентов в час. Определить вероятность того, что за две текущие минуты в отдел заказов придет хотя бы один клиент.
Решение: Будем считать, что число клиентов на любом участке времени распределено по закону Пуассона.
Среднее число клиентов, пришедших за 2 минуты:  .
.
Вероятность того, что придет хотя бы один клиент:
 .
.
Ответ:  .
.
Пример 2.29. Время ожидания заявки в очереди на процессор подчиняется показательному закону распределения со средним значением 20 секунд. Найти вероятность того, что очередная (произвольная) заявка будет ожидать процессор более 35 секунд.
Решение: В этом примере математическое ожидание  , а интенсивность отказов равна
, а интенсивность отказов равна  .
.
Тогда искомая вероятность: 
Ответ:  .
.
Пример 2.30. Группа студентов в количестве 15 человек проводит собрание в зале, в котором 20 рядов по 10 мест в каждом. Каждый студент занимает место в зале случайным образом. Какова вероятность того, что не более трех человек будут находиться на седьмом месте ряда?
Решение:
Пример 2.31. В партии из 10 деталей имеется 3 нестандартных. Составить закон распределения дискретной случайной величины Х - числа нестандартных деталей среди трех отобранных и найти ее математическое ожидание.
Решение: Дискретная случайная величина  – число нестандартных деталей среди трех отобранных - может принимать значения:
– число нестандартных деталей среди трех отобранных - может принимать значения:  .
.
Общее число способов выбора трех деталей из десяти определяется числом сочетаний  . Число способов выбора трех деталей, среди которых
. Число способов выбора трех деталей, среди которых  нестандартных, а
нестандартных, а  - стандартных деталей (
- стандартных деталей (  , определяем по правилу произведения как
, определяем по правилу произведения как  .
.
Тогда согласно классическому определению вероятности:

где 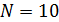 -- число деталей в партии;
-- число деталей в партии;
 -- число нестандартных деталей в партии;
-- число нестандартных деталей в партии;
 – число отобранных деталей;
– число отобранных деталей;
 -- число нестандартных деталей среди отобранных.
-- число нестандартных деталей среди отобранных.
 .
.
 .
.
 .
.
 .
.
Тогда закон распределения случайной величины  будет такой:
будет такой:
|
из
5.00
|
Обсуждение в статье: Найти функцию распределения F(x) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы
(0.008 сек.)

