 |
Главная |
Разрыв с конечным скачком
|
из
5.00
|
Раздел 7. Непрерывность функции в точке. Классификация точек разрыва.
1. Понятие непрерывной функции
2. Устранимый разрыв:
3. Разрыв с конечным скачком.
4. Разрыв с бесконечным скачком
5. Важное свойство функций, непрерывных на промежутке
Понятие непрерывной функции
В предыдущих параграфах мы познакомились с важнейшим понятием математического анализа – пределом функции. При этом  мы могли вычислять и в том случае, когда
мы могли вычислять и в том случае, когда  существует, и в том случае, когда
существует, и в том случае, когда  не существует. Изучим подробнее эти два случая.
не существует. Изучим подробнее эти два случая.
Определение. Функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если  определена в этой точке, т.е.
определена в этой точке, т.е.  существует, причём
существует, причём
 (1)
(1)
т.е. «предел функции в точке равен значению функции в этой точке».
Определение. Функция называется непрерывной на интервале  , если она непрерывна во всех точках этого интервала.
, если она непрерывна во всех точках этого интервала.
Непрерывность является важнейшим свойством функций. Если равенство (1) не выполняется, то функция называется разрывной в точке 
Для того, чтобы лучше усвоить понятие непрерывности функции в точке, рассмотрим все случаи нарушения непрерывности или, как говорят, проведём классификацию точек разрыва.
Сначала отметим теорему: все элементарные функции непрерывны в своей области определения. Элементарными функциями называются упомянутые нами три класса функций, включая и их различные комбинации.Например, функция  элементарная функция.
элементарная функция.
Исследование на непрерывность элементарных функций, в соответствии с последней теоремой, начинаем с нахождения области определения - находим точки, в которых функция не определена, следовательно, разрывна. Далее выясняем вид разрыва (или, как говорят, характер равенства).
2. Устранимый разрыв:
Функция  не определена в точке
не определена в точке  , но
, но  существует и конечный.
существует и конечный.
Пример 1: 
Ясно, что  - не существует, но по первому замечательному пределу
- не существует, но по первому замечательному пределу 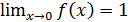 . Для наглядности нетрудно построить график этой функции:
. Для наглядности нетрудно построить график этой функции:






 1
1
 |
-2 
 0
0  2
2  3
3  х
х
Рис. 1
График пересекает ось  в точках
в точках  постепенно «затухая». При приближении к нулю (предел!) обе ветви «стремятся» к точке
постепенно «затухая». При приближении к нулю (предел!) обе ветви «стремятся» к точке  , но в самой точке функция не определена (для обозначения этого факта поставим стрелки – точка выкалывается).
, но в самой точке функция не определена (для обозначения этого факта поставим стрелки – точка выкалывается).
 Получается, что этот разрыв можно устранить – надо восстановить выколотую точку. Другими словами, функция
Получается, что этот разрыв можно устранить – надо восстановить выколотую точку. Другими словами, функция 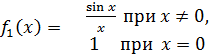 уже будет непрерывной.
уже будет непрерывной.
Разрыв с конечным скачком.
 Сначала построим график функции (рис.2)
Сначала построим график функции (рис.2) 





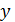

 1
1



0 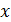 0 1
0 1 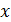

 -1
-1
Рис. 2 Рис. 3
Видим, что функция (благодаря присутствия модуля) задаётся двумя аналитическими выражениями:  при
при  и
и  при
при  График состоит из двух ветвей.
График состоит из двух ветвей.
Ещё пример: при вычислении пределов мы писали:  .
.
Однако, легко построить график функции  (рис. 3) и увидеть, что при
(рис. 3) и увидеть, что при  левая ветвь уходит вниз (стремится к минус бесконечности), а правая ветвь уходит вверх (стремится к плюс бесконечности). Таким образом, желательно уточнять знак бесконечности. С этой целью вводятся понятия односторонних (левосторонних и правосторонних) пределов.
левая ветвь уходит вниз (стремится к минус бесконечности), а правая ветвь уходит вверх (стремится к плюс бесконечности). Таким образом, желательно уточнять знак бесконечности. С этой целью вводятся понятия односторонних (левосторонних и правосторонних) пределов.
Определение. Рассмотрим 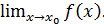 Пусть аргумент
Пусть аргумент 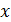 стремится к числу
стремится к числу  слева, т.е. оставаясь всё время меньше
слева, т.е. оставаясь всё время меньше  Такой предел называется левосторонним и обозначается
Такой предел называется левосторонним и обозначается 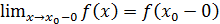 .
.
Аналогично определяется правосторонний предел  или
или  .Совершенно понятно, что если
.Совершенно понятно, что если  существует, т.е. равен числу, то оба односторонних предела существуют и равны. Поэтому получаем определение непрерывности в равносильной форме:
существует, т.е. равен числу, то оба односторонних предела существуют и равны. Поэтому получаем определение непрерывности в равносильной форме:
Функция 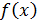 называется непрерывной в точке
называется непрерывной в точке  , если
, если  (3)
(3)
или более компактно  – если «предел слева равен пределу справа и равен значению функции в данной точке».
– если «предел слева равен пределу справа и равен значению функции в данной точке».
Определение (3) является самым удобным для классификации точек разрыва.
Определение. Если оба односторонних предела в точке  существуют, т.е. равны конечным числам, но не равны, то
существуют, т.е. равны конечным числам, но не равны, то  называется точкой разрыва I рода с конечным скачком, а разность
называется точкой разрыва I рода с конечным скачком, а разность  называется скачком функции в данной точке.
называется скачком функции в данной точке.
 Пример 2. Исследовать на непрерывность функцию
Пример 2. Исследовать на непрерывность функцию

Решение. Мы видим, что функция 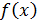 задана несколькими аналитическими выражениями. По этой причине она не является элементарной функцией - она составлена из трёх частей элементарных функций. Как говорят, она склеена из трёх ветвей элементарных функций.
задана несколькими аналитическими выражениями. По этой причине она не является элементарной функцией - она составлена из трёх частей элементарных функций. Как говорят, она склеена из трёх ветвей элементарных функций.
Каждая из функций, входящих в задание функции 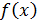 является элементарной, причём всюду непрерывной функцией. Поэтому точками, «подозрительными» на разрыв, являются точки, в которых функция меняет своё аналитическое выражение (иначе говоря, точки «склеивания» функций). В нашем примере таких точек две:
является элементарной, причём всюду непрерывной функцией. Поэтому точками, «подозрительными» на разрыв, являются точки, в которых функция меняет своё аналитическое выражение (иначе говоря, точки «склеивания» функций). В нашем примере таких точек две:  и для каждой из них проверяем условия непрерывности (3).
и для каждой из них проверяем условия непрерывности (3).

Имеем в точке  разрыв с конечным скачком, скачок
разрыв с конечным скачком, скачок  (см. рис.4).
(см. рис.4).
Исследуем 


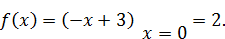
По определению (3) функция в точке  непрерывна.
непрерывна.
Нетрудно построить график этой функции (рис. 4).
Мы рекомендуем такие примеры начинать с построения графика функции, и по графику проверять своё исследование на непрерывность.



| |












 2 -x+3
2 -x+3

|




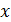


 0 1 2 3
0 1 2 3

 1
1

Рис. 4
|
из
5.00
|
Обсуждение в статье: Разрыв с конечным скачком |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


