Уравнение для собственных функций

Рассмотрим некоторую физическую величину (или, что то же самое, динамическую переменную) A, которой соответствует эрмитовый оператор . Будем считать, что спектр ее собственных значений — дискретный. Пусть An — собственные значения данной физической величины. Согласно постулату об измерении динамических переменных (см. стр. 26), в произвольном квантовом состоянии измерения будут давать значения An с некоторыми вероятностями. Поставим следующие вопросы:

1) Существует ли такое квантовое состояние, в котором многократные измерения данной физической величины дают одно и то же собственное значение An?

2) Если такое квантовое состояние существует, то как найти соответствующую волновую функцию?

3) Как найти вероятности появлений собственных значений данной физической величины при ее многократном измерении в произвольном квантовом состоянии?

Квантовое состояние, в котором многократные измерения физической величины A всегда дают значение An, называется собственным состоянием, отвечающим этому значению, а соответствующая волновая функция называется собственной волновой функцией (или просто собственной функцией). Cобственные функции физических величин будем обозначать строчной буквой , чтобы подчеркнуть, что эти функции зависят от координат частицы, но не зависят от времени. Заглавной буквой будут обозначаться волновые функции частицы, зависящие от времени и удовлетворяющие уравнению Шредингера (3.3).

• Покажем, что собственные функции любой физической величины находятся как решения уравнения

где A — постоянная. Собственные значения An физической величины есть те значения постоянной A, при которых уравнение (5.1) имеет решения ψn, удовлетворяющие требуемым условиям1.

(1Собственные функции должны быть непрерывными и однозначными. Для некоторых динамических переменных собственные функции должны быть периодическими. В других случаях необходимо потребовать, чтобы любая собственная функция стремилась к нулю на бесконечности. Подчеркнем, что дополнительные условия, которым должны удовлетворять собственные функции, формулируются, исходя из физического смысла динамической переменной.)

Предположим, что является решением уравнения (5.1), т. е.

Предположим также, что ψn нормирована на единицу [см. (2.25)]

Вычислим среднее значение физической величины в этом состоянии:

Мы видим, что . Это, однако, еще не означает, что в состоянии многократные измерения будут всегда давать значение An. Нужно также убедиться, что квантовая неопределенность данной физической величины в состоянии равна нулю. Вспоминая формулу (4.21)

, запишем

Мы доказали, что если волновая функция удовлетворяет уравнению (5.2), то в этом состоянии физическая величина A имеет определенное значение An. Можно доказать и обратное утверждение: если физическая величина в состоянии с волновой функцией имеет определенное значение An, то эта волновая функция удовлетворяет уравнению (5.2). Предлагаем читателю попытаться самостоятельно построить соответствующее доказательство.

Итак, спектр любой динамической переменной Aˆи собственные волновые функции можно найти, решив уравнение (5.1), которое, таким образом, играет исключительно важную роль в квантовой механике.

Из приведенных выше рассуждений следуют важные выводы, относящиеся к стационарным состояниям частицы и уравнению Шредингера (3.15)

для этих состояний:

В стационарном состоянии энергия имеет точное значение E.

Собственные значения гамильтониана частицы в заданном внешнем поле .образуют спектр значений энергии

В самом деле, стационарное уравнение Шредингера (3.15) есть частный случай общего уравнения (5.1) для собственных функций. Роль оператора 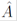играет гамильтониан — оператор энергии.