Конструирование функционала – критерия оптимальности

Курсовая работа

 

по дисциплине: «Методы решения задач

оптимального управления»

 

Выполнил:

 

Проверил: О.Ю.Торгашова

 

Саратов 2011 г.

 

Содержание.

Содержание______________________2

Оптимальное управление в RL – цепи ________________________________4

1.1. Описание объекта управления ______4

1.2. Конструирование функционала – критерия оптимальности______________4

1.3. Формулировка задачи как вариационной задачи на услов­ный экстремум __5

1.4. Синтез оптимального алгоритма управления__________________________5

1.5. Анализ процессов в системе _______10

1.6. Сравнительная оценка процессов в схеме при оптимальном и линейном режимах _______________________ 13

 

Заключение _______________________ 14

Литература _______________________ 15

 

Задача№1.

Исходные данные:

Электрическая схема, содержащая источник питания e(t), активные сопротивления r и R, индуктивность L.

R=45(Ом);

r=1,5(Ом);

L=0.018(Гн);

i(to)=0,3(A);

i(t1)=0,95(A);

 

 

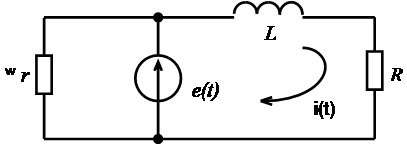Рис.1

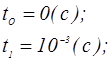
Найти:

а) определить оптимальный закон изменения напряжения источника питания 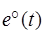, приводящий к изменению тока через сопротивление R и индуктивность L в схеме от заданного начального значения 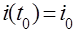до заданного конечного значения , чтобы суммарная энергия активных потерь (затрачиваемая на нагрев) при этом изменении была минимальной;

б) определить оптимальный закон изменения тока 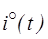, соответствующий оптимальному закону изменения ;

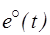в) вычислить энергию активных потерь в схеме при оптималь­ном режиме изменения напряжения и тока ( 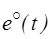, 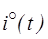) и сравнить ее с энергией активных потерь, затрачиваемой на нагрев, при линейном изменении тока в схеме от начального значения до конечного значения;

г) построить графики оптимальных и линейных изменений ЭДС и токов.

 

Описание объекта управления

 

Математическая модель объекта получается на основе законов Кирхгофа: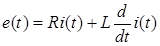

 

и имеет вид диф­ференциального уравнения

 

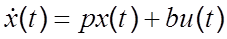, (1)

 

где x(t)=i(t) , u(t)=e(t) ,p, b – числа, равные p = – R/L, b = 1/L

 

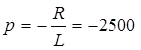
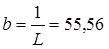
Конструирование функционала – критерия оптимальности.

Критерий оптимальности – квадратичный функционал:



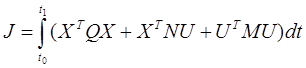
где 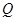- симметричная, неотрицательно-определенная матрица чисел, размерами 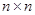; 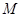- симметричная, положительно-определенная матрица чисел размерами .

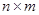В данном случае вместо матриц используются числа, поэтому критерий оптимальности будет иметь другой вид:

, (2)

Это выражение представляет собой суммарную энергию активных потерь в схеме за время (t₁–t₀)_.

 

Запишем выражение для активной мощности по­терь на сопротивлениях r и R :

, или

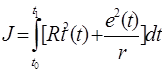
Таким образом, q = R=45, m = 1/r =1/1,5=0,67, n = 0.

 

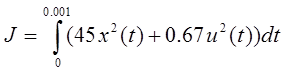
3. Формулировка задачи как вариационной задачи на услов­ный экстремум.

 

Для этого необходимо рассматривать в качестве уравнения связей уравнение системы (1), а в качестве функционала – функционал (2).

 

Таким образом, получаем следующую вариационную задачу:

 

Определить функции x(t) и u(t) доставляющие экстремум функционалу

,

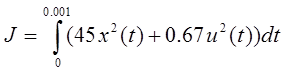при граничных условиях

,

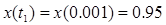
и при дополнительном условии (уравнении связи)

накладываемом на функции x(t), u(t) , в классе которых ищется экстремум.