 |
Главная |
Математическое ожидание случайной величины, его вероятностный смысл и свойства
|
из
5.00
|
В некоторых случаях закон распределения случайной величины неизвестен, или просто целесообразно использовать не таблицу или функцию распределения для представления случайной величины, а так называемые числовые характеристики ее распределения, в частности математическое ожидание.
Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:
 ,где
,где 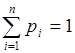 .
.
Очевидно, математическое ожидание случайной величины  не изменится, если таблицу значений этой случайной величины пополнить конечным числом любых чисел, считая, что вероятности этих чисел равны нулю.
не изменится, если таблицу значений этой случайной величины пополнить конечным числом любых чисел, считая, что вероятности этих чисел равны нулю.
Математическое ожидание  случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины
случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины  .
.
Вероятностный смысл математического ожидания: математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания можно сформулировать в виде теорем. Доказательства этих теорем будут приведены для дискретных случайных величин, однако, соответствующие теоремы справедливы также и для непрерывных случайных величин.
Прежде, чем формулировать свойства математического ожидания необходимо выяснить смысл и дать определение арифметических операций  ,
,  ,
,  и т.п., где
и т.п., где  и
и  – дискретные случайные величины.
– дискретные случайные величины.
Например, под суммой  понимается случайная величина
понимается случайная величина  , значениями которой являются все допустимые суммы
, значениями которой являются все допустимые суммы  , где
, где  и
и  – все возможные значения соответственно случайных величин
– все возможные значения соответственно случайных величин  и
и  ; причем соответствующие вероятности равны:
; причем соответствующие вероятности равны:
 .
.
Если какая-нибудь комбинация  невозможна, то условно полагают
невозможна, то условно полагают  ; это не отразится на математическом ожидании суммы. Аналогично определяются и остальные операции.
; это не отразится на математическом ожидании суммы. Аналогично определяются и остальные операции.
Свойства математического ожидания
1. Теорема. Математическое ожидание постоянной величины 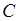 равно этой величине.
равно этой величине.
Доказательство. Постоянную величину 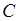 можно рассматривать как случайную дискретную величину, принимающую лишь одно возможное значение
можно рассматривать как случайную дискретную величину, принимающую лишь одно возможное значение 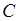 с вероятностью
с вероятностью  . Поэтому
. Поэтому  .
.
2. Теорема. Математическое ожидание суммы двух (или нескольких) случайных величин  и
и  равно разности их математических ожиданий:
равно разности их математических ожиданий:
 .
.
Доказательство:
1) Пусть случайная величина  принимает значения
принимает значения  с вероятностями
с вероятностями 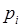 (
(  ), а случайная величина
), а случайная величина  принимает значения
принимает значения  с вероятностями
с вероятностями  (
(  ). Тогда возможными значениями случайной величины
). Тогда возможными значениями случайной величины  будут суммы
будут суммы  , вероятности которых равны:
, вероятности которых равны:

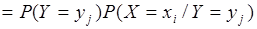 .
.
Как уже отмечалось ранее, все комбинации (  ) (
) (  ,
,  ) можно считать допустимыми, причем, если сумма
) можно считать допустимыми, причем, если сумма  невозможна, то полагаем, что
невозможна, то полагаем, что  .
.


Сумма 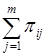 представляет собой вероятность события, состоящего в том, что случайная величина
представляет собой вероятность события, состоящего в том, что случайная величина  принимает значения
принимает значения  при условии, что случайная величина
при условии, что случайная величина  примет одно из своих возможных значений (что достоверно); это сложное событие, очевидно, эквивалентно тому, что
примет одно из своих возможных значений (что достоверно); это сложное событие, очевидно, эквивалентно тому, что  принимает значение
принимает значение  и поэтому
и поэтому  .
.
Аналогично 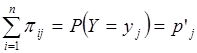 .
.
Тогда  .
.
2) Для нескольких случайных величин, например для трех  ,
,  и
и  , имеем:
, имеем:

 , и т.д.
, и т.д.
Следствие. Если 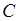 – постоянная величина, то:
– постоянная величина, то:

3. Теорема. Математическое ожидание произведения двух независимых случайных величин  и
и  равно произведению их математических ожиданий:
равно произведению их математических ожиданий:
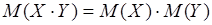 .
.
Доказательство. Пусть случайная величина принимает значения (  ,
, 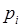 ) (
) (  ) и (
) и (  ,
,  ) (
) (  ) – законы распределения случайных величин
) – законы распределения случайных величин  и
и  . Так как
. Так как  и
и  – независимы, то полный набор значений случайной величины
– независимы, то полный набор значений случайной величины  состоит из всех произведений
состоит из всех произведений  (
(  ,
,  ), причем вероятности этих значений по теореме умножения для независимых событий равны
), причем вероятности этих значений по теореме умножения для независимых событий равны 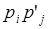

Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
Действительно, например, для трех взаимно независимых случайных величин  ,
,  и
и  :
:
 , и т.д.
, и т.д.
Следствие. Постоянный множитель можно выносить за знак математического ожидания, т.е.  . Если
. Если 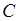 – постоянная величина и
– постоянная величина и  – любая случайная величина, то, учитывая, что
– любая случайная величина, то, учитывая, что 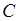 и
и  – независимы, получим:
– независимы, получим:
 .
.
Следствие. Математическое ожидание разности двух случайных величин  и
и  равно разности их математических ожиданий:
равно разности их математических ожиданий:
Доказательство. 
 .
.
|
из
5.00
|
Обсуждение в статье: Математическое ожидание случайной величины, его вероятностный смысл и свойства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

