Метод конечных разностей

Существует множество численных методов решения дифференциальных уравнений. Некоторые из них ищут решение в виде аналитических функций. Однако, для случаев со сложной геометрией или разрывами в граничных условиях такие методы становятся довольно громоздкими. Поэтому большинство численных методов решения дифференциальных уравнений рассматривают дискретно заданные («сеточные») функции, т.е. функции, заданные на некотором множестве точек, называемом сеткой.

Поговорим о сетках. В одномерном случае от сетки остается лишь конечное множество точек, заданное на отрезке, на котором ищется решение. Точки могут располагаться равномерно или неравномерно. В многомерном случае наблюдается огромное многообразие типов сеток. Приведем лишь несколько примеров. Ниже на рисунках представлены равномерные прямоугольная и треугольная сетки.

Сетки бывают неравномерными (часто линии сетки сгущают в той области, где хотят поднять точность расчета).

Сетки бывают адаптивными (например, сетка, являющаяся прямоугольной в некоторой системе координат, связанной с поверхностью).

Правильный подбор типа и параметров сетки может существенно (в отдельных случаях на порядки) сократить ресурсы, требуемые для получения результата.

Точки пересечения линий сетки называются узлами. Элементарные области, ограниченные линиями сетки (плоскостями или иными поверхностями в трехмерном случае) называются ячейками. Значения искомой функции могут задаваться либо в узлах сетки, либо в каких-либо точках (например, в центрах) ячеек.

Численные методы решения дифференциальных уравнений, работающие с сеточными функциями, сводят исходную задачу к решению системы алгебраических уравнений. Одним из самых распространенных методов является метод конечных разностей[4]. Ему будет посвящена значительная часть данного курса. Не потому, что он лучший. Просто когда-то он был самым распространенным и по нему написано огромное количество книг, в которых изложены все трудности, которые встречаются и в других методах. Например, можно почитать книжки [9, 10]. Как правило, для метода конечных разностей используют прямоугольные сетки. Значения функции рассчитываются в узлах сетки.

Аппроксимация

Итак, требуется заменить имеющиеся уравнения их дискретными аналогами. Такой процесс называется дискретизацией уравнений. Рассмотрим производные по x (производные по другим переменным записываются совершенно аналогично). Отсортируем дискретные значения переменной x по возрастанию и проиндексируем их. Значения производных в узле сетки приближенно записываются (аппроксимируются) через значения функции в данном и ближайших узлах. Обязательное условие: приближенное значение производной, посчитанное по дискретному аналогу, должно стремиться к точному значению при стремлении расстояния между узлами к нулю. Минимальное количество точек, необходимое для аппроксимации n-й производной, равно n+1. Так, первую производную можно приближенно найти, зная значение функции в 2 точках, вторую производную – в 3 точках.

Самым распространенным способом дискретизации является разложение функции в ряд Тейлора. При выводе дискретного аналога производной используются только несколько первых членов ряда (остальные полагаются равными нулю). Порядком аппроксимации называется порядок последней учитывающейся производной в ряде Тейлора[5]. Рассмотрим простейшую аппроксимацию первой производной. В точке с номером j ее можно получить двумя способами.

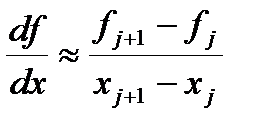
Первая из этих формул называется аппроксимацией разностью вперед, вторая – аппроксимацией разностью назад. Это формулы первого порядка. Попробуем написать формулу второго порядка.

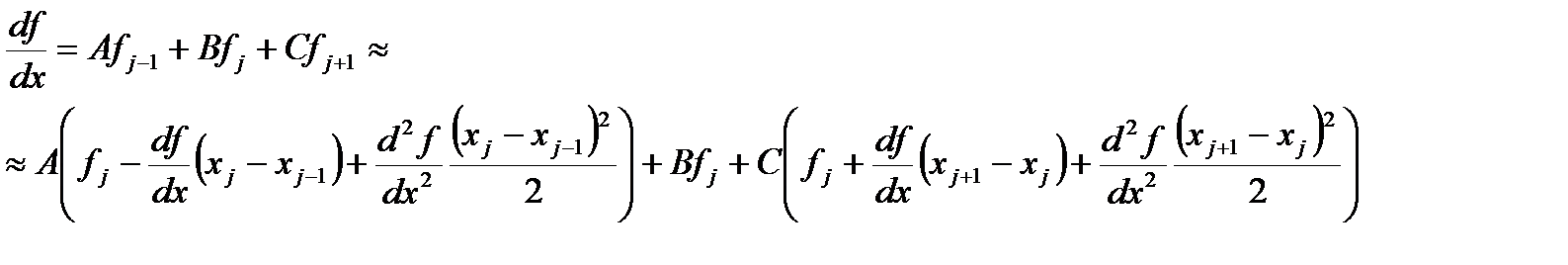
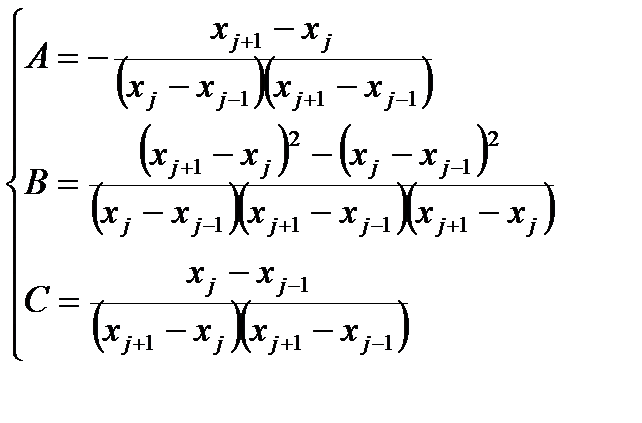
Для равномерных сеток (x_j+1-x_j)=(x_j-x_j-1). Обычно шаг сетки при этом обозначают через h. При этом запись дискретного аналога первой производной существенно упрощается

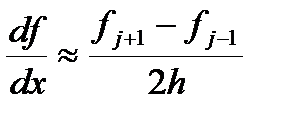
В этом случае принято говорить, что первая производная аппроксимируется центральной разностью. Аналогично записываются дискретные аналоги для второй производной.

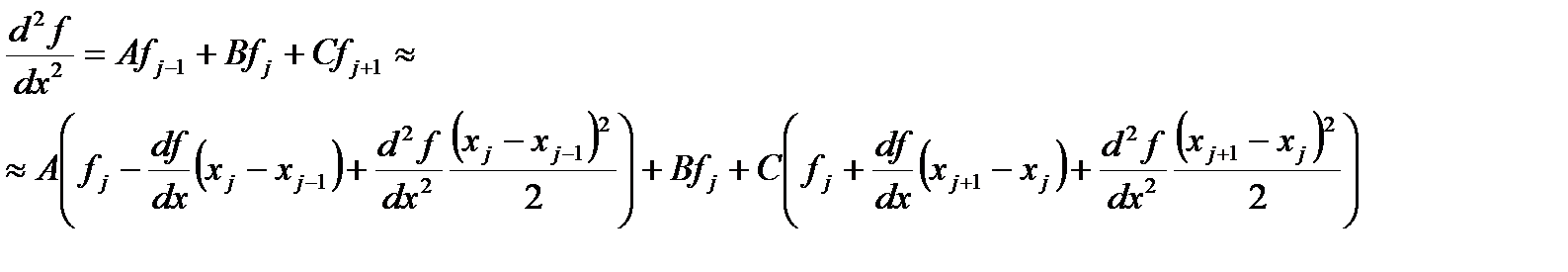
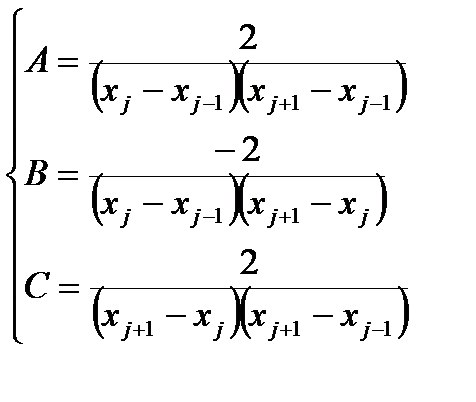
Для равномерной сетки получаем

Далее, чтобы избежать громоздких выражений, будем рассматривать только равномерные сетки.

При записи дискретного аналога дифференциальных уравнений возникает уже гораздо большее разнообразие вариантов. Рассмотрим волновое дифференциальное уравнение первого порядка.

Оно описывает распространение волны (перенос массы или заряда) со скоростью a. Как указывалось выше к таким уравнениям можно свести гиперболические уравнения. Будем рассматривать именно такой случай. Считаем, что мы идем маршевым методом по времени. Нам известно распределение функции по x в некоторый момент времени и нужно найти распределение в следующий момент. Рассмотрим аппроксимации первого порядка. Значения функции в узлах сетки будем обозначать f_,jk, где первый индекс относится к значению времени, а второй – координаты. Производную по времени аппроксимируем выражением

где t - шаг по времени. А производную по координате можно аппроксимировать как разностями вперед, так и разностями назад. Получаем первые две возможные аппроксимации.

Для наглядности часто рисуют графические изображения разностных схем, называемые шаблонами. Приведем шаблоны двух описанных формул. На рисунках считается, что координата x идет горизонтально слева направо, а ось y направлена вертикально снизу вверх.

Строгих стандартов на шаблоны не существует. Например, часто рисуют стрелки из узлов, где значения известны, в узел (узлы), где значения неизвестны. Часто в одной книге шаблоны нарисованы в разных местах в разных стилях. Здесь, тоже не будем придерживаться одного стиля.

За приведенные графические изображения рассмотренные схемы часто называют «правый уголок» и «левый уголок». В обеих этих схемах на новом (по времени) слое используется лишь один узел, следовательно, значение в этом узле можно явным образом выразить через значения в других узлах.

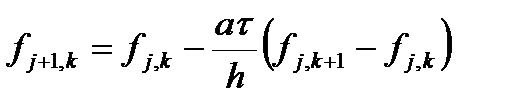
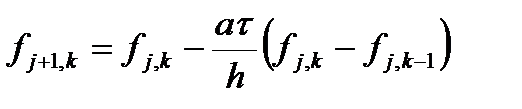
Такие схемы называются явными. Зная значения на j-м слое, легко получаются значения на j+1-м слое. Если производную по координате выписать на новом слое, то получим две неявные схемы.

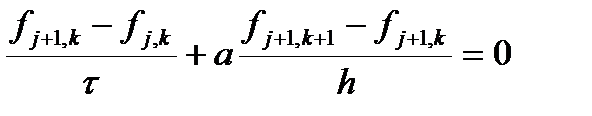
Они имеют следующие шаблоны

 

В случае неявной схемы мы получаем не конечную формулу для значения функции в узле, а связи между неизвестными значениями в узлах на новом слое. Перебрав все значения индекса k мы получаем систему (линейных) алгебраических уравнений, которую надо решить для получения искомых значений. В рассматриваемом случае можно отделаться малой кровью. Каждое уравнение будет связывать два соседних узла. Найдя значение в каком-либо узле на новом слое, легко получить значение в соседнем. Далее, двигаясь по цепочке, получаем значения во всех узлах на новом слое. Таким образом, нужно знать хотя бы одно значение. Его можно взять из граничного условия. В общем случае в неявных схемах без специальных ухищрений не удается обойтись без решения системы уравнений.

Посмотрим, что мы реально считаем методом конечных разностей. Выберем схему «правый уголок». Разложим искомую функцию в ряд Тейлора в окрестности точки с индаксами j и k и учтем члены со второй производной. Итак, имеем

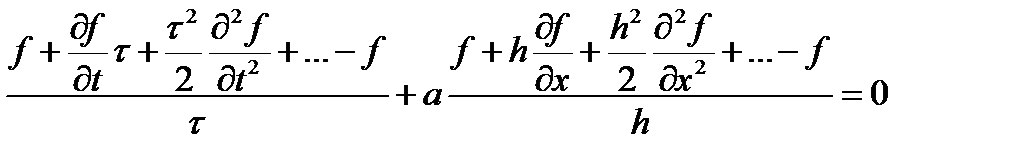
после сокращения получаем, то, что решаем реально

То есть, дискретизация привела к тому, что, надеясь решить одно уравнение, получаем решение другого уравнения. Радует лишь то, что с уменьшением шагов по времени и по пространству разница между уравнениями уменьшается. Тем не менее, при любых ненулевых шагах реально решаемое уравнение может не только иметь иные (по сравнению с исходным) свойства, но даже принадлежать к другому типу. Например, исходное рассматриваемое уравнение предполагает, что волна движется в пространстве не меняя своей формы. Для демонстрации зададим в качестве начального распределения разрывное распределение (см. случай а на рисунке ниже). Если неудачно выбрана расчетная схема или ее параметры, то можно получить решения, показанные на том же рисунке с обозначениями б и в, или вообще не получить никакого разумного решения.

 

а б в

 

Теперь рассмотрим параболическое уравнение, а именно цветовое уравнение

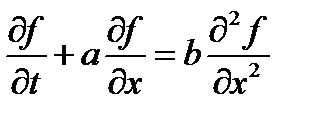
(Как отмечалось выше, такое название оно получило за то, что описывает, в том числе, распространение подкрашенной жидкости в воде.) Параметр a определяет скорость конвективного переноса концентрации (или, например, температуры), а параметр b определяет диффузию (теплопередачу). Выберем явную схему. Первую производную по пространству для начала аппроксимируем с помощью правой разности. Получаем дискретный аналог дифференциального уравнения

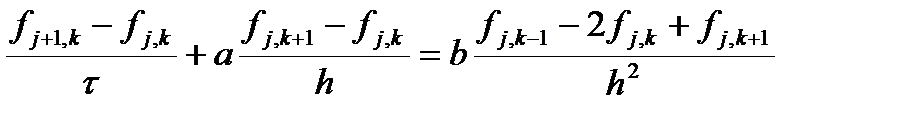
Как и раньше разложим функцию в ряд Тейлора, но по пространству учтем третью производную.

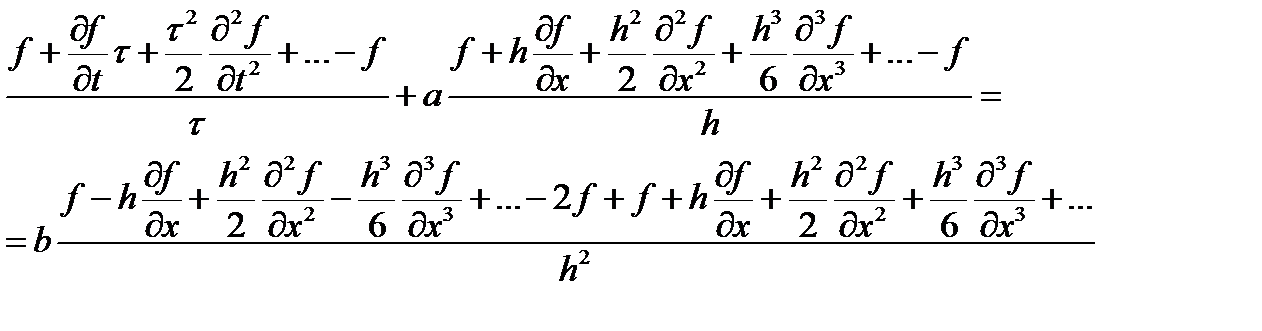
после сокращений получаем

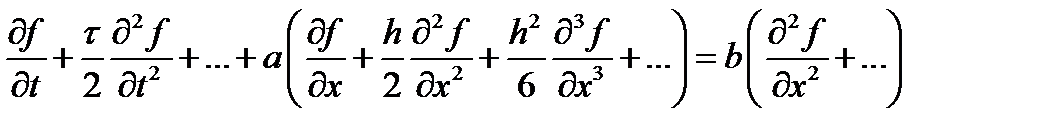
теперь сгруппируем вторые производные по x. Получим

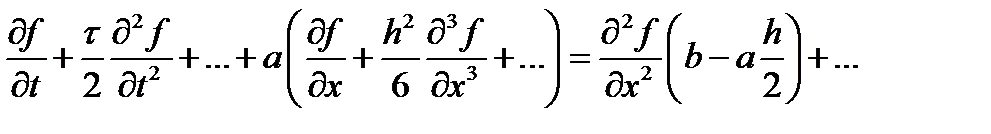
То есть получается, что мы не только решаем другое уравнение, но и коэффициенты в нем другие. Коэффициент b имеет физический смысл коэффициента диффузии (теплопроводности, вязкости) и не может быть отрицательным. А у нас получилось, что при 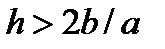коэффициент диффузии становится отрицательным, что не соответствует никакой физике. Добавку к коэффициенту диффузии (теплопроводности, вязкости) принято называть сеточной (или схемной) диффузией (теплопроводностью, вязкостью).

Теперь рассмотрим случай, когда первая производная аппроксимируется центральной разностью. Получаем дискретный аналог дифференциального уравнения

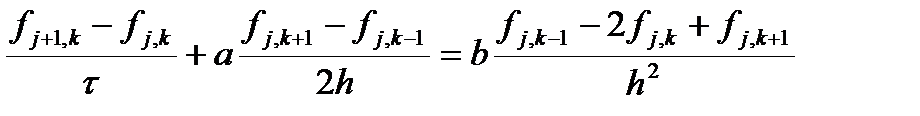
Как и раньше разложим функцию в ряд Тейлора, но по пространству учтем третью производную.

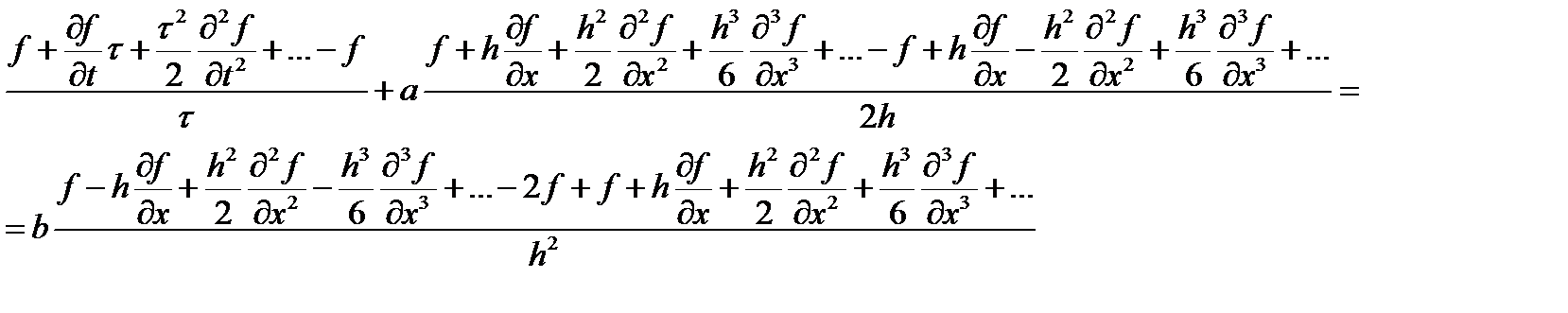
после сокращений получаем

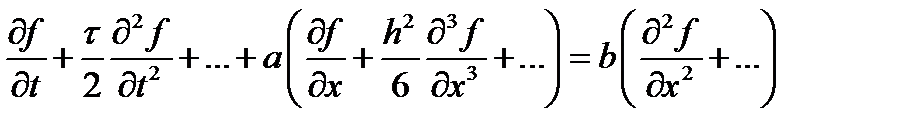
По сравнению с исходным уравнением присутствуют член, пропорциональный первой степени шага по времени, и член, пропорциональный второй степени шага по пространству. В таком случае говорят, что данная схема имеет второй порядок аппроксимации по простронству и первый – по времени. В целом, когда говорят о порядке аппроксимации уравнения, под порядком понимают наименьший из порядков аппроксимации по всем переменным. В данном случае мы имеем аппроксимацию первого порядка.

Для линейных уравнений есть «точные» оценки погрешности расчета. Но при моделировании плазмы, как правило, приходится иметь дело с нелинейными уравнениями. Для них точных оценок нет. Для оценки точности расчета обычно проводят два (иногда больше) расчета на разных сетках. Если на второй сетке шаги по всем переменным вдвое меньше, чем на первой, и схема имеет первый порядок аппроксимации, то погрешность уменьшится примерно вдвое. «Примерно» потому, что в разложении в ряд Тейлора существуют члены с производными более высоких порядков и, соответственно, с более высокими степенями шагов. Таким образом, разница между результатами расчетов будет примерно соответствовать погрешности расчета с более мелкой сеткой. Если использовалась аппроксимация второго порядка, то уменьшение шагов вдвое приводит к уменьшению погрешности примерно в четыре раза.

Следует отметить, что для таких оценок необходимо пропорционально изменять и шаг по времени и шаг по пространству. Если уменьшать только один из шагов, оставляя другой без изменения, то погрешность может как увеличиваться, так и возрастать. Объясняется это тем, что погрешность зависит и от соотношения шагов. Для того, чтобы это наглядно показать, составим дифференциальное приближение волнового уравнения первого порядка. От проделанных выше операций эта процедура отличается исключением высших производных по времени из реально решаемых уравнений. Итак, рассматриваем уравнение

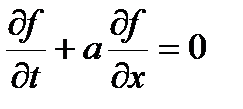
используя следующую разностную схему

.

Для этого случая мы ранее уже получили выражение

.

Чтобы выразить вторую производную по времени через производные по пространству продифференцируем исходное уравнение по времени. Получаем

.

Выразим первую производную по времени через исходное уравнение

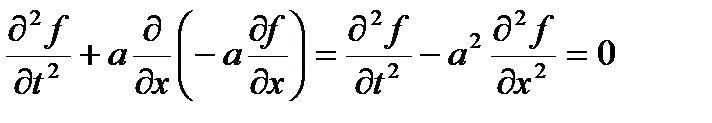
Теперь реально решаемое уравнение можно записать в виде

.

Полученный результат называется дифференциальным приближением рассматриваемой разностной схемы. Из него видно, что наименьшую погрешность можно получить, задав шаги, связанные соотношением

h=aτ.

Как показано выше, члены, отвечающие за погрешность в реально решаемых уравнениях, пропорциональны некоторым производным от искомой функции. Но в природе, в том числе и в плазме, могут существовать области с очень большими градиентами. Часто проще их описать разрывными функциями. Значения производных в этих областях очень велики (для разрывов – бесконечны), следовательно, и погрешность численного решения может быть недопустимо большой. Простого универсального метода обхода этой неприятности для произвольной системы дифференциальных уравнений нет. Но для уравнений магнито-гидродинамики такой способ есть. Рассмотрим две эквивалентные записи уравнения, описывающего перенос массы (или заряда) вдоль оси

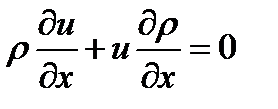
Будем считать, что распределение плотности вдоль оси нам известно. Причем плотность задана разрывной функцией

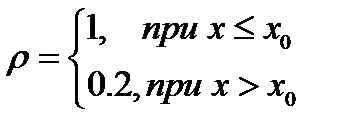
Пусть x₀>0, u(0)=1. Очевидно, что аналитическое решение для скорости будет

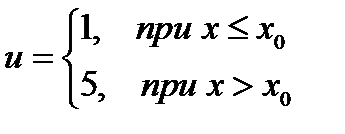
Попробуем решить уравнение во второй форме записи методом конечных разностей. Распишем разностную схему

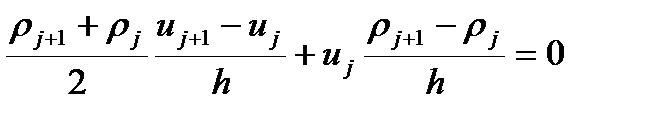
Выразим значение скорости в следующей точке через значение в предыдущей

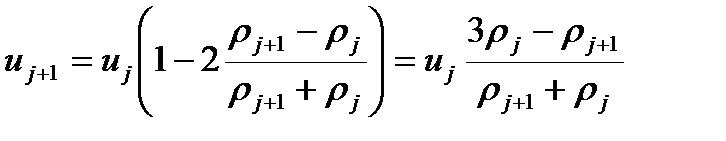
Получаем, что при переходе через разрыв скорость получит новое значение 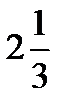. То есть расход массы (заряда) снизился примерно вдвое. Причем этот результат не зависит от шага сетки. Если мы используем первую форму записи уравнения, то схема записывается

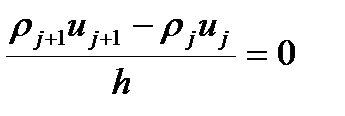
скорость в следующей точке равна

При переходе через разрыв получаем точное решение. Чтобы избежать подобных проблем исходные уравнения, по возможности, нужно приводить к виду

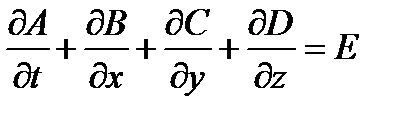
То есть без коэффициентов перед производными. Такой вид называется дивиргентным. Иногда говорят о дивиргентной форме записи уравнения. Если в уравнениях магнто-гидродинамики не учитываются вязкость, диффузия и теплопроводность (т.е. процессы, при записи которых используются вторые производные), то их можно привести к дивиргентному виду. Рассмотрим правые части уравнения сохранения массы и одного из уравнений сохранения импульса

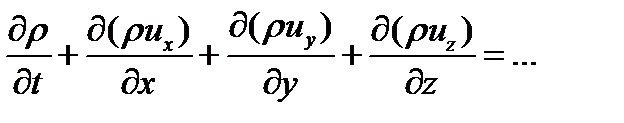
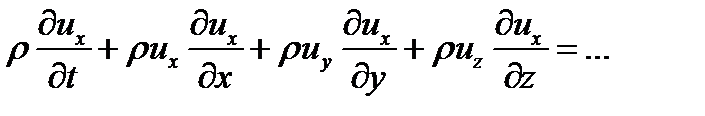
первое из них уже в дивиргентной форме. А второе можно привести к дивиргентному виду если прибавить к нему первое уравнение умноженное на u_x. Тогда получаем

Окончательно уравнение импульса переписывается в виде

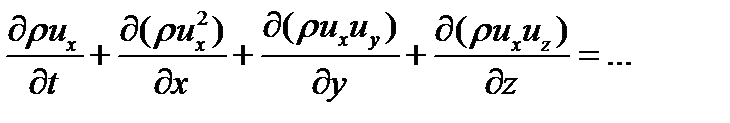
Устойчивость

Итак, будем считать, что аппроксимировать дифференциальные уравнения дискретными аналогами мы научились. Но выясняется, что не каждая разностная схема, полученная в полном соответствии с теорией аппроксимации, позволяет получить разумный результат. Дело в том, что как бы точно ни были заданы начальное приближение, начальные и граничные условия, всегда найдется какая-нибудь погрешность. Как минимум будут ошибки округления. При некоторых условиях эти ошибки начинают быстро расти. В конце концов, это может привести к тому, что результат опять не будет ничего общего иметь с моделируемым процессом.

Условие, что погрешности не накапливаются, называется условием устойчивости. Существует много методов проверки различных численных схем на устойчивость. Рассмотрим два из них.

Первый способ не очень точен, применение его бывает довольно громоздким, но он интуитивно понятен и надежен. Называется методом дискретного возмущения[6]. В методе предполагается, что во всех узлах решение точное, кроме одного, в котором возмущение равно d. Далее следят за развитием этого возмущения и пытаются выяснить, при каких условиях оно нарастает.

Начнем с простого уравнения первого порядка. Рассмотрим решение волнового уравнения схемой «уголок». Итак, имеем разностную схему

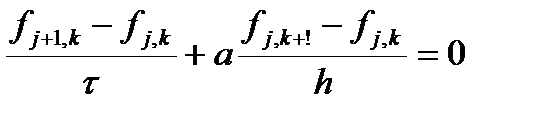
откуда выражаем значение на новом слое

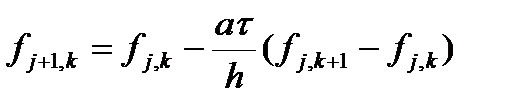
Безразмерный комплекс 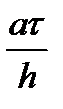называется числом Куранта и обычно обозначается C. Теперь выражение для значения на следующем слое можно записать более кратко

f_j+1,k=(1+C)f_j,k-Cf_j,k+1

В силу линейности уравнения возмущения будут описываться таким же соотношением. Для доказательства представим значение в каждой точке в виде суммы точного решения реально решаемого уравнения (будем обозначать его звездочкой) и погрешности.

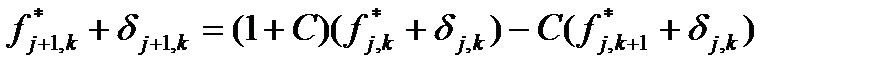
Вычитая из данного соотношения уравнение для точного решения получаем

δ_j+1,k=(1+C)δ_j,k-Cδ_j,k+1

Считаем, что на j-м слое все возмущения, кроме k-го, равны нулю. Возмущение в k-й точке равно d. Тогда на j+1-м слое будут два ненулевых возмущения:

d_j+1,k-1=-Cd

d_j+1,k=(1+C)d

Чтобы схема была устойчивой, требуется, чтобы максимальное по модулю возмущение на новом слое было меньше или равно максимальному по модулю возмущению на предыдущем слое. Из соотношения для k-1-го узла получаем: |C|£1. Из соотношения для k-го узла имеем: -2£C£0. Следовательно: -1£C£0. Теперь рассмотрим k+2-й слой. Там будут три ненулевых возмущения:

d_j+2,k-2=-C²d

d_j+2,k-1=-2C(1+С)d

d_j+1,k=(1+C)²d

Их надо сравнить с максимальным по модулю возмущением из j+1-м. Желающие могут убедиться, что новых ограничений мы не получим. Не получим их и если рассмотреть последующие слои. Окончательно имеем: ‑1£C£0. Так как шаги по времени и по пространству положительны, то получаем, что использовать такую схему можно только при a£0. Причем шаг по времени должен удовлетворять соотношению

Все это было проделано для схемы, где производная по пространству аппроксимировалась разностью вперед. Все тоже самое можно проделать для схемы с разностью назад. Желающие могут проделать такие же выкладки. Я здесь привожу конечный результат: 0£C£1. То есть «левый уголок» для этого уравнения можно применять только при положительных a.

Применение метода дискретного возмущения для неявных схем затруднительно.

Условие |C|£1 называется условием Куранта-Фридрихса-Леви. Вообще говоря, это условие является необходимым (но не достаточным!) для всех явных схем для дифференциальных уравнений гиперболического типа.

У полученных результатов (в том числе и у условия Куранта-Фридрихса-Леви) есть несколько трактовок и интерпретаций. Рассмотрим сначала интерпретацию с помощью характеристик. Здесь полезно графическое изображение. Сначала мы рассматривали «правый уголок». Проведем характеристику через точку на новом слое. Рассмотрим неустойчивые случаи: a>0 и |C|>1. Характеристика показана на рисунке красным цветом

А теперь посмотрим, как выглядит картинка для устойчивого случая

 

Из рисунков очевидно следует простая интерпретация: характеристика, приходящая в точку, где мы хотим найти значение, должна пересекать отрезок, соединяющий какие-либо две другие точки в используемом шаблоне. Как отмечалось выше, характеристика идущая в точку, где нужно найти значение, должна приходить из области, где значение известно. В данном случае, такой областью является отрезок, соединяющий две точки, используемые в шаблоне (на отрезке всегда можно найти значение с помощью интерполяции).

Еще одна интерпретация условия Куранта-Фридрихса-Леви гласит: численное возмущение должно распространяться по сетке не медленнее, чем распространяется в пространстве возмущение в моделируемом процессе. Так, в рассмотренном примере возмущение, заданное в одной точке на слое, на следующем слое было уже и в соседней точке. То есть за время t оно распространилось в пространстве на расстояние h. Таким образом, скорость распространения численного возмущения составила 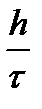. Для устойчивости эта скорость должна быть больше или равна физической скорости a. Нетрудно заметить, что это и утверждается условием Куранта-Фридрихса-Леви.

При использовании схемы «левый уголок» картинки симметричны рассмотренным. Отсюда следует простое правило: при использовании схемы типа «уголок» нужно использовать разность навстречу потоку (против потока).

Самым популярным методом исследования разностных схем на устойчивость является спектральный признак устойчивости (он же метод фон Неймана). Он точен для линейных уравнений с постоянными коэффициентами. Итак, будем искать ошибку в виде

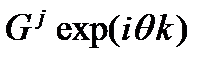
это соответствует представлению функции ошибки в виде интеграла Фурье. При этом G отвечает за амплитуду колебаний, а q - за период колебаний. Требование устойчивости сводится к условию

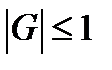
при любых значениях q. Рассмотрим применение этого метода к неявным схемам типа «уголок» для волнового уравнения первой степени. Возьмем разностную схему вида

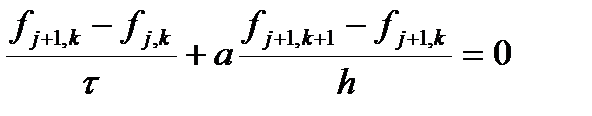
подставляем выражение для ошибки

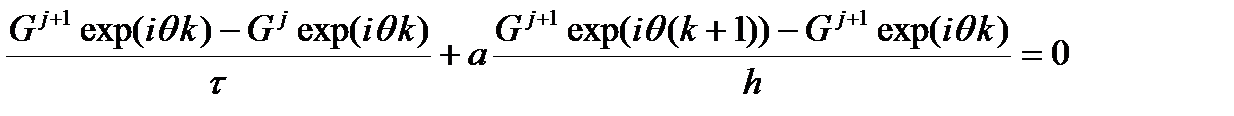
сокращая на G^jexp(iθk) получаем

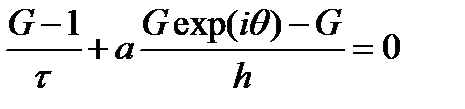
преобразуем выражение

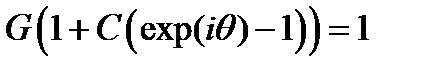
из условия устойчивости получаем

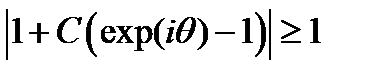
Построим на комплексной плоскости возможные значения левой части полученного выражения. Геометрическое точек представляет собой окружность единичного радиуса с центром в точке -1. Выражение, стоящее под модулем, описывает окружность радиусом C с центром в точке 1-C. Таким образом, получаем следующее графическое представление

С=-1

С=0.5

С=1

С=2

Отсюда наглядно видно, что при С=1 получаем единичную окружность, т.е. неравенство превращается в равенство. Это означает, что величина ошибки будет оставаться на прежнем уровне (не будет расти, но и не будет уменьшаться). Неравенство выполняется при С£0 и при С³1. При 0<C<1 схема неустойчива.

Дадим другую графическую интерпретацию полученного результата. Проведем характеристику через одну из точек на новом слое. Получаем

C<0 0<C<1 C>1

 

Совершенно аналогично можно рассмотреть другую неявную схему

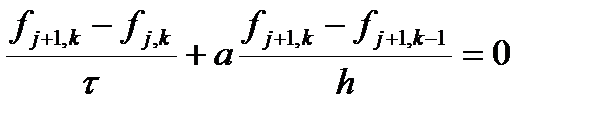
Естественно, получим устойчивость при С£-1 и при С³0. При -1<C<0 схема неустойчива. Видно, что обеспечить устойчивость неявных схем гораздо проще. Так, если использовать схемы с разностью против потока, то такие схемы будут устойчивы при любом модуле числа Куранта. Такие свойства неявных схем обеспечили им широкое применение.

Рассмотрим теперь устойчивость разностных схем для параболических уравнений. В них возмущения распространяются с бесконечно большой скоростью. В принятой в данной писанине графической интерпретации характеристики параболических уравнений вырождаются в горизонтальные линии. Может показаться, что из этого следует неустойчивость всех явных разностных схем для параболических уравнений. Но, как отмечалось выше, разностные схемы описывают не исходные уравнения, а некоторые другие. Эти другие уравнения могут иметь совершенно иные свойства. Обычно этот факт приносит сплошные неприятности. Но нет худа без добра. Реально решаемые уравнения могут оказаться не параболическими а гиперболическими, а для таких явные схемы могут быть устойчивыми.

Ранее рассматривалась явная разностная схема для цветового уравнения

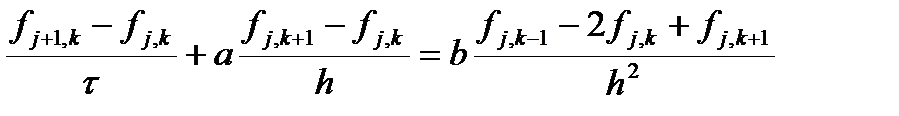
Применим метод фон Неймана для анализа ее устойчивости.

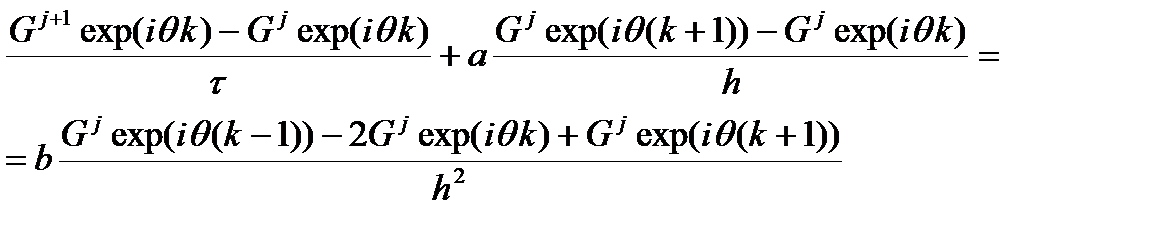
Проведем ряд сокращений

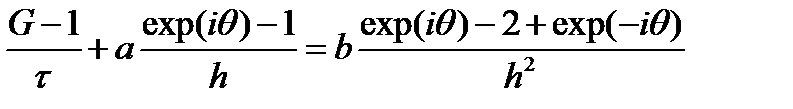
комплекс 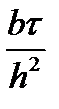не имеет общепринятого названия, для краткости будем обозначать его через D. Воспользуемся также формулой Эйлера

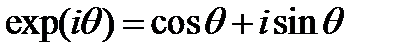
Тогда имеем

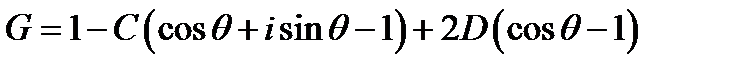
Геометрическое место таких точек на комплексной плоскости будет представлять собой эллипс с центром в точке 1+C-2D. Полуось в направлении оси X равна |2D-C|, а полуось в направлении оси Y равна С. В соответствии с условием устойчивости этот эллипс не должен выходить за пределы единичной окружности. Из рассмотрения пересечения эллипса с осями координат следует: |C|£1 и -1£C-2D£0. Еще одно ограничение возникает из рассмотрения радиуса кривизны эллипса в точке касания с единичной окружностью: С²£|2D-C|. Все четыре возможных варианта эллипсов, соответствующих неустойчивым схемам представлены на рисунке (единичная окружность показана красным цветом).

6 b4W77YMUz9d3KiO3W2BS+e8HvYgOd/9j3Knyp8CdI20fKt3H6rutE2+b8wI71ZYhnoLC9C827k3/ dmh7D7SBnRW/ChAWF35OkAciE1z93gJ/JLH9XfTa/Crk5D8AAAD//wMAUEsDBBQABgAIAAAAIQBr gL9H3QAAAAUBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI9BS8QwEIXvgv8hjODNTSy73VqbLiIoogd1 LXjNNrNtMJmUJrut/nqjF70MPN7jvW+qzewsO+IYjCcJlwsBDKn12lAnoXm7uyiAhahIK+sJJXxi gE19elKpUvuJXvG4jR1LJRRKJaGPcSg5D22PToWFH5CSt/ejUzHJseN6VFMqd5ZnQuTcKUNpoVcD 3vbYfmwPTsIy29vi5T5/+npomunxfWnW4tlIeX4231wDizjHvzD84Cd0qBPTzh9IB2YlpEfi701e kV3lwHYSVmK1Bl5X/D99/Q0AAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAA AAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQB AAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQC0jCDORgYAAF0y AAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQBrgL9H3QAA AAUBAAAPAAAAAAAAAAAAAAAAAKAIAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAqgkA AAAA ">

|C|>1

C-2D<-1

C-2D>0

С2>|2D-C|

Проанализировав эти ограничения, можно оставить только два из них (остальные выполнятся автоматически): 2D£C+1 и C²+C£2D. К ним можно добавить, что для уравнений, описывающих реальные процессы в плазме величина D всегда положительна, т.к. положительны все величины, входящие в ее определение.

Теперь рассмотрим эти ограничения с точки зрения шагов по пространству и времени. Перепишем второе ограничение в виде

разделив полученное равенство на шаг по времени и умножив на квадрат шага по пространству получаем:

После несложного преобразования получаем

Ранее было показано, что то, что стоит в левой части полученного неравенства, является коэффициентом вязкости (теплопроводности, диффузии) в реально решаемом уравнении. В правой части неравенства стоит заведомо неотрицательная величина. Таким образом, это условие устойчивости можно сформулировать так: в реально решаемом уравнении (еще точнее: в дифференциальном приближении) коэффициент вязкости (теплопроводности, диффузии) должен быть неотрицательным[7]. Это же неравенство можно рассматривать как ограничение на шаг по пространству. Таким образом, при численном решении параболических уравнений с использованием явных схем существуют не только ограничения на шаг по времени, но и ограничения на шаги по пространству.

Такое ограничение на шаг можно снять, если для аппроксимации первой производной по пространству использовать центральную разность. Ранее было показано, что коэффициент вязкости (теплопроводности, диффузии) при этом не меняется в зависимости от шага. Проверяем. Запишем разностную схему

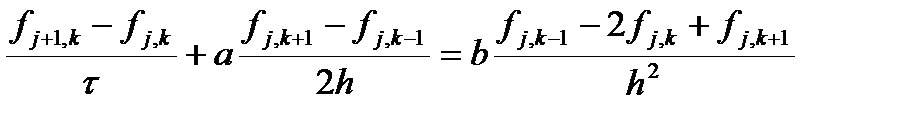
Применим метод фон Неймана для анализа ее устойчивости.

Проведем ряд сокращений

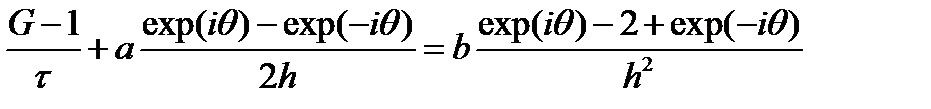
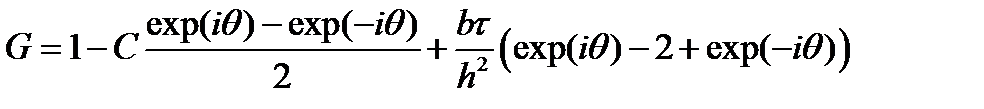
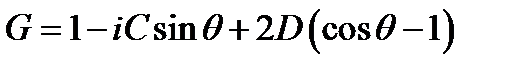
Геометрическое место таких точек на комплексной плоскости будет представлять собой эллипс с центром в точке 1-2D. Полуось в направлении оси X равна 2D, а полуось в направлении оси Y равна С. В соответствии с условием устойчивости этот эллипс не должен выходить за пределы единичной окружности. Из рассмотрения пересечения эллипса с осями координат следует: |C|£1 и 0£D£0.5. Еще одно ограничение возникает из рассмотрения радиуса кривизны эллипса в точке касания с единичной окружностью: С²£2D. Подставив в последнее неравенство вместо безразмерных чисел их определения, получаем

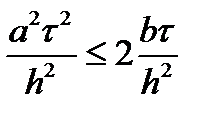
откуда

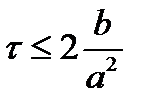
Теперь рассмотрим ограничение на величину D

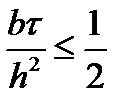
откуда

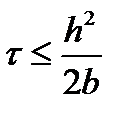
Таким образом, ограничение на шаг по пространству снято, зато появились два новых ограничения на шаг времени. Следует отметить, что одно из этих ограничений не зависит от шага по пространству и определяется только физическими величинами.

Давненько в этом тексте не упоминались эллиптические уравнения. Ранее писалось, что для их решения вводят новую переменную и сводят задачу к решению параболического уравнения. Рассмотрим, как это происходит, на примере уравнения Лапласа.

Превращаем его в параболическое уравнение

Напишем разностную схему

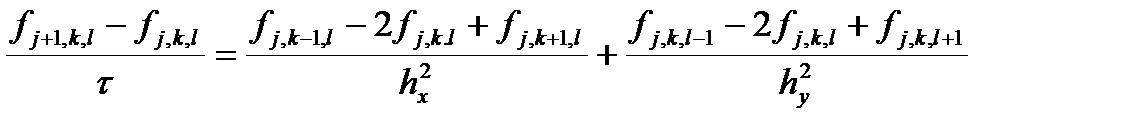
Применим метод фон Неймана (теперь в нем будут фигурировать две экспоненты и две переменные, отвечающие за периоды колебаний)

сокращая получаем

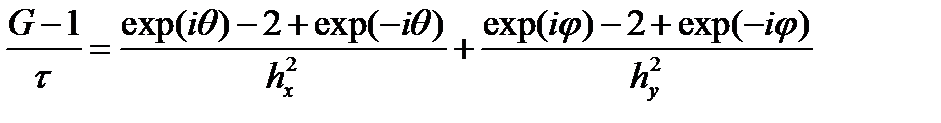
Применяя формулу Эйлера получаем

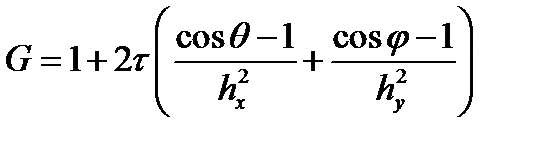
Схема будет устойчивой, если модуль G будет меньше единицы при любых значениях q и j. Отсюда легко получаем

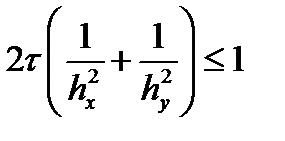
или

Если шаги по обоим пространственным направлениям равны, то формула упрощается

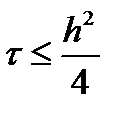
Теперь рассмотрим, что станет с рассмотренной разностной схемой, если в нее подставить максимальное допустимое значение шага по времени.

Перенесем все члены из левой части в правую. Получим

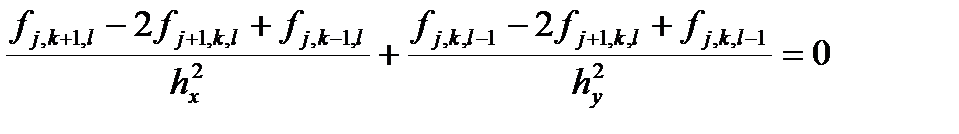
Как видно, такое уравнение соответствует разностному аналогу исходного уравнения (до введения дополнительной переменной) у которого значение центрального элемента взято на новом слое. Новая переменная уже не присутствует в разностной схеме, поэтому обычно говорят не о слоях по времени, а об итерациях.

Выразим явным образом значение функции на новой итерации

В случае если шаги по разным направлениям равны, то формула становится еще проще

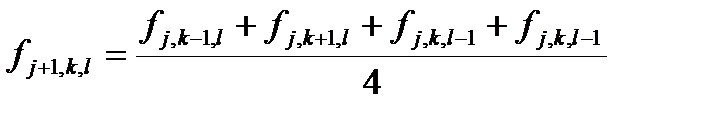
т.е. в этом случае новое значение функции в узле равно среднему арифметическому значений в соседних узлах.

До сих пор мы рассматривали отдельные уравнения. Теперь надо упомянуть системы уравнений. Рассмотрим простейшую систему дифференциальных уравнений.

Используем явную схему типа «уголок»

Воспользуемся спектральным методом для анализа устойчивости. Запишем в матричной форме.

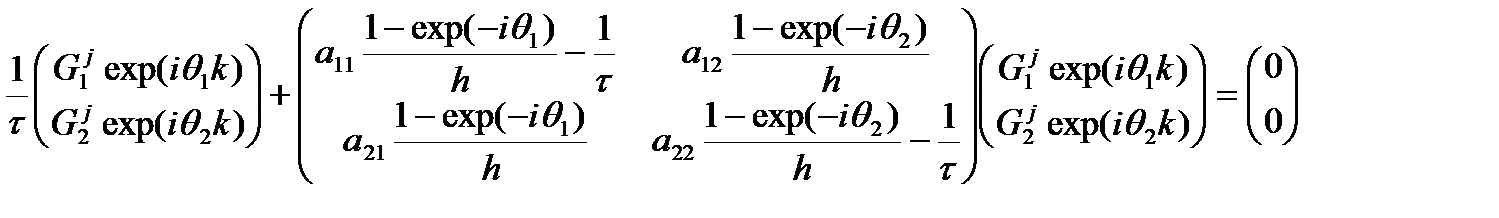
Умножим на шаг по времени и перенесем первый вектор-столбец в правую часть

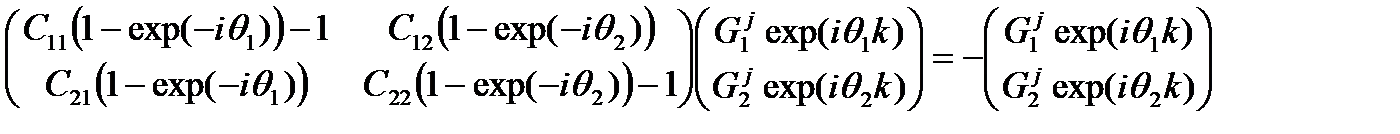
Вектор-столбцы представляют собой погрешности на текущем и следующем шагах по времени. Линейная алгебра учит, что существуют такие числа l, что погрешность на новом слое будет ровно в l раз больше погрешности на текущем. Критерием устойчивости при этом гласит: максимальный модуль l не должен превосходить 1. Согласно той же самой алгебре для нахождения таких чисел приравниваем нулю определитель матрицы

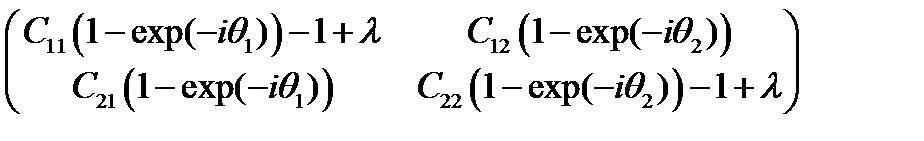
получаем квадратное уравнение

Это уравнение, конечно, можно решить аналитически, после чего тщательно исследовать условия устойчивости. Но в случае, когда имеется несколько нелинейных уравнений (типичная ситуация при расчетах плазмы), задача может стать нерешаемой в принципе.

Следует вспомнить, что метод фон Неймана точен для линейных уравнений с постоянными коэффициентами. К тому же, все что до сих пор рассм