Методы взвешенных невязок

Изучив один метод относительно подробно, переходим к изложению прочих методов целыми классами. Самым распространенным классом являются методы взвешенных невязок. Они исходят из предположения, что искомую функцию можно представить в виде функционального ряда, например такого:

Функцию f₀ обычно стараются выбирать так, чтобы она максимально точно (по возможности) удовлетворяла начальным и граничным условиям. Аппроксимирующие (пробные) функции f_j предполагаются известными. Математики напридумывали некоторое количество требований к таким функциям, но их здесь обсуждать не будем. Ограничимся фактом, что полиномы и тригонометрические функции этим требованиям удовлетворяют. Еще несколько примеров наборов подобных функций будут рассмотрены при описании конкретных методов.

Коэффициенты a_j заранее неизвестны, и их следует определять из системы уравнений, получаемой из исходного уравнения. От бесконечного ряда берут лишь некоторое конечное число членов.

В уравнении, которое предполагается решить, все члены переписываются в левую часть, в правой части остается лишь нуль. Таким образом, уравнение приводится к виду

Если приближенное решение (записанное в виде конечной суммы заранее выбранных функций) подставить в это уравнение, то оно не будет тождественно удовлетворяться. Следовательно, можно записать

где величина R называется невязкой. В общем случае невязка является функцией x, y, z и t. Задача сводится к нахождению таких коэффициентов a_j, чтобы невязка оставалась малой во всей расчетной области. Под понятием «малой» в данных методах понимают, что интегралы по расчетной области от невязки, умноженной на некоторые весовые функции, равны нулю. То есть

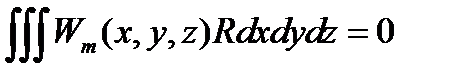
Задав конечное число весовых функций, получаем систему уравнений для нахождения неизвестных коэффициентов. Задавая различные пробные аппроксимирующие (пробные) и различные весовые функции, легко получаем целый класс методов, называемый методами взвешенных невязок.

Приведем несколько примеров простейших методов из этого класса.

Метод подобластей. Расчетная область разделяется на несколько подобластей D_m, могущих перекрывать друг друга. Весовую функцию задают в виде

Таким образом, обеспечивается равенство нулю интеграла от невязки по каждой подобласти. Метод послужил основой для ряда методов (один из них будет рассмотрена ниже).

Метод колокаций. В качестве весовых функций используются дельта-функция Дирака

где x=(x,y,z). Напоминаю, что функция Дирака – это хитрая функция[8], равная нулю везде, кроме начала координат. Но в начале она принимает неизвестное науке значение такое, что любой интеграл по области, содержащей начало координат, равен единице. Говоря проще: задаем некоторое количество точек (часто в данном подходе называемых узлами). Исходное уравнение будет удовлетворяться в этих точках. Существуют подходы к выбору этих точек и пробных функций, позволяющие максимизировать точность при ограниченном числе узлов. Но здесь их обсуждать не будем.

Метод наименьших квадратов. Метод основан на минимизации величины

Но нетрудно показать, что он тоже принадлежит к классу методов взвешенных невязок. Весовыми функциями для него являются функции вида

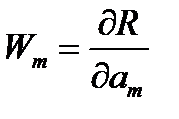
Пожалуй, это самый известный среди неспециалистов метод из данного класса, но далеко не самый популярный у специалистов.

Метод Галеркина. В этом методе в качестве весовых функций берутся аппроксимирующие (пробные) функции. То есть

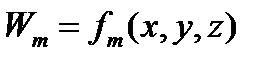
Метод широко используется в случаях, когда хотят найти решение в виде непрерывной (а не сеточной) функции.

Рассмотрим применение этих методов к расчету деформации консольно закрепленной балки длиной L. Пусть отклонение от осевой линии описывается уравнением

Граничные условия заданы в виде

f(0)=0

f'(0)=0

Будем искать решение в виде

f(x)=ax²+bx³

Тогда невязка будет записываться в виде

Для нахождения неизвестных коэффициентов a и b нам потребуется составить систему из двух уравнений. Проделаем это всеми рассмотренными методами.

Метод колокаций. Выбираем две точки на концах балки. Приравниваем в них невязку к нулю

Получаем

Как видим, метод колокаций достаточно прост в реализации, однако уступает по точности остальным методам.

Метод подобластей. Разбиваем всю длину балки на две подобласти. В каждой из них интеграл от невязки приравниваем к нулю.

Метод Галеркина. Берем интегралы от невязки, умноженной на пробные функции.

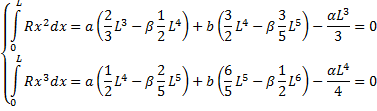
Метод наименьших квадратов.

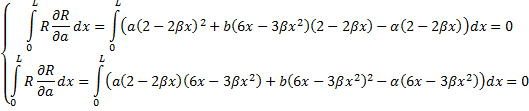
Метод наименьших квадратов требует наибольших вычислительных затрат, не давая при этом заметного выигрыша в точности. Поэтому он редко применяется в решении практических задач.