Метод левых прямоугольников и метод правых прямоугольников

Перейдем к модификациям метода прямоугольников.

- это формула метода левых прямоугольников.

- это формула метода правых прямоугольников.

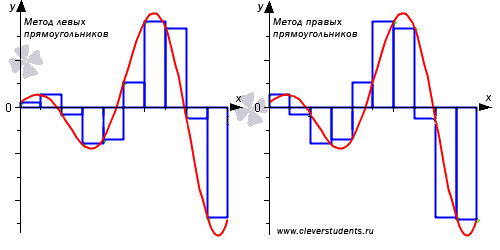
Отличие от метода средних прямоугольников заключается в выборе точек не в середине, а на левой и правой границах элементарных отрезков соответственно.

Абсолютная погрешность методов левых и правых прямоугольников оценивается как .

 

 

Pascal

234567891011121314151617

Program pravii; {Метод правых прямоугольников}uses crt;var i,n:integer; a,b,h,x,xb,s:real;function f(x:real):real;begin f:=(1/x)*sin(3.14*x/2); end;beginclrscr;write('Введите нижний предел интегрирования '); readln(a);write('Введите верхний предел интегрирования '); readln(b);write('Введите количество отрезков '); readln(n);h:=(b-a)/n; s:=0; xb:=a;for i:=1 to n dobegin x:=xb+i*h; s:=s+f(x)*h; end; writeln('Интеграл равен ',s:12:10); readln;

Блок-Схема

 

 

Excel

 

Для того, чтобы вычислить интеграл по формуле правых прямоугольников в Excel, необходимо выполнить следующие действия:

1. Продолжить работу в том же документе, что и при вычислении интеграла по формуле левых прямоугольников.

2. В ячейку D6 ввести текст y1,…,yn.

3. Ввести в ячейку D8 формулу =КОРЕНЬ(B8^4-B8^3+8), скопировать эту формулу методом протягивания в диапазон ячеек D9:D17

4. Ввести в ячейку D18 формулу =СУММ(D7:D17).

5. Ввести в ячейку D19 формулу =B4*D18.

6. Ввести в ячейку D20 текст правых.

В итоге получаем следующее:

Ответ: значение заданного интеграла равно 14,45905.

Mathcad

 

Для того, чтобы вычислить интеграл по формуле правых прямоугольников в Mathcad, необходимо выполнить следующие действия:

1. Ввести в поле ввода в одной строчке через какое-либо расстояние следующие выражения: a:=0, b:=3.2, n:=10.

2. В следующей строчке ввести формулу с клавиатуры h:=(b-a)/n (обратить внимание на то, что в поле ввода данное выражение сразу преобразуется к стандартному виду).

3. Рядом вывести значение данного выражения, для этого набрать с клавиатуры: h=.

4. Ниже ввести формулу для вычисления подинтегральной функции, для этого с клавиатуры набрать f(x):=, затем открыть панель инструментов "Арифметика", либо воспользовавшись значком , либо следующим способом:

После этого, на панели инструментов "Арифметика" выбрать "Квадратный корень": , затем в появившемся темном квадрате ввести выражение с клавиатуры x^4-x^3+8, перемещение курсора осуществляется стрелками на клавиатуре (обратить внимание на то, что в поле ввода данное выражение сразу преобразуется к стандартному виду).

5. Ниже ввести выражение I1:=0.

6. Ниже ввести выражение pr_p(a,b,n,h,I1):=.

7. Затем выбрать панель инструментов "Программирование" (либо: "Вид"-"Панели инструментов"-"Программирование", либо: значок ).

8. На панели инструментов "Программирование" добавить строку программы: , затем поставить курсор в первый темный прямоугольник и на панели инструментов "Программирование" выбрать "for".

9. В полученной строке, после слова for, встать курсором в первый из прямоугольников и набрать i.

10. Затем выбрать панель инструментов "Матрицы" (либо: "Вид"-"Панели инструментов"-"Матрицы", либо: значок ).

11. Поставить курсор в следующий темный прямоугольник и на панели инструментов "Матрицы" нажать: , где набрать в двух появившихся прямоугольниках соответственно: 1 и n.

12. Поставить курсор в нижестоящий темный прямоугольник и дважды добавить строку программы.

13. После этого вернуть курсор в первый из появившихся прямоугольников и набрать x1, затем нажать "Локальное присвоение" на панели "Программирование": и после этого набрать a+h.

14. Поставить курсор в следующий темный прямоугольник, где набрать I1 присвоить (кнопка "Локальное присвоение") I1+f(x1).

15. Поставить курсор в следующий темный прямоугольник, где набрать a присвоить (кнопка "Локальное присвоение") x1.

16. В следующем темном прямоугольнике добавить строку программы, где в первом из полученных прямоугольников набрать I1 присвоить (кнопка "Локальное присвоение") I1*h (обратить внимание, что знак умножения в поле ввода автоматически превращается в стандартный).

17. В последнем темном прямоугольнике набрать I1.

18. Ниже ввести pr_p(a,b,n,h,I1) и нажать знак =.

19. Для того, чтобы отформатировать ответ, нужно дважды щелкнуть по полученному числу и указать число десятичный мест - 5.

В итоге получаем:

Ответ: значение заданного интеграла равно 14,45905.

Вывод

Метод прямоугольников безусловно очень удобен при вычислении определенного интеграла. Работа была очень увлекательна и познавательна.

 

Использованная литература

http://www.cleverstudents.ru/method_of_rectangles.html

(методы вычисления интегралов)

http://algmet.narod.ru/theory_a4m/integr_prav/index.htm

(суть метода)

http://ru.wikipedia.org/wiki/%CC%E5%F2%EE%E4_%EF%F0%FF%EC%EE%F3%E3%EE%EB%FC%ED%E8%EA%EE%E2

(википедия)

Содержание

1) введение и теория

2) Суть метода и решение примеров

3) Паскаль

4) Блок-схема

5) Excel

6) MathCad

7) Вывод