Проверка гипотезы о распределении с помощью критерия согласия Пирсона

Курсовая работа по теме

«Статистические методы обработки

Экспериментальных данных»

Выполнил: студент Горелов В.С.

группа ДТпп-2-1

 

Проверил: Климова М.А.

 

 

Вариант № 4

 

 

Москва - 2012

Построение интервальное и точечное статистические распределения результатов наблюдений. Построение полигона и гистограммы относительных частот

 

I - порядковый номер;

- интервал разбиения;

- середина интервала ;

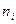- частота;

- относительная частота ( -объем выборки);

-плотность относительной частоты (h - шаг разбиения, т.е. длина интервала );

i
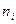
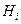
	0;2			0,186666	0,093333
	2;4			0,173333	0,086666
	4;6			0,153333	0,076666
	6;8			0,146666	0,073333
	8;10			0,1	0,05
	10;12			0,073333	0,036666
	12;14			0,053333	0,026666
	14;16			0,04	0,02
	16;18			0,033333	0,016666
	18;20			0,026666	0,013333
	20;22			0,013333	0,006666

 

n= 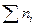- объем выборки;

 

n = =150 ;

 

=0,999996;

 

h = 2.

 

 

 

Гистограмма относительных частот

 

Нахождение точечных оценок математического ожидания и дисперсии

 

 

(выборочная средняя);

 

 

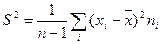(исправленная выборочная дисперсия).

 

 

i
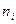
				958,23
				385,385
				78,7175
				0,495
				69,3375
				189,4475
				302,58
				398,535
				515,1125
				590,49
				400,445

 

 

n = =150;

 

å =1028

 

å =3888,775

 

 

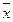=1028/150=6,85

 

 

s² =3888,775/149=26,0991

 

 

Выдвижение гипотезы о распределении случайной величины

 

а) Нормальное (или гауссовское) распределение с параметрами «а» и « 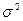», где

 

 

б) Показательное (или экспоненциальное) распределение с параметрами и , где ,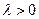

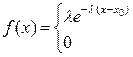
при

при

 

 

в) Равномерное распределение на отрезке [А; В], где

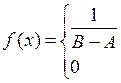
при

 

при x<A и x>B

 

 

Сравнение построенной гистограммы и графиков плотностей основных распределений приводит к заключению о том, что изучаемая случайная величина имеет показательное распределение.

 

Построение графика теоретической плотности распределения

 

Чтобы выписать плотность теоретического (предполагаемого) распределения, нужно определить значения параметров λ и х₀ и подставить их в соответствующую формулу. Все параметры тесно связаны с числовыми характеристиками случайной величины, т.е.

MX = 1/λ+х₀

DX =1/λ²

Поскольку значения математического ожидания и дисперсии неизвестны, то их заменяют соответствующими точечными оценками, т.е. используют (уже упомянутые ранее) приближенные равенства MX » 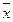, DX » s² , что позволяет найти значения параметров распределения.

 

По исходным данным была выдвинута гипотеза о показательном распределении изучаемой случайной величины. Найдем параметры этого распределения:

 

 

Следовательно, плотность предполагаемого распределения задается формулой

Теперь необходимо вычислить значения теоретической плотности f (x) при (то есть значение в “параметре сдвига”) и при х=х_i где х_i ˃х₀ (то есть значения в серединах интервалов, больших х₀). Для этого воспользуемся следующей схемой (ниже x_j=x₀ или х_j=x_i , где х_i˃x₀):

значения функции e^-u_j

 

		e-uj
1.742			0,19
	-0,049	1,0498	0,1994
	0,239	0,7886	0,1498
	0,619	0,5407	0,1027
	0,999	0,3707	0,0704
	1,379	0,2541	0,0482
	1,759	0,1742	0,0331
	2,139	0,1194	0,0227
	2,519	0,0819	0,0155
	2,899	0,0561	0,0106
	3,279	0,0385	0,0073
	3,659	0,0264	0,0050

Далее, на одном чертеже строим гистограмму и график теоретической плотности распределения: гистограмма была построена ранее, а для получения графика плотности наносим точки с координатами (xi; f(x )) и соединяем их плавной кривой.

 

 

 

Проверка гипотезы о распределении с помощью критерия согласия Пирсона.

Ранее была выдвинута гипотеза о законе распределения рассматриваемой случайной величины. Сопоставление статистического распределения (гистограмма) и предполагаемого теоретического (графика плотности) показывает наличие некоторых расхождений между ними. Поэтому возникает естественный вопрос: чем объясняются эти несовпадения? Ответить на него можно двояко:

1) Указанные расхождения несущественны и вызваны ограниченным количеством наблюдений и случайными факторами – случайностью результата единичного наблюдения, способа группировки данных и т.п. В этом случае выдвинутая гипотеза о распределении считается правдоподобной и принимается как не противоречащая опытным данным.

 

2) Указанные расхождения являются существенными (неслучайными) и связаны с тем, что действительное распределение случайной величины отличается от предполагаемого. В этом случае выдвинутая гипотеза о распределении отвергается как плохо согласующаяся данными наблюдений.

 

Для выбора первого или второго варианта ответа и служат так называемые критерии согласия. Словари толкуют слово критерий (от греч. kriterion – средство для суждения) как признак, на основании которого производится оценка, определение и классификация чего-либо.

Существуют различные критерии согласия: К. Пирсона, А.Н. Колмогорова, Н.В. Смирнова, В.И. Романовского и другие. Мы рассмотрим лишь один из них – критерий Пирсона, называемый также критерием c² («хи - квадрат»).

Критерий Пирсона выгодно отличается от остальных, во – первых, применимостью к любым (дискретным, непрерывным) распределениям и, во – вторых, простотой вычислительного алгоритма.

Правило проверки статистических гипотез с помощью критерия Пирсона будет объяснено на примерах.