Вычисление теоретических частот

Критерий Пирсона основан на сравнении эмпирических (опытных) частот с теоретическими. Эмпирические частоты n_I определяются по фактическим результатам наблюдений. Теоретические частоты, обозначаемые далее , находятся с помощью равенства

= n × p_i ,

где n – количество испытаний, а p_i º R (z_{i –1} < x < z_i) - теоретическая вероятность попадания значений случайной величины в i-й промежуток (1 £ i £ 1).Теоретические вероятности вычисляются в условиях выдвинутой гипотезы о законе распределения изучаемой случайной величины.

В данном варианте принята гипотеза о показательном распределении случайной величины. В этом случае теоретическая вероятность p_i при любом i вычисляется по одной из следующих трех формул (в зависимости от взаимного расположения i-ого промежутка и числа х₀ ):

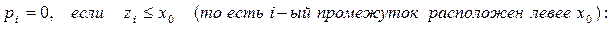
z_i-1 z_i x₀

z_i-1 x₀ z_i

x₀ z_i-1 z_i

Процедура отыскания теоретических вероятностей и частот показана в расчетной таблице:

n = 150;

i	Концы промежутков			e-ui-1	e-ui	Pi= e-ui-1- e-ui	=npi
zi -1	zi
	- ¥	+	0,49 0,43 0,81 1,18 1,56 1,94 2,32 2,71 3,09	0,49 0,43 0,81 1,18 1,56 1,94 2,32 2,71 3,09 +∞	1,0000 0,9524 0,6530 0,4477 0,3069 0,2104 0,1442 0,0989 0,0678 0,0465	0,9524 0,6530 0,4477 0,3069 0,2104 0,1442 0,0989 0,0678 0,0465 0,0000	0,0476 0,2994 0,2053 0,1408 0,0965 0,0662 0,0453 0,0311 0,0213 0,0465	7,14 44,91 30,795 21,12 14,475 9,93 6,795 4,665 3,195 6,975

å: 1 150

5.3 Статистика c² и вычисление ее значения по опытным данным.

Для того чтобы принять или отвергнуть гипотезу о законе распределения изучаемой случайной величины, в каждом из критериев согласия рассматривается некоторая (специальным образом подбираемая) величина, характеризующая степень расхождения теоретического (предполагаемого) и статистического распределения.

В критерии Пирсона в качестве такой меры расхождения используется величина

,

называемая статистикой «хи - квадрат» или статистикой Пирсона (вообще, статистикой называют любую функцию от результатов наблюдений). Ясно, что всегда c² ³0, причем c² = 0, тогда и только тогда, когда при каждом i , т.е. когда все соответствующие эмпирические и теоретические частоты совпадают. Во всех остальных случаях c² ¹ 0; при этом значение c² тем больше, чем больше различаются эмпирические и теоретические частоты.

Прежде чем рассказать о применении статистики c² к проверке гипотезы о закон е распределения , вычислим ее значение для данного варианта; это значение, найденное по данным наблюдений и в рамках выдвинутой гипотезы, будем обозначать через c²_набл..

i	ni
		7,14   44,91   30,795   21,12   14,475   9,93   6,795   4,665   3,195   6,975	60,94392 7,962327 1,973113 0,036667 0,019041 0,115297 0,21369 0,382042 1,019726

: 150 150 72,802

c²_набл. =72,802

5.4. Распределение статистики c².

Случайная величина имеет c² – распределение с r степенями свободы (r = 1; 2; 3; …), если ее плотность имеет вид

где c_r – которая положительная постоянная ( c_r определяется из равенства ). Для дальнейшего изложения важно лишь отметить, что, во – первых, распределение определяется одним параметром – числом r степеней свободы и, во – вторых, существуют таблицы, позволяющие произвольно найти вероятность попадания значений случайной величины в любой промежуток.

Вернемся теперь к статистике . Отметим, что она является случайной величиной, поскольку зависит от результатов наблюдений и, следовательно, в различных сериях опытов принимает различные, заранее не известные значения. Понятно, кроме того, закон распределения статистики зависит: 1) от действительного (но неизвестного нам) закона распределения случайной величины, измерения которой осуществляются (им определяются эмпирические частоты ) ; 2) от количества произведенных наблюдений (от числа n) и от способа разбиения числовой оси на промежутки (в частности, от числа i ); 3) от теоретического (выдвинутого в качестве гипотезы) закона распределения изучаемой случайной величины (им определяются теоретические вероятности p_i и теоретические частоты = n × p_i )

Если выдвинутая гипотеза верна, то очевидно, закон распределения статистики зависит только от закона распределения изучаемой случайной величины, от числа n и от выбора промежутков разбиения. Но на самом же деле, в этом случае (благодаря мастерски подобранному Пирсоном выражению для ) справедливо куда более серьезное утверждение. А именно, при достаточно больших n закон распределения статистики практически не зависит от закона распределения изучаемой случайной величины и ни от количества n произведенных опытов: при распределение статистики стремится к - распределению с r степенями свободы. Эта теорема объясняет, почему статистика Пирсона обозначается через .

Если в качестве предполагаемого выбрано одно их трех основных непрерывных распределений (нормальное, показательное или равномерное), то r = i – 3, где i – количество промежутков, на которые разбита числовая ось (количество групп опытных данных). В общем случае

где 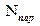- количество параметров предполагаемого (теоретического) распределения, которые заменены вычисленными по опытным данным оценками.

Т.е. в данном варианте после группировки исходных данных получаем количество промежутков разбиения i = 10, 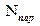= 2, т.к. количество параметров предполагаемого (теоретического) распределения, которые заменены вычисленными по опытным данным оценками, = 2 – это λ и х₀ для показательного распределения.

Следовательно

r = i- 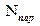-1=10-2-1=7