Методика решения нормальных уравнений

ПРОГРАММИРОВАНИЕ

НА ЯЗЫКЕ ВЫСОКОГО УРОВНЯ

 

 

Методические указания к выполнению курсовой работы

 

 

Санкт-Петербург

 

 

Составитель: Л.А. Прокушев

 

Рецензент: канд. техн. наук доцент В.П. Попов

 

 

Разработка содержит методические указания к выполнению курсовой работы, которые предназначены для закрепления практических навыков
алгоритмизации и программирования на языке высокого уровня с использованием типовых вычислительных методов прикладной математики, модульного принципа программирования и библиотеки стандартных подпрограмм.

Методические указания предназначены для студентов, изучающих дисциплины «Программирование на языке высокого уровня», «Информатика».

Подготовлены к публикации кафедрой компьютерных систем автоматизации. Рекомендованы к изданию редакционно-издательским советом Санкт-Петербургского государственного университета аэрокосмического приборостроения.

 

ã Санкт-Петербургский

государственный университет

аэрокосмического приборостроения, 2002

 

 

Лицензия ЛР № 020341 от 07.05.97 г.

Подписано к печати Формат 60х84 1/16. Бумага тип. №3

Печать офсетная. Усл. печ. л. Уч.-изд. л.

Тираж экз. Заказ №

Редакционно-издательский отдел

Отдел оперативной полиграфии СПбГУАП

190000, Санкт-Петербург, ул. Б. Морская, 67

- 1 -

Цель работы

 

Настоящая курсовая работа является завершающим этапом дисциплины “Программирование на языке высокого уровня” и требует от студента в процессе ее выполнения:

а) практического освоения типовых вычислительных методов прикладной математики;

б) совершенствования навыков разработки алгоритмов и построения программ на языке высокого уровня;

в) освоения принципов модульного программирования и техники использования подпрограмм;

г) исследования нескольких вариантов решения предложенного задания и выбора лучшего варианта по заданному критерию.

Практическое выполнение курсовой работы предполагает решение типовых инженерных задач обработки данных с использованием методов матричной алгебры, решение систем линейных алгебраических уравнений. Навыки, приобретаемые в процессе выполнения курсовой работы, являются основой для использования вычислительных методов прикладной математики и техники программирования в процессе изучения всех последующих дисциплин, а также при выполнении курсовых и дипломных проектов.

 

Выбор математического метода решения задачи

Рекомендации по аппроксимации методом наименьших квадратов

Постановка задачи

 

При изучении зависимостей между величинами важной задачей является приближенное представление (аппроксимация) этих зависимостей с помощью известных функций или их комбинаций, подобранных надлежащим образом. Подход к такой задаче и конкретный метод ее решения определяются выбором используемого критерия качества приближения и формой представления исходных данных.

Пусть изучается связь между величинами C и U, из которых первая рассматривается в качестве независимой переменной, а вторая - ее функции. Исходные данные представлены значениями U, заданными на некотором множестве M значений X. Тогда ошибка приближения этой зависимости некоторой аппроксимирующей функции y = j (x) для каждого из значений X может быть оценена разностью

 

- 2 -

 

d = y - j (x) , x Î M .

 

Возможны случаи дискретного и непрерывного представления М.

1. Значения y = y_i заданы для конечного множества (n) значений x_i , (i=1, 2,…, n) . Тогда для каждого из этих значений определена и ошибка (рис. 1)

d_i = d (x_i ) = y_i – j (x_i) , ( i =1, 2, …, n) . (2.1)

 

y

y = j (x)

y_n

(x_i ,y_i)

_{_}y_i

d_i

y₂

 

y_{1 ­}

x ₁ x ₂ x _i x _n x

Рис. 1. Задание y на дискретном множестве значений x

 

2. Задана функция y=f(x), определяющая значения y для всех точек некоторого интервала [a, b]. Для тех же значений определена и ошибка (рис. 2)

 

d = d (x) = f(x) - j (x) , xÎ [a, b] , (2.2)

 

являющаяся непрерывной функцией x.

y

y = j (x)

y = f (x)

a x b x

Рис. 2. Задание y как непрерывной функции x

- 3 –

 

На основе изучения ошибок d формируются различные критерии качества аппроксимации, служащие для определения наилучшей аппроксимирующей функции j (x). Один из распространенных подходов опирается на использование метода наименьших квадратов (МНК), в соответствии с которым наилучшей считается такая аппроксимирующая функция j (x), для которой достигается наименьшее значение суммы квадратов ошибок d во всех точках x, принимаемых во внимание.

Применительно к случаю 1 это требование принимает вид

. (2.3)

 

В случае 2 операция суммирования в конечном множестве точек должна быть заменена операцией интегрирования квадрата ошибки (2.2) по всему интервалу [a, b] и условие МНК записывается следующим образом:

. (2.4)

 

В настоящей курсовой работе исходные данные заданы в виде табличной зависимости y_i (x_i), то есть рассматривается решение задачи для случая 1. Уточним условия МНК для этой задачи.

 

Задача. Зависимость между переменными x и y задана их значениями в отдельных точках 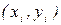, . Требуется найти функцию 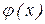, наилучшим образом (в смысле МНК) аппроксимирующую указанную зависимость (см. рис. 1).

 

В соответствии с требованием (2.3) наилучшая аппроксимирующая функция должна быть определена из условия

. (2.5)

 

Подобное задание исходных данных встречается в задачах технических измерений и их статистической обработки, когда для каждого из задаваемых значений осуществляется измерение величины (сопровождающееся возможными ошибками). Аппроксимация позволяет представить изучаемую связь между x и y с помощью известных функций, что облегчает последующее использование данных, кроме того позволяет «сгладить» возможные ошибки измерений, а также дает возможность оценивать значения переменной в точках x интервала , не совпадающих с заданными (т.е. решать задачу интерполяции).

- 4 -

 

Методика выбора аппроксимирующей функции

 

Аппроксимирующую функцию φ(x) выбирают из некоторого семейства функций, для которого задан вид функции, но остаются неопределенными (и подлежат определению) ее параметры С₁, С₂, …, С_m , т.е.

 

j (x) = j (x, С₁, С₂,…, С_m) . (2.6)

 

Определение аппроксимирующей функции φ разделяется на два основных этапа:

· подбор подходящего вида функции φ(х) ;

· нахождение ее параметров в соответствии с критерием МНК.

Подбор вида функции φ(х) представляет собой сложную задачу, решаемую методом проб и последовательных приближений. Исходные данные, представленные в графической форме (семейства точек или кривые), сопоставляются c семействами графиков ряда типовых функций, используемых обычно для целей аппроксимации. Некоторые типы функций φ(х), которые можно использовать в курсовой работе, приведены в табл. 1.

 

Таблица 1

Вид функции Название функции

 

 

Более подробные сведения о поведении функций, которые могут быть использованы в задачах аппроксимации, можно найти в справочной литературе [1, c. 126 – 137]. В настоящей курсовой работе вид аппроксимирующей функции φ(х) задан.

- 5 -

 

Общая методика решения

 

После того как выбран вид аппроксимирующей функции φ(х) (или эта функция задана) и, следовательно, определена функциональная зависимость (2.6), необходимо найти в соответствии с требованиями МНК значения параметров С₁, С₂, …, С_m .

Как уже указывалось, параметры должны быть определены таким образом, чтобы значение критерия в рассматриваемой задаче (2.5) было наименьшим по сравнению с его значениями при других возможных значениях параметров.

Для решения задачи подставим выражение (2.6) в выражение (2.5) и проведем необходимые операции суммирования. В результате величина J , именуемая в дальнейшем критерием аппроксимации, представится функцией искомых параметров

J = J(С₁, С₂, …, С_m) . (2.7)

Последующие действия сводятся к отысканию минимума этой функции J переменных С_k . Определение значений С_k = С_k^* , k = 1, 2, …, m , соответствующих этому минимуму J,и является целью решаемой задачи.

Возможны следующие два подхода к решению этой задачи: использование известных условий минимума функции нескольких переменных или непосредственное отыскание точки минимума функции каким-либо из численных методов.

Для реализации первого из указанных подходов воспользуемся необходимыми условиями минимума функции (2.7) нескольких переменных [4, c. 21 – 26], в соответствии с которыми в точке минимума должны быть равны нулю частные производные этой функции по всем ее аргументам

 

∂J / ∂C_k = 0 , (k = 1, 2, …, m) . (2.8)

 

Полученные m равенств следует рассматривать как систему уравнений относительно искомых значений С₁, С₂ ,…, С_m. При произвольном виде функциональной зависимости (2.6) уравнения (2.8) оказываются нелинейными относительно величин С_k , и их решение требует применения приближенных численных методов.

Используемые равенства (2.8) дают лишь необходимые, но не достаточные условия минимума функции (2.7). Поэтому требуется уточнить, обеспечивают ли найденные значения С_k^* именно минимум функции J(С₁, С₂, …, С_m). В общем случае такое уточнение выходит за рамки данной курсовой работы, и предлагаемые для курсовой работы задания подобраны так, что найденное решение системы (2.8) отвечает именно минимуму J. Однако, поскольку величина J неотрицательна (как сумма квадратов) и нижняя ее гра-

- 6 -

 

ница есть 0 (J=0), то, если существующее решение системы (2.8) единственно, оно отвечает именно минимуму J.

Уравнения (2.8), встречающиеся в МНК, называются нормальными, поэтому описываемый способ решения задачи условимся называть методом нормальных уравнений.

Структура этих уравнений получается более простой в том важном частном случае, когда аппроксимирующая функция j(x) выбирается линейной функцией искомых параметров С_k и выражение (2.6) имеет вид

 

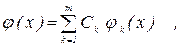(2.9)

где С_k – определяемые параметры; j₁(x), j₂(x),…, j_m(x) – система некоторых линейно-независимых функций, называемых в курсовой работе базисными функциями.

Замечание. Функции j₁(x), j₂(x),…, j_m(x) называются линейно-независимыми, если при любых x равенство

справедливо только тогда, когда все С_k =0.

 

В этом случае, подставляя (2.9) в выражение (2.5) и выполняя дифференцирование в соответствии с (2.8), получим систему уравнений относительно искомых С_k .

Покажем получение системы нормальных уравнений в общем случае для m базисных функций. Раскроем выражение аппроксимирующей функции

j(x) = С₁ j₁(x) + С₂ j₂(x) +…+ С_m j_m(x)

и подставим его в формулу критерия аппроксимации (2.5)

. (2.10)

Применим операцию дифференцирования (2.8) к параметру С₁ :

и, выполняя необходимые алгебраические преобразования, получим уравнение

 

Аналогичные уравнения можно получить, применяя описанные выше операции по отношению к переменным С₂ ,…,С_m . Эти уравнения образуют систему нормальных уравнений:

 

- 7 -

 

a₁₁ С₁ + a₁₂ С₂ +…+ a_1m С_m = b­₁

a₂₁ С₁ + a₂₂ С₂ +…+ a_2m С_m = b­₂ (2.11)

_{……………………………………………………………..}

a_m1 С₁ + a_m2 С₂ +…+ a_{m m} С_m = b­_m ,

 

где коэффициенты a_{k l} и величины b_k (k, l = 1, 2,…, m) определяются выражениями

(2.12)

Уравнения (2.11) представляют собой систему линейных алгебраических уравнений, основные методы решения которых описываются в разд. 2.2.

Преимущество использования линейного представления (2.9) аппроксимирующей функции j (x) состоит в том, что в этом случае однозначно решается вопрос о минимуме величины J. Действительно, если решение системы линейных уравнений (2.11) существует, то оно единственно [3, с.227], поэтому необходимые условия (2.8) являются в данном случае и достаточными условиями минимума функции J(С₁, С₂ ,…, С_m).

 

 

Методика решения нормальных уравнений

 

Один из возможных способов минимизации критерия аппроксимации (2.7) предполагает решение системы нормальных уравнений (2.11). При выборе в качестве аппроксимирующей функции линейной функции искомых параметров (2.9) нормальные уравнения представляют собой систему линейных алгебраических уравнений (2.11).

 

Формы записи системы линейных алгебраических уравнений

 

Систему n линейных уравнений общего вида (где через x_k обозначены искомые параметры С_k аппроксимирующей функции)

 

a₁₁ x₁ + a₁₂ x₂ +…+ a_1n x_n = b­₁

a₂₁ x₁ + a₂₂ x₂ +…+ a_2n x_n = b­₂ (2.13)

_{…………………………………………..}

a_n1 x₁ + a_n2 x₂ +…+ a_{n n} x_n = b­_n

 

можно записать посредством матричных обозначений в следующем виде:

 

A X = B, где

- 8 -

 

(2.14)

 

Квадратная матрица A называется матрицей системы, вектор X – вектором-столбцом неизвестных системы, а вектор B – вектором-столбцом свободных членов.

В матричном представлении исходная система линейных уравнений примет вид

(2.15)

 

Решение системы линейных уравнений сводится к отысканию значений элементов вектора-столбца (x_i), называемых корнями системы. Для получения единственного решения системы входящие в нее n уравнений должны быть линейно независимыми. Необходимым и достаточным условием этого является неравенство нулю определителя данной системы, т.е.
det A ¹ 0.

Алгоритмы решения систем линейных уравнений подразделяются на прямые (конечные) и итерационные (бесконечные). На практике ника­кой метод не может быть бесконечным. Для получения точного решения итерационные методы требуют бесконечного числа арифметических опе­раций. Практически это число приходится брать конечным, и поэтому решение в принципе имеет некоторую ошибку (конечную точность), даже если пренебречь ошибками округлений, сопровождающими большин­ство вычислений. Что же касается прямых методов, то они даже при конечном числе операций могут в принципе (с точностью до ошибок округления) дать точное решение, если оно существует.

 

Решение системы уравнений прямыми методами

 

Прямые, или конечные, методы позволяют найти решение системы уравнений за конечное число шагов. Это решение будет точным, если все промежуточные вычисления выполняются без округления (точно), и приближенным, если вычисления проводятся с ограниченной точ­ностью (как на современных ЭВМ).

- 9 -

 

Одним из наиболее широко используемых прямых методов является метод последовательного исключения неизвестных, или метод Гаусса. Согласно этому методу, исходная система линейных уравнений (2.13) преобразуется путем последовательного исключения неизвестных в эквивалентную систему уравнений, имеющую так называемый «треугольный» вид. Последнее уравнение «тре­угольной» системы содержит лишь одно неизвестное (x_n), предпоследнее – два (x_n, x_n-1) и т.д. Решение полученной системы уравне­ний осуществляется последовательным («снизу вверх») определением x_n из последнего уравнения «треугольной» системы, x_n-1изпредпоследнего и т.д. Применительно к системе уравнений (2.13) преобразование к «треугольному» виду осуществляется за (n – 1) шагов.

На первом шаге выделяется первое уравнение системы (2.13). Это уравнение не преобразуется, и оно объявляется ведущим уравнением. Затем исключается неизвестное x₁ из всех уравнений, кроме веду­щего. Для этого последовательно из каждого уравнения вычитается ведущее уравнение, умноженное на некоторый специально подобранный множитель, позволяющий сделать результирующий коэффициент при x₁ равным нулю. Так, например, для исключения x₁ из второго уравнения

 

a₂₁ x₁ + a₂₂ x₂ + …+ a_{2 n} x_n = b₂

 

необходимо из него вычесть ведущее уравнение, умноженное на коэффициент q₂₁ = a₂₁ / a₁₁. Действительно, результат вычитания имеет вид

 

(a₂₁ – q₂₁ a­₁₁) x₁ + (a₂₂ – q₂₁ a­₁₂) x₂ + …+ (a_2n – q₂₁ a­_1n) x_n =
= b₂ – q₂₁ b₁ . (2.16)

 

Очевидно, что коэффициент (a₂₁ – q₂₁ a₁₁ ) при x₁ равен ну­лю. Вводя новые обозначения для коэффициентов

k=(2, …, n) ,

и свободного члена

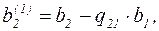
можно переписать уравнение (2.16) в виде

 

 

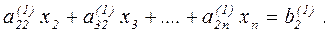
Аналогичную процедуру можно проделать с третьим уравнением системы (2.13). Умножая ведущее уравнение на q₃₁=a₃₁ /a₁₁ и вы­читая результат умножения из третьего уравнения, получим эквива­лентное уравнение

- 10 -

 

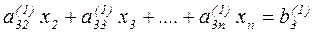и т.д.

В результате рассмотренного первого шага исходная система уравнений (2.13) превратится в эквивалентную систему уравнений, причем неизвестное x₁ входит только в первое уравнение:

 

(2.17)

 

На втором шаге ведущим объявляется второе уравнение системы (2.17) и исключается неизвестное x₂ из уравнений с номерами от третьего до последнего. Исключение неизвестного проводится по схеме, описанной в первом шаге. Для исключения x₂ из третьего уравнения системы (2.17) ведущее уравнение умножается на

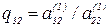
и результат умножения вычитается из третьего уравнения, результирующий коэффициент при x₂ будет равен нулю. Для исключения x₂ из четвертого уравнения ведущее уравнение умножается на

и т.д. В результате второго шага (исключения неизвестного x₂) будет получена система урав­нений, также эквивалентная исходной системе (2.13):

 

(2.18)

 

где введены новые обозначения для коэффициен­тов преобразуемых уравнений. Отметим, что неизвестное x₁ вхо­дит только в первое уравнение, а неизвестное x₂ - в первое и второе уравнения.

 

- 11 -

 

На (n-1) шаге исключается неизвестное x_n-1 из последнего n-го уравнения, и в результате система уравнений принимает окончательный «треугольный» вид

(2.19)

 

Полученная система уравнений эквивалентна исходной системе уравнений (2.13). Описанный процесс последовательного исключения неизвестных носит название прямого хода метода Гаусса.

Определим обобщенные формулы для расчета коэффициентов системы в процессе прямого хода метода Гаусса. На i-м шаге неизвестное x_i исключается из всех уравнений с номерами k, где i+1 £ k £ n, при этом ведущее уравнение (с номером i) умножается на

,

 

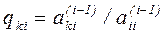и результат умножения вычитается из k-го уравнения. Новые значения коэффициентов (в уравнении с номером k) при неизвестных x_j, (i+1 £ j £ n) равны

 

(2.20)

новое значение свободного члена

. (2.21)

Решение треугольной системы уравнений (2.19) носит название обратного хода метода Гаусса и заключается в последовательном определении всех неизвестных, начиная с последнего x_n. Действительно, из последнего уравнения системы (2.19) вытекает, что

Значение x_n-1 получается при решении предпоследнего уравнения

 

.

 

Так как x_n уже определено, то

- 12 -

 

Эта процедура применяется последовательно ко всем уравнениям, включая и первое, из которого определяется

Обобщенная формула вычисления x_i имеет вид

 

(2.22)

 

В процессе прямого хода метода Гаусса может оказаться, что коэффициент a_ij^(i-1) ведущего уравнения равен нулю. Тогда исключить x_iиз остальных уравнений описанным методом нельзя. Однако уравнения системы можно поменять местами и объявить ведущим то уравнение, у которого коэффициент при неизвестном x_i отличен от нуля. Отметим, что системы, отличающиеся лишь взаимным расположением образующихих уравнений, являются эквивалентными. Перестановка уравнений не только допустима, но часто и полезна для уменьшения погрешности арифметических вычислений. (Напомним, что точность проведения арифметических вычислений на современных ЭВМ всегда ограничена. Это приводит к тому, что при большом числе арифметических операций погрешность ре­зультата может быть весьма значительна.) Для уменьшения погрешности вычислений в качестве ведущего обычно выбирается уравнение с максимальным по модулю коэффициентом при x_i. Это уравнение и уравнение с номером i меняют местами, и процесс исключения продолжается обычным образом. Поиск максимального по модулю коэффициента приx_i носит название определение ведущего элемента.

 

Описание алгоритма решения системы линейных уравнений
методом Гаусса

 

Обобщенная схема алгоритма решения системы уравнений методом последовательного исключения неизвестных представлена на рис. 3.

 

 

Рис. 3. Обобщенная схема алгоритма (метод Гаусса)

- 13 -

 

В результате прямого хода система уравнений (2.13) преобразуется в треугольную систему уравнений (2.19). В процессе обратного хода последовательно определяются все неизвестные, начиная с x­_n .

Для описания алгоритма введем следующие обозначения:

n – порядок системы уравнений;

A – квадратная матрица размера n ´ n , элементы которой первоначально равны коэффициентам системы уравнений (2.13), а далее, в процессе прямого хода – коэффициентам преобразованных систем (2.17) – (2.19);

X – вектор размера n, являющийся решением системы уравнений (2.13).

На рис. 4 представлена схема алгоритма прямого хода метода Гаусса. Переменная i – номер шага исключения, неизвестное X[i] исключается из уравнений с номерами k, принимающими значения от (i+1) до n. Из приведенного выше описания процедуры прямого хода следует, что исключение неизвестного X[i] требует преобразования коэффициентов и свободных членов системы уравнений, то есть матрицы A и вектора B. Каждый шаг исключения состоит из определения ведущего элемента, перестановки уравнений местами и преобразования коэффициентов системы. На
рис. 4 k обозначает номер преобразуемого уравнения системы, i+1 £ k £ n.

Под ведущим элементом на i-м шаге исключения принимается максимальный по модулю коэффициент при неизвестном X[i], то есть максимальный по модулю элемент последовательности А[i, i], A[i+1, i],…, А[n-1, i], A[n, i]. На схеме алгоритма (рис. 5) переменная big – величина этого максимума, а переменная num – его номер, то есть

big = A[num, i] = max | A[l, i] | .

i£ l£ n

Равенство переменной num нулю означает, что для любого l при
i£ l£ n коэффициенты системы A[l, i] = 0, и, следовательно, неизвестное X[i] не входит в оставшиеся уравнения системы. В этом случае определитель матрицы А равен нулю, и, как известно, существование бесконечного числа решений или отсутствие последнего зависит от вида правой части системы (2.13) – вектора В. В обоих случаях процедура прямого хода метода Гаусса прекращается (завершается «аварийно»), и необходимы другие методы исследования и получения решения (если оно вообще существует).

В практически используемых программах вычисления по методу Гаусса обычно задается некоторое малое число eps, и если окажется, что big<eps, то это свидетельствует о практической вырожденности системы уравнений (2.13) и о неприменимости метода Гаусса.

После определения ведущего элемента (см. рис. 5), необходимо поменять местами уравнения с номерами i и num (рис. 6), что фактически означает автоматически перестановку двух строк (с номерами i и num) матрицы А и элементов B[i] и B[num] вектора В. Такая перестановка требует дополнительной переменной (переменная temp на рис. 6) для временного хранения

- 14 -

 

переставляемого значения. Если i=num, то ведущим является само уравнение с номером i , и перестановка не нужна.

Исключение неизвестного X[i] из уравнения с номером k представлено на рис. 7. Напомним, что исключение переменной сводится к определению новых значений элементов k-й строки матрицы А и элемента В[k]. Переменная Q – множитель q_ki, на который умножается ведущее уравнение. Он выбирается не зависящим от индексов k и i, так как необходим только для вычисления коэффициентов k-й строки и хранить постоянно его не нужно. Элемент A[k, i] должен стать равным нулю, поэтому нулевое значение присваивается ему непосредственно, а не в результате вычисления

A[k, i]= A[k, i] – Q× A[i, i],

так как в силу ошибок округления при выполнении арифметических операций может оказаться, что последняя величина отлична от нуля.

Обратный ход метода Гаусса (рис. 8) начинается с определения X[n], а далее последовательно определяются неизвестные X[i], i=n – 1, n – 2, …, 1 по формуле (2.22).