Коэффициент детерминации

После проверки значимости каждого коэффициента регрессии обычно проверяется общее качество уравнения регрессии, которое оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Другими словами, насколько широко рассеяны точки наблюдений относительно линии регрессии. Очевидно, если все точки лежат на построенной прямой, то регрессия Y на X «идеально» объясняет поведение зависимой переменной. В реальной жизни такая ситуация практически не встречается обычно поведение Y лишь частично объясняется влиянием переменной X.

Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В математической статистике дисперсионный анализ рассматривается как самостоятельный метод статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.

Рассмотрим вариацию (разброс) значений y_i вокруг среднего значения . Разобьём эту вариацию на две части: объяснённую регрессионным уравнением и не объяснённую (т.е. связанную с ошибками e_i). Тогда получим

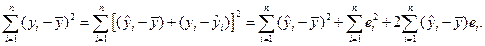(5.45)

Покажем, что третье слагаемое будет равно нулю:

.

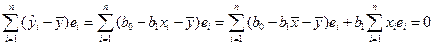Здесь учтено свойства ошибки e_i: 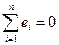и .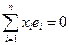

Таким образом, справедливо следующее равенство

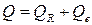, (5.46)

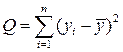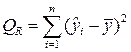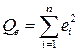где – общая сумма квадратов отклонений зависимой переменной от средней, а и – соответственно, сумма квадратов, обусловленная регрессией, и сумма квадратов, характеризующая влияние неучтенных факторов.

Замечание 1. В англоязычной литературе Q, Q_R, Q_e часто обозначаются соответственно TSS (total sum of squares), RSS (regression sum of squares) и ESS (error sum of squares), хотя эти обозначения не являются общепринятыми.

Замечание 2. Равенство (5.46) верно только в том случае, когда константа b₀ включена в число объясняющих параметров регрессии.

Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле

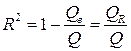. (5.47)

Заметим, что второе равенство в (5.47) верно лишь в том случае, если верно (5.46), т.е. когда константа включена в уравнение регрессии. Только в этом случае имеет смысл рассматривать статистику R².

В силу определения R² принимает значения между 0 и 1, 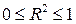. Чем ближе R² к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если R²=1, то эмпирические точки (x_i,y_i) лежат на линии регрессии и между переменными Y и X существует линейная функциональная зависимость. Если R²=0, то вариация зависимой переменной полностью обусловлена воздействием неучтённых в модели переменных, и линии регрессии параллельна оси абсцисс. Величина R² показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.

Не следует однако абсолютизировать высокие значения R², т.к. коэффициент детерминации может быть близким к единице в силу того, что обе исследуемые величины X и Y имеют выраженный временной тренд, не связанный с их причинно-следственной зависимостью. В экономике обычно такой тренд имеют объёмные показатели (ВНП, ВВП, доход, потребление). А темповые и относительные показатели (темпы роста, производительность, ставка процента) не всегда имеют тренд. Поэтому при оценивании регрессий по временным рядам объёмных показателей (например, зависимость потребления от дохода или спроса от цены) величина R² может быть весьма близкой к единице. Но это не обязательно свидетельствует о наличии значимой линейной связи между исследуемыми показателями, а может лишь означать лишь то, что поведение зависимой переменной нельзя описать уравнением .

Если уравнение регрессии строится по перекрестным данным, а не по временным рядам, то коэффициент детерминации R² для него обычно не превышает 0,6-0,7. Аналогичные значения R² обычно получаются и для регрессий по временным рядам, если они не имеют выраженного тренда (темп инфляции от уровня безработицы, темпы прироста выпуска от темпов прироста затрат ресурсов и т.п.).

В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, т.е. R²=r².

% Действительно,

. &

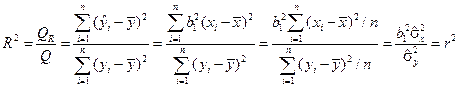Пример 5.5. По данным примеров 5.1-5.4 рассчитать коэффициент детерминации R².

Решение. По формуле (5.71) находим

.

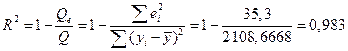Столь высокое значение коэффициента детерминации свидетельствует о высоком общем качестве построенного уравнения регрессии. Отметим, что коэффициент детерминации можно было вычислить и иначе: 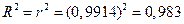. â

5.3.2. Проверка общего качества уравнения регрессии:
F-тест

Любая сумма квадратов отклонений связана с числом степеней свободы (df – degrees of freedom), т.е. с числом независимого варьирования переменной. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых отклонений из n возможных 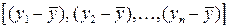требуется для образования данной суммы квадратов. Так, для общей суммы квадратов 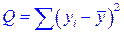требуется (n–1) независимых отклонений, ибо по совокупности из n единиц после расчета среднего значения свободно варьируются лишь (n–1) число отклонений. Это связано с тем, что 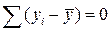, поэтому если известны (n–1) отклонений, то n-ое отклонение может быть уже вычислено.

При расчёте объяснённой или факторной суммы квадратов 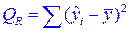используются теоретические (расчётные) значения результативного признака 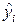, найденные по линии регрессии. В линейной регрессии 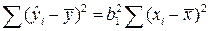, следовательно, при заданном объёме наблюдений по x и y факторная сумма квадратов при линейной регрессии зависит только одной константы коэффициента регрессии b₁, то данная сумма квадратов имеет одну степень свободы. К этому же выводу можно прийти и по другому. Величина 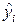определяется по уравнению линейной регрессии: 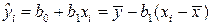. Отсюда видно, что при заданном наборе переменных x и y расчётное значение 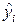является в линейной регрессии функцией только одного параметра – коэффициента регрессии. Соответственно и факторная сумма квадратов отклонений имеет число степеней свободы, равно 1.

Число степеней свободы остаточной суммы квадратов 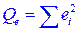для линейной регрессии, как мы видели, равна (n–2). Между числом степеней свободы общей, факторной и остаточной суммами квадратов существует взаимосвязь. Число степеней свободы для общей суммы квадратов равно сумме степеней свободы для факторной и остаточной сумм квадратов: .

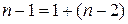Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.

, , .

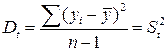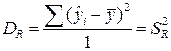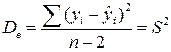Определение дисперсии на одну степень свободы приводит дисперсии к сравниваемому виду.

При отсутствии линейной зависимости между зависимой и объясняющей переменными случайные величины 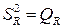и 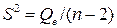имеют c²-распределение соответственно с 1 и n–2 степенями свободы. Сопоставляя факторную и остаточную дисперсии в расчёте на одну степень свободы, получим случайную величину, описывающуюся распределением Фишера с теми же степенями свободы:

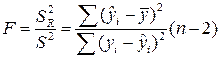. (5.48)

Полученную F-статистику можно использовать для проверки нулевой гипотезы 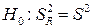. Для линейной регрессии критерий (5.48) можно записать в виде

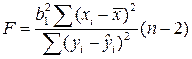, (5.49)

поэтому нулевой гипотезе можно придать вид 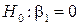. Таким образом, значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с её средней.

Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга, т.е. 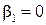. Эмпирическое уравнение регрессии значимо на уровне a, если фактически наблюдаемое значение статистики

,

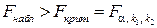где 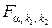– табличное значение F-критерия Фишера, определённое на уровне значимости a при k₁=1 и k₂=n–2 степенях свободы.

Величина F-критерия связана с коэффициентом детерминации R². Факторную сумму квадратов отклонений можно представить как

,

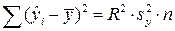а остаточную сумму квадратов – как

.

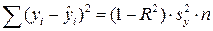Тогда значение F-критерия можно выразить как

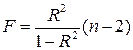. (5.50)

Таким образом, F-критерий является также критерием для проверки значимости коэффициента детерминации R².

5.3.3. Проверка общего качества уравнения регрессии:
t-тест

Следует отметить, что значимость уравнения парной линейной регрессии может быть проведена и другим способом, если оценить значимость коэффициента регрессии b₁, который, как уже отметалось, имеет распределение Стьюдента с n–2 степенями свободы.

Уравнение парной линейной регрессии или коэффициент регрессии b₁ значимы на уровне a (иначе – гипотеза H₀ о равенстве коэффициента b₁нулю, т.е. 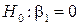, отвергается), если фактически наблюдаемое значение статистики

(5.51)

больше критического (по абсолютной величине), т.е. .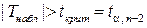

Если сравнить (5.50) и (5.52), то можно заметить, что

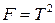. (5.52)

Следовательно, для парной линейной модели оба способа проверки значимости с использованием F- и t-критериев равносильны.

Пример 5.6. По данным примеров 5.1-5.5 проверить значимость построенного уравнения регрессии.

Решение. По формуле (5.50) находим

.

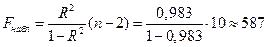На уровне значимости a=0,05 и числе степеней свободы k₁=1 и k₂=10 получим

.

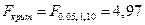Поскольку F_набл>F_крит, то можно сделать вывод о значимости уравнения регрессии на уровне значимости 0,05. Отметим также, что для коэффициента b₁ t-критерий равен

.

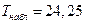Как легко заметить, что для данного случая 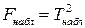. â