 |
Главная |
Следствия из второго замечательного предела
|
из
5.00
|
· 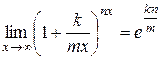 .
.
Действительно, 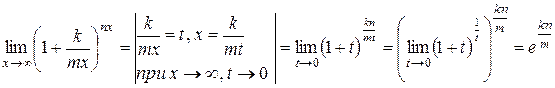 .
.
· 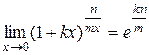 .
.
Действительно, 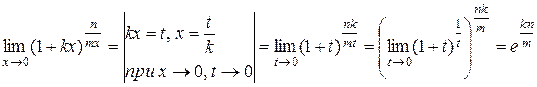 .
.
· 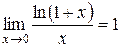 .
.
Данный предел содержит неопределённость вида 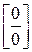 . По свойствам логарифма данный предел можно переписать в виде
. По свойствам логарифма данный предел можно переписать в виде 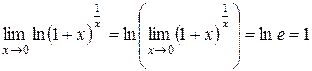
· 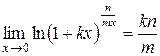 .
.
Действительно, 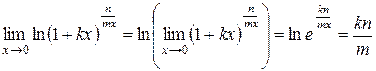 .
.
6.4
Функция 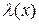 называется бесконечно малой при
называется бесконечно малой при 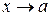 , если
, если 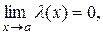 т.е.
т.е. 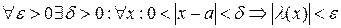
 .
.
Функция 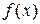 называется ограниченной при
называется ограниченной при 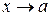 , если существуют такие положительные числа
, если существуют такие положительные числа 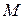 и
и 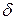 , такие, что при условии
, такие, что при условии 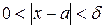 выполняется неравенство
выполняется неравенство 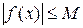 . В противном случае функция называется неограниченной. Любая бесконечно малая функция является ограниченной при
. В противном случае функция называется неограниченной. Любая бесконечно малая функция является ограниченной при 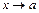 .
.
Функция 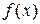 называется бесконечно большой при
называется бесконечно большой при 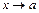 , если для любого числа
, если для любого числа 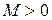 существует такое число
существует такое число 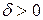 , что
, что 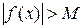 для всех
для всех 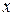 удовлетворяющих неравенству
удовлетворяющих неравенству 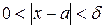 . Обозначают
. Обозначают 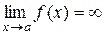 .
.
Если при этом 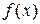 положительна (отрицательна) в
положительна (отрицательна) в 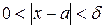 , то пишут
, то пишут 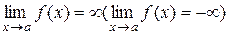 . Бесконечно большая функция
. Бесконечно большая функция 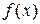 при
при 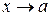 не имеет предела (если записано
не имеет предела (если записано 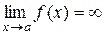 , то здесь
, то здесь 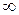 - не число, а обозначение факта, что
- не число, а обозначение факта, что 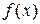 - бесконечно большая функция).
- бесконечно большая функция).
Свойства бесконечно малых и бесконечно больших функций.
1. Если функция 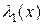 и
и 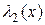 являются бесконечно малыми, то функция
являются бесконечно малыми, то функция 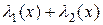 также бесконечно малая.
также бесконечно малая.
2. Произведение ограниченной при 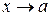 функции на бесконечно малую есть функция бесконечно малая.
функции на бесконечно малую есть функция бесконечно малая.
3. Произведение постоянной на бесконечно малую есть бесконечно малая функция.
4. Произведение двух бесконечно малых функций есть бесконечно малая функция.
5. Если функция 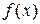 бесконечно большая, то
бесконечно большая, то 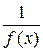 - бесконечно малая.
- бесконечно малая.
6. Если функция 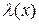 - бесконечно малая и
- бесконечно малая и 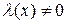 , то
, то 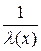 - бесконечно большая.
- бесконечно большая.
7. Для того, чтобы число 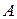 было пределом функции
было пределом функции 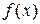 при
при 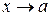 , необходимо и достаточно, чтобы эта функция была представима в виде
, необходимо и достаточно, чтобы эта функция была представима в виде 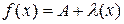 , где
, где 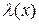 - бесконечно малая.
- бесконечно малая.
Пусть функции 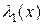 и
и 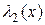 являются бесконечно малыми при
являются бесконечно малыми при 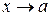 . Рассмотрим
. Рассмотрим 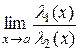 . Если
. Если
· 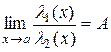 , где
, где 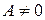 и
и 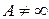 , то говорят, что
, то говорят, что 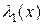 и
и 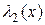 - бесконечно малые одного порядка малости (при
- бесконечно малые одного порядка малости (при 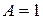
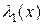 и
и 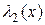 - эквивалентные бесконечно малые);
- эквивалентные бесконечно малые);
· 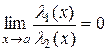 , то говорят, что
, то говорят, что 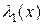 бесконечно малая более высокого порядка малости по сравнению с
бесконечно малая более высокого порядка малости по сравнению с 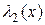 ;
;
· 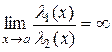 то говорят, что
то говорят, что 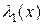 бесконечно малая более низкого порядка малости по сравнению с
бесконечно малая более низкого порядка малости по сравнению с 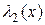 .
.
6.5
К абстракции непрерывности человек пришел, наблюдая окружающие его сплошные среды – твердые (например, металлы), жидкие (например, вода), газообразные (например, воздух). На самом деле, всякая физическая среда состоит из скопления большого числа отделенных друг от друга движущихся частиц. Однако эти частицы и расстояния между ними настолько малы по сравнению с объемами сред, с которыми приходиться иметь дело в макроскопических физических явлениях, что многие такие явления можно достаточно хорошо изучать, если считать приближенно массу изучаемой среды непрерывно распределенной без всяких просветов в занятом ею пространстве. На таком допущении базируются многие физические, химические и естественно научные дисциплины. Математическое понятие непрерывности играет в этих дисциплинах большую роль.
Непрерывная функция математически выражает свойство, с которым часто приходиться встречаться на практике, заключающееся в том, что малому приращению независимой переменной соответствует малое приращение зависимой переменной. Примерами подобных процессов могут служить законы движения тела, выражающие зависимости пути, пройденного телом, от времени. Тот или иной закон движения устанавливает между ними определенную непрерывную связь, характеризующуюся тем, что малому приращению времени соответствует малое приращение пути.
Разрывные функции в математике отражают скачкообразные процессы, встречающиеся в природе. При ударе, например, скорость тела меняется скачкообразно. Многие качественные переходы сопровождаются скачками.
Перейдем к математическому определению вводимых понятий.
Пусть функция 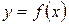 задана в некотором интервале,
задана в некотором интервале, 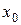 и
и 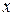 - два значения аргумента из этого интервала. Тогда при переходе от точки
- два значения аргумента из этого интервала. Тогда при переходе от точки 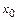 к точке
к точке 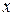 будем говорить, что аргумент получил приращение
будем говорить, что аргумент получил приращение 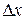 , т.е. величину
, т.е. величину 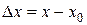 будем называть приращением аргумента. Соответственно разность
будем называть приращением аргумента. Соответственно разность 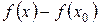 будем называть приращением функции и обозначать
будем называть приращением функции и обозначать 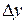 , т.е.
, т.е. 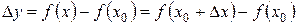 .
.
Функция 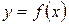 называется непрерывной в точке
называется непрерывной в точке 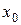 , если она определена в некоторой окрестности точки
, если она определена в некоторой окрестности точки 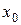 , включая саму эту точку, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке, т.е.
, включая саму эту точку, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке, т.е.
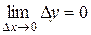 , или
, или 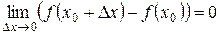 .
.
Отсюда, условие непрерывности можно записать и так:
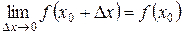 , или
, или 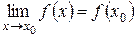 , т.е.
, т.е.
функция 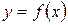 непрерывна в точке
непрерывна в точке 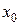 , если предел функции в точке
, если предел функции в точке 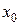 равен значению функции в этой точке.
равен значению функции в этой точке.
Для непрерывности функции 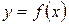 в точке
в точке 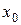 необходимо и достаточно выполнение следующих условий:
необходимо и достаточно выполнение следующих условий:
1) функция должна быть определена в некотором интервале, содержащем точку 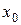 (т.е. в самой точке
(т.е. в самой точке 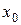 и вблизи этой точки);
и вблизи этой точки);
2) функция должна иметь одинаковые односторонние пределы, т.е. 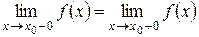 ;
;
3) эти односторонние пределы должны быть равны значению функции в точке 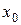 , т.е.
, т.е.
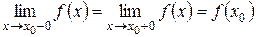 .
.
Функция непрерывная в каждой точке некоторого интервала называется непрерывной на этом интервале. Функция 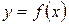 называется непрерывной на отрезке
называется непрерывной на отрезке 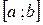 , если она непрерывна в интервале
, если она непрерывна в интервале 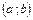 и непрерывна в точке
и непрерывна в точке 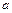 справа и в точке
справа и в точке 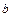 слева.
слева.
Для непрерывных функций в точке справедливы следующие свойства:
· Если функции 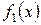 и
и 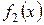 непрерывны в точке
непрерывны в точке 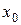 , то непрерывны в этой точке также функции
, то непрерывны в этой точке также функции 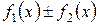 ,
, 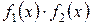 ,
, 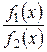 , если
, если 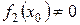 .
.
· Если функция 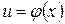 непрерывна в точке
непрерывна в точке 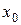 , а функция
, а функция 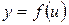 непрерывна в точке
непрерывна в точке 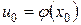 , то сложная функция
, то сложная функция 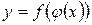 непрерывна в точке
непрерывна в точке 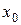 .
.
· Если 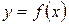 - непрерывная функция, имеющая однозначную обратную функцию, то обратная функция тоже непрерывна.
- непрерывная функция, имеющая однозначную обратную функцию, то обратная функция тоже непрерывна.
· Все элементарные функции непрерывны в каждой точке, где они определены.
Следствие. Всякая элементарная функция непрерывна во всех точках, принадлежащих ее области определения.
· Функция 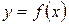 , непрерывная в точке
, непрерывная в точке 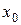 , не равная нулю в этой точке, сохраняет знак
, не равная нулю в этой точке, сохраняет знак 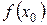 в некоторой точки
в некоторой точки 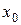 .
.
Рассмотрим некоторые свойства функций, непрерывных на отрезке.
· Если функция 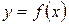 непрерывна на отрезке
непрерывна на отрезке 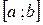 , то на этом отрезке найдутся точки
, то на этом отрезке найдутся точки 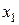 и
и 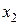 , что значения в этих точках будут соответственно наибольшим и наименьшим на отрезке
, что значения в этих точках будут соответственно наибольшим и наименьшим на отрезке 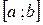 (теорема Вейерштрасса).
(теорема Вейерштрасса).
· Если функция 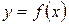 непрерывна на отрезке
непрерывна на отрезке 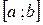 , то она ограничена на нем (следствие теоремы Вейерштрасса).
, то она ограничена на нем (следствие теоремы Вейерштрасса).
· Если функция 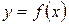 непрерывна на отрезке
непрерывна на отрезке 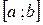 и на концах его принимает значения разных знаков, то между точками
и на концах его принимает значения разных знаков, то между точками 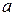 и
и 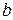 найдется точка
найдется точка 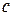 , такая, что
, такая, что 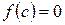 .
.
· Если функция 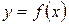 определена и непрерывна на отрезке
определена и непрерывна на отрезке 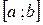 , причем на концах этого отрезка функция принимает неравные значения
, причем на концах этого отрезка функция принимает неравные значения 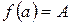 ,
, 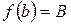 . Тогда для любого числа
. Тогда для любого числа 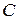 , заключенного между числами
, заключенного между числами 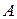 и
и 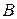 , найдется точка
, найдется точка 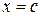 между
между 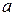 и
и 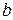 , что
, что 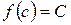 (теорема Коши о промежуточных значениях). Таким образом, непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
(теорема Коши о промежуточных значениях). Таким образом, непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Если функция 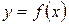 не является непрерывной в точке
не является непрерывной в точке 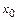 , то говорят, что в точке
, то говорят, что в точке 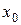 функция
функция 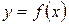 терпит разрыв, а точка
терпит разрыв, а точка 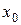 называется точкой разрыва функции.
называется точкой разрыва функции.
Разрыв функции 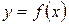 в точке
в точке 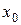 называется конечным, или первого рода, если существуют конечные односторонние пределы
называется конечным, или первого рода, если существуют конечные односторонние пределы 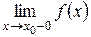 и
и 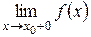 (при этом функция
(при этом функция 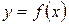 необязательно должна быть определена в точке
необязательно должна быть определена в точке 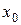 ).
).
Все другие случаи разрыва функции называются разрывами второго рода. В частности, если хотя бы один из односторонних пределов равен бесконечности, то и разрыв функции называется бесконечным.
Скачком функции 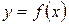 в точке разрыва
в точке разрыва 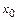 называется разность ее односторонних пределов, если они различны, т.е.
называется разность ее односторонних пределов, если они различны, т.е. 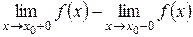 .
.
Если точка 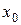 является левой или правой границей области определения функции
является левой или правой границей области определения функции 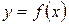 , то следует рассматривать значения функции соответственно только справа или только слева от этой точки и в самой этой точке.
, то следует рассматривать значения функции соответственно только справа или только слева от этой точки и в самой этой точке.
|
из
5.00
|
Обсуждение в статье: Следствия из второго замечательного предела |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

