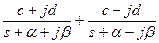|
Главная |
Пример 6. Определить передаточную функцию объекта регулирования, модель которого задана дифференциальным уравнением
|
из
5.00
|
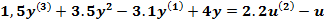
Введем в уравнение оператор Лапласа – s и вынесем yиu за скобки.
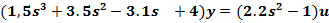
Делим многочлен правой части дифференциального уравнения на многочлен левой части, получаем выражение передаточной функции
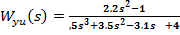 .
.
Задания для самостоятельного выполнения
Задание 1. Составить структурную схему по дифференциальному уравнению объекта и определить передаточную функцию (по примерам 5 и 6)
Варианты заданий:
| 1 | 3y(3) +6y(2) - 3y = u(2) - 2u(1) + u | 10 | 3y(3) +3y(2) + 2y(1) -y = - 4u(1) + u |
| 2 | y(3) - 3y(2) + 2y(1) + 5y = 3u(2) + u | 11 | 5y(3) - 5y = 3u(2) -2u(1) + u |
| 3 | -2y(3) + 4y(2) +2y(1) -5y = u(2) - 3u(1) + u | 12 | 4y(3) -3y(2) + 6y(1) + 2y = 3u(2) -2u(1) |
| 4 | 3y(3) - 4y(2) + 2y(1) =3u(2) - u(1) | 13 | 12y(3) + 4y(2) + 3y(1) + 2y = 3 u |
| 5 | 5y(3) - 7y(2) - 3y(1) = 2u(2) - u | 14 | 6y(3) - 4y(2) +-2y(1) = 6u(2) - 3u(1) + u |
| 6 | -3y(3) + 4y(2) + 6y(1) + 5y = -3 u | 15 | 8y(3) +3y(2) - 3y = -5u(2) - 3u(1) + u |
| 7 | 2y(3) - 4y(2) + 5y = - 3u(1) + u | 16 | 3y(3) + 3y(1) + 5y = 5u(2) +2u(1) + u |
| 8 | 6y(3) -+y(2) -y(1) = - 3u(1) + u | 17 | -4y(3) + 4y(2) -2y(1) + 7y = 5 u |
| 9 | - 4y(2) + 3y(1) + 5y = - 2u(1) + u | 18 | 3y(3) - 2y(2) - 3y(1) = u(2) - 4u(1) +2 u |
Задание 2
Преобразовать структурную схему и определить эквивалентную передаточную функцию. Варианты заданий приведены в таблице 1. (смотреть примеры 1-4)
Таблица 1.1. Варианты заданий по теме «Структурные схемы»
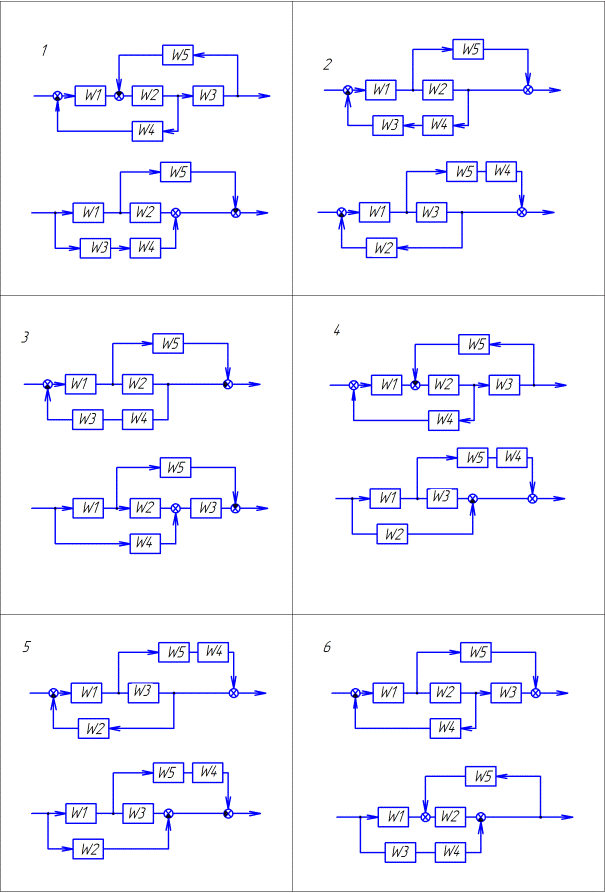
Продолжение таблицы 1.1. Варианты заданий
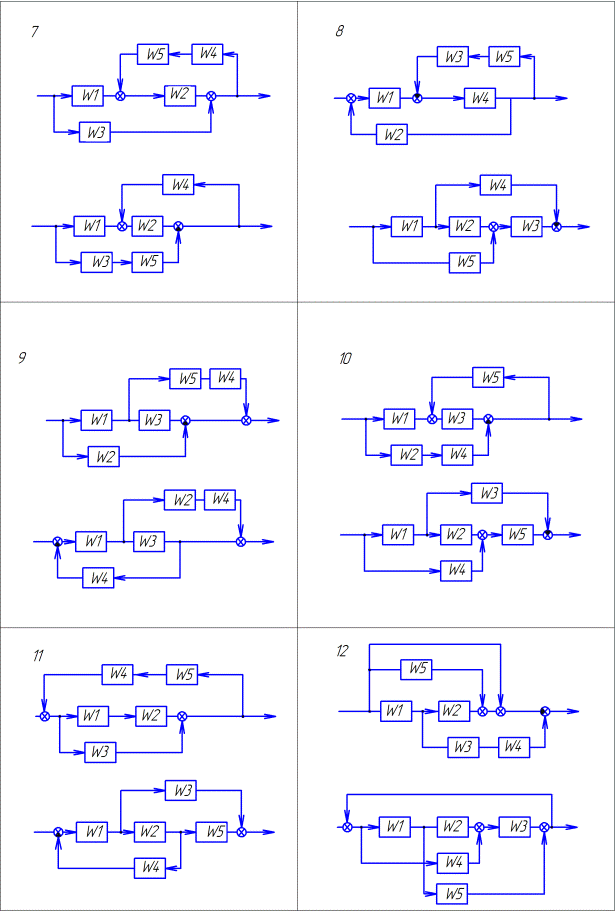
Продолжение таблицы 1.1. Варианты заданий
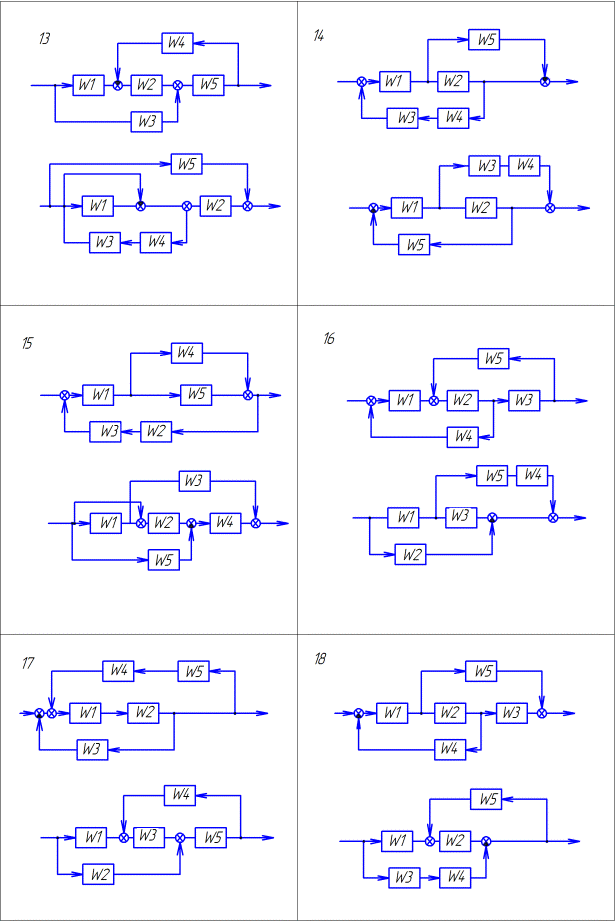
Продолжение таблицы 1.1. Варианты заданий 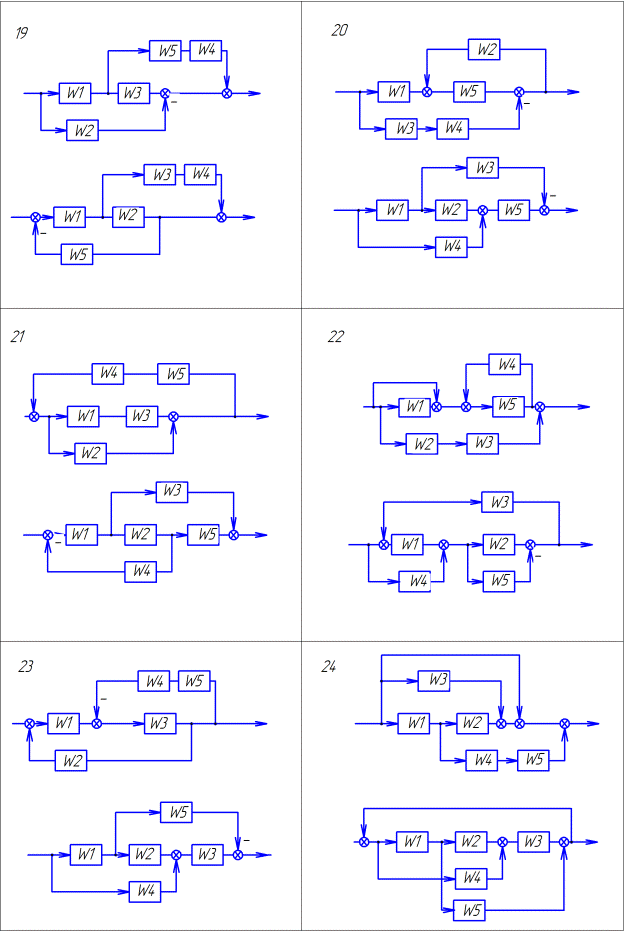
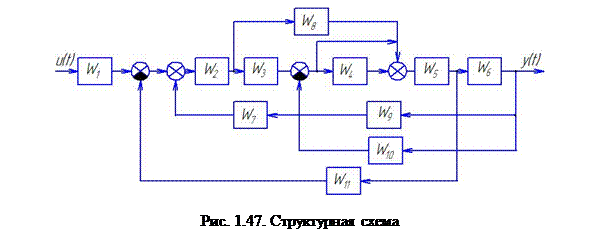
Задание 3. (без вариантов заданий, общее). Записать в общем виде главную передаточную функцию системы (рис. 1.47).
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА – теоретическая часть
Общие сведения
В ТАУ основным инженерным методом решения дифференциальных уравнений, т. е. исследования поведения систем во времени, является преобразование Лапласа. Его преимущество заключается в том, что операции дифференцирования и интегрирования оно заменяет более простыми алгебраическими операциями умножения и деления.
Рассмотрим принцип решения дифференциальных уравнений с помощью преобразования Лапласа.
1. На первом этапе производят прямое преобразование X ( s ) = L { x ( t )} – от функции времени переходят к функции комплексной переменной Лапласа s = σ + jω = α + jβ.
Здесь ω = 2π f – это известная из электротехники круговая частота, рад/с.
2. Далее решают алгебраическое уравнение реакции, для чего находят собственные значения системы, т. е. корни характеристического уравнения D ( s ) = 0, и по теореме разложения определяют коэффициенты числителей простых дробей, на которые в соответствии с собственными значениями разлагается реакция.
3. В конце вычислений выполняют обратное преобразование Лапласа x ( t ) = L -1 { X ( s )} – от функции переменной s возвращаются к функции переменной t.
Общее обозначение описанных операций x ( t )÷ X ( s ), где слева строчными буквами изображена функция времени (оригинал), справа, прописной буквой – функция комплексного переменного (изображение), а между ними стоит символ соответствия (ни в коем случае не равенства, что будет являться грубой ошибкой!).
Таблица 2. Таблица соответствия оригиналов и изображений
Изображение X(s) | Оригинал x(t) | |
| | импульсная функция k ∙δ(t) | |
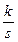
| – простой нулевой корень | скачок k∙1(t) или просто k |
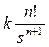
| – кратный нулевой корень | k ∙tn – степенной ряд от t |
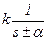
| – простой действительный корень | 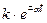 – экспонента – экспонента
|
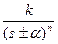
| – кратный действительный корень | 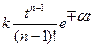 , при n > 1 , при n > 1
|
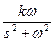
| – сопряженные мнимые корни | k∙sinωt – гармоническая функция |
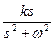
| – сопряженные мнимые корни | k∙cosωt – гармоническая функция |
| сопряженные комплексные корни
с вычислением | а) предпочтительная форма
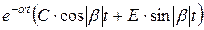 б) через синус
б) через синус
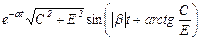 в) через косинус
в) через косинус
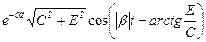
| |
| сопряженные комплексные корни (раздельное представление)
| 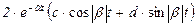 перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), и минус в противном случае
перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), и минус в противном случае
| |
Закон изменения выходного сигнала обычно является функцией, которую необходимо найти, а входной сигнал, как правило, известен.
Некоторые типовые входные и их изображения:
единичное ступенчатое воздействие имеет изображение X ( s ) = 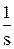 ,
,
дельта-функция X ( s ) = 1,
линейное воздействие X(s) = 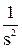 .
.
Пример. Решение ДУ с использованием преобразований Лапласа.
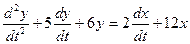
Допустим, входной сигнал имеет форму единичного ступенчатого воздействия, т.е. x(t) = 1. Тогда изображение входного сигнала, согласно таблице 2, имеет вид X(s) = 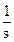 .
.
Производим преобразование исходного ДУ по Лапласу и подставляем X(s):
s2×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s×X(s) + 12×X(s),
s2×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s 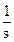 + 12
+ 12 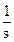 ,
,
Y(s)×(s3 + 5s2 + 6s) = 2×s + 12.
Определяется выражение для Y:
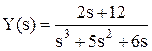 .
.
Оригинал полученной функции отсутствует в таблице оригиналов и изображений. Для решения задачи его поиска дробь разбивается на сумму простых дробей с учетом того, что знаменатель может быть представлен в виде s ( s + 2)( s + 3):
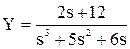 =
= 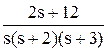 =
= 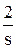 -
- 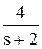 +
+ 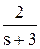 .
.
Теперь, используя табличные функции (см. табл. 2), определяется оригинал выходной функции:
y(t) = 2 - 4.e-2t + 2.e-3t.
При решении ДУ с использованием преобразований Лапласа часто встает промежуточная задача разбиения дроби на сумму простых дробей. Существуют два пути решения этой задачи:
- путем решения системы уравнений относительно коэффициентов числителей,
- путем расчета коэффициентов числителей по известным формулам.
Общий алгоритм разбиения дроби на сумму простых дробей:
шаг 1 – определяются корни знаменателя si (знаменатель дроби приравнивается к нулю и решается полученное уравнение относительно s);
шаг 2 – каждому корню ставится в соответствие простая дробь вида 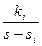 , где М i – неизвестный коэффициент; если имеет место кратный корень с кратностью n , то ему ставится в соответствие n дробей вида
, где М i – неизвестный коэффициент; если имеет место кратный корень с кратностью n , то ему ставится в соответствие n дробей вида 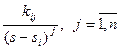 ;
;
шаг 3 – определяются коэффициенты ki по одному из вариантов расчета.
Продолжение метода:
|
из
5.00
|
Обсуждение в статье: Пример 6. Определить передаточную функцию объекта регулирования, модель которого задана дифференциальным уравнением |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


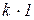
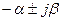 , объединенные в одну дробь
, объединенные в одну дробь 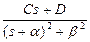 ,
,