Столкновение шарика со стенкой

2015-11-08

1321

Обсуждений (0)

0.00 из 5.00 0 оценок

Класс

Задача 1. Горючая смесь.
Найдите отношение масс спирта и бензина в смеси, удельная теплота сгорания которой q_o= 41 МДж/кг. Удельная теплота сгорания бензина q_b= 44 МДж/кг, а удельная теплота сгорания спирта q_c= = 26 МДж/кг.

Задача 2. Электрички.
Две электрички, длинной L = 200 м каждая, движутся навстречу друг другу по параллельным железнодорожным путям. Скорость электричек отличается на Δv = 40 км/ч. Расстояние между встречей первых и последних вагонов равно d = 40 м. Определить скорость электричек.

Задача 3. Шнур и зажигалка.
Имеются два неоднородных шнура и зажигалка. Если поджечь любой из шнуров, то он полностью сгорит за час. Как нужно действовать, чтобы таким способом отмерить 45 минут. Резать и рвать шнуры нельзя.

Задача 4. Блоки.
Для постоянного натяжения линии трамвайного провода используется следующая система простых механизмов изображенных на рисунке. Конец провода прикреплен к столбу. Масса подвешенного груза равна 100 кг. Опорный столб, к которому крепится система простых механизмов, стоит в цилиндрическом колодце. Найдите силы, которые действуют на столб в точках A и B. Высота столба H = 10 м, глубина погружения столба в цилиндрический стакан h = 1,5 м. [решение]

Задача 5. Теплообмен.
В железном калориметре массой 100 г находится 0,5 кг воды при температуре 15 °C. В калориметр бросают свинец и алюминий общей массой 150 ги температурой 100 °C. В результате температура воды поднялась до 17 °С. Определите массы алюминия и свинца. Удельная теплоемкость свинца126 Дж/(кг•°C), алюминия 836 Дж/(кг•°C), железа 460 Дж/(кг•°C), воды 4200 Дж/(кг•°C). Тепловыми потерями в системе пренебречь.

Решения

Задача 1. Горючая смесь.
Найдите отношение масс спирта и бензина в смеси, удельная теплота сгорания которой q_o= 41 МДж/кг. Удельная теплота сгорания бензина q_b= 44 МДж/кг, а удельная теплота сгорания спирта q_s= = 26 МДж/кг.

Решение.
Пусть в смеси находится масса т_b бензина и масса m_s спирта. Тогда, с одной стороны, теплота сгорания смеси

Q = q_b× m_b+ q_s× m_s (1)

с другой стороны,

Q = q_o× (m_b+ m_s. (2)

Из (1) и (2) получим

q_b× m_b+ q_s× m_s= q_o× (m_b+ m_s,

откуда находим искомое отношение:

m_b/m_s= (q_o− q_s)/(q_b− q_o) = 5.

Таким образом, массы бензина и спирта находятся в смеси в отношении 5:1.

Задача 2. Электрички.
Две электрички, длинной L = 200 м каждая, движутся навстречу друг другу по параллельным железнодорожным путям. Скорость электричек отличается на Δv = 40 км/ч. Расстояние между встречей первых и последних вагонов равно d = 40 м. Определить скорость электричек.

Решение.
Если бы электрички имели одинаковую скорость, то точка встречи первых вагонов и точка расхождения последних вагонов совпала.
Обозначим Δt – промежуток времени от начала встречи первых вагонов и расхождения последних. Пусть также скорость первой электрички больше второй, тогда она за время Δt пройдет расстояние большее и отстоящее от точки встречи первых вагонов на 40 м. Очевидно, что за время Δt, первая электричка проходит расстояние L + d, а вторая – L − d. Время движения электричек

Δt = (L + d)/v₁

Δt = (L − d)/v₂

Приравняем время

(L + d)/v₁= (L − d)/v₂.

Откуда

v₂= v₁(L − d)/(L + d) = (v₂+ Δv)(L − d)/(L + d).

После преобразований

v₂= Δv(L − d)/(2d).

или

v₂= 40 × (200 − 40)/(2 × 40) = 80 км/ч, а v₁= 120 км/ч.

Так как в условии задачи не оговорено, какая электричка имеет большую скорость, то может быть и симметричный ответ

v₁= 80 км/ч, а v₂= 120 км/ч.

Задача 3. Шнур и зажигалка.
Имеются два неоднородных шнура и зажигалка. Если поджечь любой из шнуров, то он полностью сгорит за час. Как нужно действовать, чтобы таким способом отмерить 45 минут. Резать и рвать шнуры нельзя.

Решение.
Если мы первый шнур сложим пополам и подожжем в середине, то шнур сгорит за полчаса.
Значит, надо сложить первый шнур пополам и соединить со вторым шнуром сложенным вчетверо.

60 мин/2 + 60 мин/4 = 30 мин + 15 мин = 45 мин.

Задача 4. Блоки.
Для постоянного натяжения линии трамвайного провода используется следующая система простых механизмов изображенных на рисунке. Конец провода прикреплен к столбу. Масса подвешенного груза равна 100 кг. Опорный столб, к которому крепится система простых механизмов, стоит в цилиндрическом колодце. Найдите силы, которые действуют на столб в точках A и B. Высота столба H = 10 м, глубина погружения столба в цилиндрический стакан h = 1,5 м.

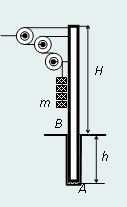
Решение.
Провод в трамвайной линии натянут с силой F = 3920 H.
На нижний блок действует со стороны подвешенного груза сила

980 Н.

На средний блок, со стороны троса действует сила

1960 Н.

На первый блок действует сила

3920 Н.

Здесь принято g = 9,8 H/кг.
Столб как рычаг. Справедливо правило моментов

F × H = F_A× h,

F × (H + h) = F_B× h.

Получим

F_A= F × H/h = 26130 H,

F_B= F × (H + h)/h = 30050 H.

Решение:
Запишем уравнение теплового баланса в системе «калориметр с водой + куски алюминия и свинца»:

Q₁= Q₂, (1)

где

Q₁= c_жm_ж(t₂- t₁) + c_вm_в(t₂- t₁)

– количество теплоты, полученное калориметром с водой;

Q₂= c_am_a(t - t₂) + c_cm_c(t - t₂)

– количество теплоты, отдаваемое кусками алюминия и свинца. Согласно условию задачи

m_a+ m_c= m, (2)

где m = 0,15 кг.
Подставляя в формулу (1) Q₁ и Q₂ с учетом (2), а так же считая, что

t₁= 15 °C, t₂= 17 °C, t = 100 °C,

получим

m_a= (c_жm_ж+ c_вm_в)(t₂− t₁)/{(c_a− c_c)(t − t₂)} − c_cm/(c_a− c_c);

m_c= c_am/(c_a− c_c) − (c_жm_ж+ c_вm_в)(t₂− t₁)/{(c_a− c_c)(t − t₂)}.

После вычислений m_a= 0,046 кг, m_c= 0,104 кг.

9 класс

1. Веловстречи.
Два велосипедиста одновременно выехали из пунктов А и В навстречу друг другу и встретились через 1 час. После встречи они продолжили свое движение в прежнем направлении. Доехав до пунктов В и А соответственно, они сразу развернулись и поехали обратно. Через какое время, после первой встречи, они опять поравняются друг с другом. [решение]

2. Не идеальный вольтметр.
В цепи, изображенной на рисунке, вольтметр измеряет падение напряжения на резисторе сопротивлением R = 300 кОм. Каким может быть сопротивление вольтметра для того чтобы его показания отличались не больше чем на 2 % от допустимого значения U_o. Сопротивление R₁ = 100 кОм. [решение]

3. 48 ложек воды.
В калориметр вливают ложку горячей воды, при этом его температура возросла на 5 °С. После этого в него влили опять ложку горячей воды и температура поднялась еще на 3 °С. На сколько градусов возрастет температура калориметра, если в него влить еще 48 ложек горячей воды. Теплообменом с окружающей средой пренебречь. [решение]

4. Неравноплечий рычаг.
Два тела разных плотностей и объемов подвесили на нитях к краям невесомого стержня, причем равновесие стержня достигается, если его подпереть так, что расстояния от точки опоры до тел отличается в два раза. После того как тела полностью погрузили в воду, для сохранения равновесия стержня пришлось поменять местами тела. Найдите плотности тел, если известно, что их плотности отличаются в 2,5 раза. Плотность воды считать известной ρ_о. [решение]

5. Сообщающийся сосуд.
В сообщающийся сосуд (см. рисунок) налита вода. В левый сосуд налили керосин высотой H₁ = 20 см, а в правый − высотой H₂ = 1,25H₁. На сколько повысился уровень воды в среднем сосуде? Известно, что ρ_в/ρ_к = 1,25. [решение]

Класс

Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы (1 балл)

Расстояние между пунктами А и В обозначим как сумму АС + CВ

L = x₁ + x₂. (2 балла)

Время до первой встречи найдем перейдя в систему отсчета, связанную с одним из велосипедистов

t = L/(v₁ + v₂). (2 балла)

После первой встречи велосипедисты разъехались, доехав до конечных пунктов, развернулись и вновь встретились в п. D. При этом они проехали расстояние до встречи

x₂ + x₄ + x₁ + x₃ = L + L = 2L. (2 балла)

Время до новой встречи

t₁ = 2L/(v₁ + v₂) = 2t. (2 балла)

После первой встречи велосипедисты встретятся через 2 ч. (1 балл)
Всего за задачу 10 баллов

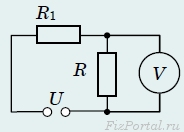
Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы (1 балл)
При отсутствии вольтметра сопротивления R и R₁ соединены последовательно, поэтому падение напряжения на сопротивлении R равно

U_R = IR = UR/(R + R₁). (2 балла)

При подключении вольтметра он измеряет напряжение на участке, который состоит и з параллельно соединенных резистора, сопротивлением R и сопротивления вольтметра R_V.
В этом случае ток в цепи

I = U/(R₁ + RR_V/(R + R_V)) (1 балл)

Показание вольтметра

U_R^/ = U/(R₁ + RR_V/(R + R_V)) × RR_V/(R + R_V) = URR_V/(R₁R + R₁R_V + RR_V). (2 балла)

По условию задачи показания вольтметра не должны превышать 2 %

(U_R − U_R^/)/U_R ≤ 0,02, (2 балла)

или

1 − R_V(R + R₁)/(R₁R + R₁R_V + RR_V) ≤ 0,02. (1 балл)

Решая последнее неравенство относительно искомого сопротивления вольтметра, получим

R_V ≤ 49 × RR₁/(R + R₁) ≤ 3675 кОм. (1 балл)

Решение.
Приступил к решению задачи, записал основные формулы (1 балл)
Обозначим С_к − теплоемкость калориметра, С_в − теплоемкость одной ложки воды, t_в − температура горячей воды и t_o − начальная температура калориметра.
Запишем уравнение теплового баланса после вливания одной ложки

С_к(t_o + 5 − t_o) = C_в(t_в − (t_o + 5)), (1) (2 балла)

После вливания второй ложки

С_к(t_o + 8 − t_o) = 2C_в(t_в − (t_o + 8)), (2) (2 балла)

Разделим второе уравнение на первое

(t_в − t_o − 8)/(t_в − t_o − 5) = 4/5.

Откуда t_в − t_o = 20. (1 балл)
Из уравнения теплового баланса (1)

5C_к = 15С_в и C_к = 3С_в. (1 балл)

После вливания еще 48 ложек горячей воды

С_к(t_к − t_o) = 50C_в(t_в − t_к), (1 балл)

Откуда

53t_к = 50t_в + 3t_o = 53t_в − 3(t_в − t_o) или t_к = t_в − (3/53) × (t_в − t_o). (1 балл)

Искомая разность температур

t_к − t_o = t_в − t_o − (3/53) × (t_в − t_o) = (50/53) × (t_в − to) ≈ 18,9 °C. (1 балл)

Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы (1 балл)
Запишем условие равновесия стержня до погружения в воду

ρ₁V₁ = 2ρ₂V₂, (1) (2 балла)

после погружения в воду

2(ρ₁ − ρ_o)V₁ = (ρ₂ − ρ_o)V₂. (2) (2 балла)

Выразим из (1) V₁/V₂ = 5 (2 балла)
и подставим в (2)

10ρ₁ − ρ₂ = 9ρ_o. (2 балла)

Решая это уравнение совместно с условием задачи ρ₂/ρ₁ = 2,5, находим

ρ₁ = 1,2ρ_o и ρ₂ = 3ρ_o. (1 балл)

Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы (1 балл)
Предположим, что в левом сосуде уровень воды понизился на h₁, а в правом понизился на h₂. Тогда в среднем сосуде уровень воды повысится наh₁ + h₂ и будет выше, чем в правом сосуде на h₁ + 2h₂ и выше, чем в левом сосуде на 2h₁ + h₂. (2 балла)
Так как жидкость находится в равновесии, то давление столбов воды равно давлению столбов керосина:

ρ_вg(2h₂ + h₁) = ρ_кgH₂, ρ_вg(2h₁ + h₂) = ρ_кgH₁, (1) (2 балла)

где ρ_в − плотность воды, ρ_к − плотность керосина
Перепишем уравнения (1)

2h₂ + h₁ = (ρ_к/ρ_в) × H₂, 2h₁ + h₂ = (ρ_к/ρ_в) × H₁.

или

2h₂ + h₁ = 0,8H₂, 2h₁ + h₂ = 0,8H₁,

(2h₂ + h₁)/(2h₁ + h₂) = 1,25.

Откуда h₂ = 2h₁. (2 балла)

2 × 2h₁ + h₁ = 0,8H₂, h₁ = 0,8H₂/5 = 4 см, h₂ = 2h₁ = 8 см. (2 балла)

Откуда h₁ + h₂ = 4 см + 8 см = 12 см. (1 балл)

Класс

1. Тянем потянем.
В горизонтально закрепленной, открытой с торцов трубе сечением S находятся два поршня. В исходном состоянии левый поршень соединен недеформированной пружиной жесткости k со стенкой, давление газа между поршнями равно атмосферному p_o, расстояние H от правого поршня до края трубы равно расстоянию между поршнями. Правый поршень медленно вытянули до края трубы. Какую минимальную силу надо приложить к поршню, чтобы удержать его в этом положении? Температура постоянна, трением пренебречь. [решение]

2. Испытание ракеты.
С края полусферической выемки радиуса R отпускают из состояния покоя тело, состоящее из двух половинок с пороховым зарядом между ними. Если взорвать заряд в начальный момент на краю выемки, то обе половинки взлетают на одинаковую высоту h. На какие высоты h₁ и h₂ поднялись бы эти половинки, если заряд взорвать в момент прохождения нижней точки выемки? При каком условии левая половинка, после взрыва в нижней точке, не вылетит из выемки. Трением и сопротивлением воздуха пренебречь. [решение]

3. На лабораторной работе.
Выполняя лабораторную работу, юный физик собрал схему (см. рисунок). Когда вольтметр был подключен параллельно сопротивлению R₁, то его показания оказались равны U₁ = 2 B, после подключения вольтметра параллельно сопротивлению R₂, его показания U₂ = 1 B, а после подключения к точкам A и B, он показал U = 4 B. Что-то не сходится, подумал юный физик и задумался. А каковы в действительности падения напряжения на сопротивлениях R₁ и R₂? В качестве источника использовалась батарейка. И еще учитель сказал, что источник можно считать идеальным и его внутренним сопротивлением пренебречь. [решение]

4. Супер чайник.
При испытании новой модели электрического чайника (рис.) оказалось, что вода нагревается почти до 100 °С, но все же не закипает. Чайник рассчитан на мощность нагревателя P и напряжение 110 В. Тогда чайник подключили к сети 220 В. За какое время чайник выкипит наполовину? Масса воды в чайнике m. Удельная теплота парообразования воды L. Крышка чайника плотно закрывается. Чайник изготовлен из металла. [решение]

5. Столкновение шарика со стенкой.
Маленький шарик, брошенный с начальной скоростью v_о под углом α к горизонту, упруго ударяется о гладкую вертикальную стенку, движущуюся ему навстречу с постоянной скоростью v. Известно, что после упругого удара о стенку шарик возвращается в ту точку, из которой его бросили. Через какое время после броска произошло столкновение шарика со стенкой? [решение]

Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы (1 балл)

Запишем условие равновесия левого поршня

p_oS − kx − p₁S. (1) (1 балл)

Условие равновесия правого поршня:

p₁S + F − p_oS = 0. (2) (1 балл)

Применим закон Бойля-Мариотта

p_oH = p₁(2H − x). (3) (1 балл)

Из уравнений (1) и (2) следует, что

F = kx, т.е. x = F/k. (1 балл)

Из уравнения (2)

p₁ = p_o − F/S. (1 балл)

Из уравнения (3)

p_oH = (p_o − F/S) × (2H − F/k).

Таким образом, получаем квадратное уравнение

F² − F(2kH + p_oS) + p_oHkS = 0. 2 балла

F₁₂ = (2kH + p_oS ± √{(2kH + p_o)² − 4p_oHkS})/2.

F₁₂ = kH + p_oS/2 ± √{(kH)² + (p_oS/2)²}. (1 балл)

При k → 0, F → 0, окончательно получаем

F = kH + p_oS/2 − √{(kH)² + (p_oS/2)2}. (1 балл)

Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы (1 балл)
В первом случае, когда заряд взрывается на краю выемки энергия взрыва идет на сообщение телам потенциальной энергии. Скорость, которую сообщает половинке энергия взрыва

E = mv²/2 = mgh. (1 балл)

Следовательно, при взрыве заряда половинка тела приобретает скорость

v² = 2gh. (1) (1 балл)

Во втором случае, в нижней точке выемки тело имеет кинетическую энергию

mu²/2 = mgR, (1 балл)

и, следовательно, перед разрывом заряда, скорость

u² = 2gR. (2) (1 балл)

Правая половинка, в результате энергии взрыва получит дополнительную скорость u + v, а левая половинка v − u. (1 балл)
Кинетическая энергия правой (левой) половинки равна потенциальной энергии относительно нижней точки разрыва

m(v + u)²/2 = mg(R + h₁), m(v − u)²/2 = mg(R + h₂) (1 балл)

Откуда

h₁ = (v + u)²/(2g) − R и h₂ = (v − u)²/(2g) − R. (3) (1 балл)

Сделаем подстановку (1) и (2) в (3)

h₁₂ = h ± 2√{Rh}. (1 балл)

Приравняем к нулю уравнение

h₂ = h − 2√{Rh} = 0, откуда h = 4R. (1 балл)

Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы (1 балл)
При подключении вольтметра к точкам A и B его показание равно ЭДС источника. Поэтому если вольтметр подключен к сопротивлению R₁, а внутреннее сопротивление вольтметра R, то по цепи идет ток

I = U/(R₂ + R₁R/(R₁ + R)). (1 балл)

Это означает, что

U₁ = U/(R₂ + R₁R/(R₁ + R)) × R₁R/(R₁ + R). (1) (2 балла)

Точно так же

U₂ = U/(R₁ + R₂R/(R₂ + R)) × R₂R/(R₂ + R). (2) (2 балла)

Разделив конечное уравнение (1) на уравнение (2), получим

U₁/U₂ = R₁/R₂.

Таким образом, R₁/R₂ = 2/1 = 2. (1 балл)
При отключенном вольтметре падение напряжения на сопротивлениях R₁ и R₂ равно U = 4 B. Так как отношение сопротивлений известно, нетрудно найти и падения напряжения U₁^/, U₂^/ на сопротивлениях:

U₁^/ + U₂^/ = U, U₁^//U₂^/ = R₁/R₂. 1 балл

Отсюда

U₁^/ = UR₁/(R₁ + R₂) = U/(1 + R₂/R₁) = 2,66 B; U₂^/ = U − U₁^/ = 1,33 B. (2 балла)

Решение.
Приступил к решению задачи, записал основные формулы. (1 балл)
Теплообмен чайника со средой определяется температурой поверхности чайника. При нагревании чайника до 100 °С вся подводимая энергия нагревателя отводится в окружающую среду. И в первом и во втором случае мощность тепловых потерь одинакова и равна P. (1 балл)
При включении в сеть с напряжением 220 В мощность нагревателя

P₂/P = (U₂²/R) × (R/U²) = 4 и P₂ = 4P. (2 балла)

Тогда для второго случая

4P = P + Q_пар/t и Q_пар = 3Pt. (2 балла)

Где

Q_пар = Lm/2. (2 балла)

Тогда

3Pt = Lm/2. (1 балл)

Отсюда

t = Lm/(6P). (1 балл)

Столкновение шарика со стенкой.

Маленький шарик, брошенный с начальной скоростью v_о под углом α к горизонту, упруго ударяется о гладкую вертикальную стенку, движущуюся ему навстречу с постоянной скоростью v. Известно, что после упругого удара о стенку шарик возвращается в ту точку, из которой его бросили. Через какое время после броска произошло столкновение шарика со стенкой?

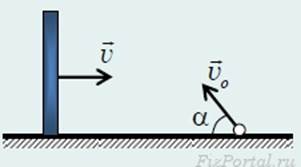
Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы. (1 балл)
Пусть горизонтальная и вертикальная составляющие скорости шарика при подлете к стенке равны v₁ и v₂ (см. рисунок).

Так как стенка гладкая, вертикальная составляющая скорости шарика в момент удара о стенку не изменится. А поскольку полное время движения тела, брошенного под углом к горизонту, определяется вертикальной проекцией скорости, то время движения t будет таким же, как и в отсутствие стенки (1 балл)

t = 2v_osinα/g. (1) (1 балл)

Чтобы найти, как меняется горизонтальная проекция скорости шарика при ударе, перейдем в систему отсчета, связанную со стенкой. В этой системе отсчета горизонтальная проекция скорости шарика до удара равна v₁ + v. А поскольку масса стенки гораздо больше массы шарика, то его горизонтальная скорость в этой системе отсчета изменится на противоположную. Поэтому в системе отсчета, связанной с землей, горизонтальная составляющая скорости шарика будет направлена от стенки и равна по величине v₁ + 2v. (2 балла)
А поскольку горизонтальная проекция скорости шарика равна v_ocosα, то

v₁ + 2v = v_ocosα + 2v. (2) (1 балл)

Учтем теперь, что шарик упал в ту же точку, откуда начал движение. Пусть t₁ ? время движения шарика до столкновения со стенкой. Тогда до столкновения шарик прошел расстояние

l₁ = v_ocosα × t₁. 1 балл

Расстояние, пройденное шариком после столкновения, определяется горизонтальной проекцией скорости после столкновения и временем от момента столкновения до падения, или с учетом формулы (2)

l₂ = (v_ocosα + 2v)(t − t₁). (1 балл)

А поскольку шарик упал в ту же точку, то l₁ = l₂:

v_ocosα × t₁ = (v_ocosα + 2v)(t − t₁). (3) 1 балл

Решая уравнение (3) относительно времени t₁ и используя (1), находим

t₁ = v_osinα(v_ocosα + 2v)/(g(v_ocosα + v)). 1 балл

11 класс

1. Поршни в длинной трубе.
В горизонтальной достаточно длинной трубе между двумя поршнями находится моль идеального одноатомного газа. В остальных частях трубы создан вакуум. В некоторый момент времени абсолютная температура газа равна T_o, а поршни движутся навстречу друг другу со скоростями модули которых равны v₁ и v₂. Найдите температуру газа в тот момент, когда его давление станет максимальным. Масса каждого поршня равна M и значительно больше массы газа.
Допущения: процесс сжатия считайте равновесным, теплообменом газа с окружающими телами пренебречь. [решение]

2. Испытание пружинной пушки.
Ствол пружинной пушки направлен под углом 45° к гладкому полу. Масса снаряда равна массе пушки. Определите отношение высот подъема снаряда при выстрелах из незакрепленной и закрепленной пушки. [решение]

3. Два вольтметра.
Два вольтметра с внутренним сопротивлениями R₁ и R₂ = 2R₁ соединены так, как показано на рисунке. Сопротивлением R₃ = 4R₁, напряжение U = 6 B. Определить показание вольтметров при разомкнутом и при замкнутом ключе К и установке движка D на середине сопротивления R₃. Где будет расположен движок на сопротивлении R₃, при одинаковых показаниях вольтметров? [решение]

4. Частица в магнитном поле.
Частица массой m заряда +q в начале координат имеет скорость V направленную вдоль оси z. Выше плоскости z = 0 имеется постоянное магнитное поле B_x, направленное вдоль оси x. Ниже плоскости z = 0 магнитное поле постоянно, равно B_y и направлено вдоль оси y. Определите, координаты точки, где частица пересечет плоскость z = 0 в 3-й раз. Изобразите траекторию частицы. [решение]

5. Шайба на транспортере.
Лента транспортера натянута горизонтально и движется с постоянной скоростью u. Навстречу движению ленты со скоростью v пускают скользить шайбу, которая удаляется от точки пуска на максимальное расстояние l. Через какое время шайба вернется в точку пуска? [решение]

Решение.
Первое решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы (1 балл)
Запишем закон сохранения энергии

(3/2)RT_o + Mv₁²/2 + Mv₂²/2 = (3/2)RT + Mv²/2 + Mv²/2. (2 балла)

где, применив закон сохранения импульса в проекции на направление движения первого поршня

mv₁ − mv₂ = mv + mv (2 балла)

v = (v₁ − v₂)/2. (1 балл)

Давление будет максимальным, когда объем станет минимальным.

Поршни движутся навстречу друг другу, затем тот поршень у которого импульс меньше остановится и изменит направление движения на противоположное. До тех пор пока скорости поршней не сравняются, объем между поршнями будет уменьшаться. (2 балла)
При замене скорости в уравнении энергии, получим такой же конечный ответ

T = T_o + M(v₁ + v₂)²/(6R). (2 балла)

Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы. (1 балл)
Пусть скорость пушки после выстрела − V, горизонтальная скорость снаряда − v, вертикальная − u.
Если пушка не закреплена, то по закону сохранения импульса

mV = mv, (1 балл)

так как масса пушки и снаряда равны, то

V = v. (1 балл)

Относительно пола

V + v = u, (1 балл)

так как угол наклона пушки 45° и относительно нее горизонтальная составляющая скорости равна вертикальной, таким образом,

u = 2V. 1 балл

Для закрепленной пушки имеем однозначно

v^/ = u^/ (1 балла)

подчеркнем, что u^/ ≠ u.
Энергия сжатой пружины в обоих случаях одинакова, поэтому из закона сохранения энергии имеем

m(v² + u²)/2 + mV²/2 = mv^/2/2 + mu^/2/2. (2 балла)

Подставляя

u² = 4V², v² = V² и v^/2 = u^/2,

получаем

u^/2 = 3V². (1 балл)

Так как высота подъема снаряда h = u²/(2g), то для отношения высот получаем

h/h^/ = (u/u^/)² = 4/3. (1 балл)

Решение.
Приступил к решению задачи, выполнил рисунок, записал основные формулы. (1 балл)
При разомкнутом ключе напряжение на вольтметрах равно U, а ток через них

I = U/(R₁ + R₂). (1 балл)

Показание вольтметров равно

U₁ = IR₁ = UR₁/(R₁ + R₂); U₂ = IR₂ = UR₂/(R₁ + R₂). (1 балл)

После замены R₁, R₂ = 2R₁, R₃ = 4R₁, получим

U₁ = 2 B, U₂ = 4 B. 1 балл

2. При замкнутом ключе К и установке движка D на середине сопротивления R₃ рассмотрим эквивалентную схему

Столкновение шарика со стенкой

Обсуждение в статье: Столкновение шарика со стенкой