 |
Главная |
Транспонирование матриц
|
из
5.00
|
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
1. Действия над матрицами.
Матрицей называется прямоугольная таблица элементов, например

Размерность матрицы обозначают  , где
, где 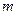 - число строк, а
- число строк, а  - число столбцов матрицы. Например, размерность матрицы А -
- число столбцов матрицы. Например, размерность матрицы А -  , матрицы В -
, матрицы В -  ,
,
матрицы  -
-  . В общем случае элемент матрицы обозначают
. В общем случае элемент матрицы обозначают  , где
, где  - номер строки, а
- номер строки, а  - номер столбца матрицы, на пересечении которых находится этот элемент. Например, для матрицы А
- номер столбца матрицы, на пересечении которых находится этот элемент. Например, для матрицы А  , для матрицы В
, для матрицы В  .
.
Определим действия над матрицами.
Умножение матрицы на число и сложение покажем на примерах.
Умножение матрицы на число.
Пример.
 или
или 
Сложение (вычитание) матриц.
Пример.

3.Умножение матриц.
Если матрица А имеет размерность  , а матрица В имеет размерность
, а матрица В имеет размерность  , то их можно умножать. В результате получается матрица
, то их можно умножать. В результате получается матрица  , размерность которой будет
, размерность которой будет  . Например,
. Например,  размерности
размерности  , В размерности
, В размерности  , то
, то  будет размерности
будет размерности  .
.
Пример.

Первую строку А умножаем на первый столбец В:  .
.
Первую строку А умножаем на второй столбец В:  .
.
Вторую строку А умножаем на первый столбец В:  .
.
Вторую строку А умножаем на второй столбец В:  .
.
Пример.

Пример.

Транспонирование матриц.
Чтобы транспонировать матрицу, надо строки матрицы записать в столбцы.
Пример.
Если  , то транспонированная матрица
, то транспонированная матрица 
Если 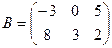 , то
, то 
Задание 1.Найти 

Решение.

- Определители квадратных матриц.
Для квадратных матриц вводится число, которое называется определителем.
Для матриц второго порядка ( размерность  ) определитель задается формулой:
) определитель задается формулой:

Например, для матрицы  ее определитель
ее определитель 
Пример.Вычислить определители матриц.
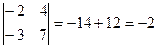


Для квадратных матриц третьего порядка (размерность  ) существует правило «треугольника»: на рисунке пунктирная линия означает – умножить числа, через которые проходит пунктирная линия. Первые три числа надо сложить, следующие три числа надо вычитать.
) существует правило «треугольника»: на рисунке пунктирная линия означает – умножить числа, через которые проходит пунктирная линия. Первые три числа надо сложить, следующие три числа надо вычитать.

Пример. Вычислить определитель.



Чтобы дать общее определение определителя, надо ввести понятие минора и алгебраического дополнения.
Минором  элемента матрицы
элемента матрицы  называется определитель, полученный вычеркиванием
называется определитель, полученный вычеркиванием  - той строки и
- той строки и  - того столбца.
- того столбца.
Пример. Найдем некоторые миноры матрицы А.






Алгебраическим дополнением  элемента
элемента  называется число
называется число  .
.
Значит, если сумма индексов  и
и  четная, то
четная, то  и
и  ничем не отличаются. Если же сумма индексов
ничем не отличаются. Если же сумма индексов  и
и  нечетная, то
нечетная, то  и
и  отличаются только знаком.
отличаются только знаком.
Для предыдущего примера  .
.
Определителем матрицыназывается сумма произведений элементов некоторой строки
( столбца) на их алгебраические дополнения. Рассмотрим это определение на матрице третьего порядка.
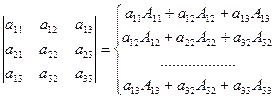
Первая запись называется разложением определителя по первой строке, вторая - разложение по второму столбцу, последняя – разложение по третьей строке. Всего таких разложений можно записать шесть раз.
Пример. Вычислить определитель по правилу «треугольника» и разложив его по первой строке, затем по третьему столбцу, затем по второй строке.

Разложим определитель по первой строке:

Разложим определитель по третьему столбцу:
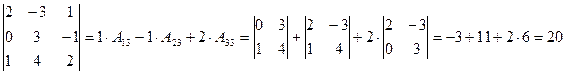
Разложим определитель по второй строке:

Заметим, что чем больше нулей, тем проще вычисления. Например, раскладывая по первому столбцу, получим

Среди свойств определителей есть свойство, позволяющее получать нули, а именно:
Если к элементам некоторой строки (столбца) прибавить элементы другой строки (столбца), умноженные на ненулевое число, то определитель не изменится.
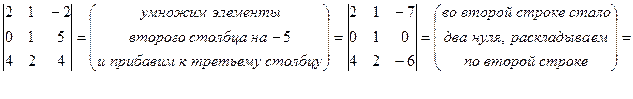
 .
.
Возьмем этот же определитель и получим нули, например, в первой строке.
 =
= 
Определители более высоких порядков вычисляются таким же образом.
Задание 2.Вычислить определитель четвертого порядка:
1) разложив по любой строке или любому столбцу
2) получив предварительно нули


Получим дополнительный ноль, например, во втором столбце. Для этого элементы второй строки умножим на -1 и прибавим к четвертой строке:

- Решение систем линейных алгебраических уравнений методом Крамера.
Покажем решение системы линейных алгебраических уравнений методом Крамера.
Задание 2. Решить систему уравнений.

Надо вычислить четыре определителя. Первый называется основным и состоит из коэффициентов при неизвестных:

Заметим, что если 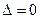 , систему методом Крамера решить нельзя.
, систему методом Крамера решить нельзя.
Три остальных определителя обозначаются  ,
,  ,
,  и получаются заменой соответствующего столбца на столбец правых частей.
и получаются заменой соответствующего столбца на столбец правых частей.
Находим  . Для этого первый столбец в основном определителе меняем на столбец правых частей:
. Для этого первый столбец в основном определителе меняем на столбец правых частей:

Находим  . Для этого второй столбец в основном определителе меняем на столбец правых частей:
. Для этого второй столбец в основном определителе меняем на столбец правых частей:
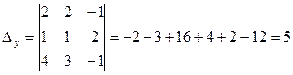
Находим  . Для этого третий столбец в основном определителе меняем на столбец правых частей:
. Для этого третий столбец в основном определителе меняем на столбец правых частей:
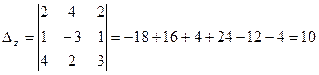
Решение системы находим по формулам Крамера: 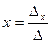 ,
,  ,
, 
 ,
,  ,
, 
Таким образом решение системы  ,
,  ,
, 
Сделаем проверку, для этого найденное решение подставим во все уравнения системы.

- Решение систем линейных алгебраических уравнений матричным методом.
Если у квадратной матрицы  определитель не равен нулю, существует обратная матрица
определитель не равен нулю, существует обратная матрица  , такая что
, такая что 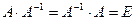 . Матрица
. Матрица  называется единичной и имеет вид
называется единичной и имеет вид 
Обратная матрица находится по формуле:

Пример. Найти обратную матрицу к матрице 
Сначала вычисляем определитель. 
Находим алгебраические дополнения:



Записываем обратную матрицу:

Чтобы проверить вычисления, надо убедиться, что  .
.

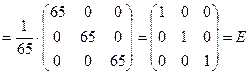
Пусть дана система линейных уравнений:

Обозначим 
Тогда система уравнений может быть записана в матричной форме как  , а отсюда
, а отсюда 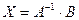 . Полученная формула называется матричным способом решения системы.
. Полученная формула называется матричным способом решения системы.
Задание 3.Решить систему матричным способом.

Надо выписать матрицу системы, найти к ней обратную и затем умножить на столбец правых частей.

Обратная матрица у нас уже найдена в предыдущем примере, значит можно находить решение:

Ответ: 
- Решение систем линейных алгебраических уравнений методом Гаусса.
Метод Крамера и матричный метод применяется только для квадратных систем (число уравнений равно числу неизвестных), причем определитель должен быть не равен нулю. Если число уравнений не равно числу неизвестных, или определитель системы равен нулю, применяется метод Гаусса. Метод Гаусса можно применять для решения любых систем.
Мы рассмотрим решение системы четвертого порядка. Если применять метод Крамера, придется находить пять определителей четвертого порядка. Если решиться обращать матрицу четвертого порядка, то придется находить 16 определителей третьего порядка.
Метод Гаусса состоит в приведении матрицы системы к треугольной или трапециевидной форме.
Пример. Решить систему третьего порядка методом Гаусса.

Выписываем матрицу системы, в которую включаем и правые части:

Матрица приведена к треугольной форме (столбец правых частей не считается). По матрице восстановим систему:

Из последнего уравнения находим  . Подставим во второе уравнение:
. Подставим во второе уравнение:
 . Найденные
. Найденные  и
и 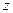 подставим в первое уравнение:
подставим в первое уравнение:
 Ответ:
Ответ: 
Задание 5.Решить систему уравнений методом Гаусса.




По полученной матрице восстанавливаем систему:

Находим решение: 
Ответ: 
|
из
5.00
|
Обсуждение в статье: Транспонирование матриц |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

