Теоретические сведения. Местные потери напора – это потери, обусловленные местными гидравлическими

Местные потери напора – это потери, обусловленные местными гидравлическими сопротивлениями, т. е. такими элементами трубопроводов, в которых вследствие изменения поперечных размеров или конфигурации происходит деформация потока.

Всякая перестройка структуры потока связана с появлением дополнительных касательных напряжений, причиной которых являются возникающие в потоке дополнительные вихреобразования.

Местные потери энергии имеют ту же физическую природу, что и потери по длине, это результат преобразования части механической энергии в тепловую за счет преодоления касательных напряжений трения.

Основные виды местных потерь напора можно условно подразделить на ряд групп, соответствующих определенным видам местных сопротивлений:

· потери, связанные с изменением поперечного сечения потока (внезапное или плавное расширение и сужение);

· потери, вызванные изменением направления потока (колена, угольники, отводы);

· потери, связанные с протеканием жидкости через арматуру различного типа (краны, вентили, задвижки, заслонки, приемные и обратные клапаны, сетки, фильтры);

· потери, связанные с разделением и слиянием потоков (тройники, крестовины).

Общим для всех видов местных сопротивлений является:

· искривление линий тока;

· изменение площади живого сечения;

· отрыв основной струи от стенок с образованием водоворотных зон;

· повышение пульсации скорости и давления.

Местные потери напора определяются по формуле Вейсбаха

 

, (7.1)

 

где z – коэффициент местного сопротивления.

Коэффициент местного сопротивления зависит в основном от формы местного сопротивления и его геометрических размеров.

Теоретически достаточно точно коэффициент местного сопротивления при турбулентном режиме движения можно определить для внезапного расширения, когда труба диаметром d₁ переходит в трубу с большим диаметром d₂ (d₂ > d₁). Струя, выходящая из первой трубы, на некоторой длине расширяется и в сечении 2–2 заполняет все поперечное сечение второй трубы (рис. 7.1).

 

 

Рис. 7.1. Внезапное расширение струи

 

Расширение струи сопровождается отрывом ее от стенок и образованием водоворотной зоны, имеющей кольцевую форму. В водоворотной зоне образуются вихри, происходит непрерывный обмен частицами жидкости между основным потоком и завихренной его частью. Основной вихрь порождает другие, более мелкие вихри, что и является причиной потерь энергии, т. е. местных потерь напора h_в.р. Обозначим давление, скорость и площадь потока в сечении 1–1 через p₁, v₁, w₁, а в сечении 2–2 – через p₂, v₂, w₂ (рис. 7.1). Будем считать, что распределение скоростей в сечениях 1–1 и 2–2 равномерное, т. е. a₁ = a₂ = 1, касательное напряжение на стенке трубы между сечениями равно нулю, давление p₁ в сечении 1–1 действует по всей площади w₂.

Запишем для данных сечений уравнение Бернулли с учетом, что z₁ =
= z₂ = 0:

. (7.2)

 

Тогда

. (7.3)

 

Согласно закону, изменение количества движения отсека жидкости между сечениями 1–1 и 2–2 равно импульсу сил, действующих на этот отсек. Проекция на ось X изменения количества движения определяется по формуле

. (7.4)

 

Исходя из ранее принятого допущения, на рассматриваемый отсек жидкости действуют только силы гидродинамического давления, проектируемые на ось X,

. (7.5)

 

Приравнивая выражения (7.4) и (7.5), получаем

 

. (7.6)

 

Разделим левую и правую часть уравнения (7.6) на и, учитывая, что , преобразуем его:

 

. (7.7)

 

Умножив и разделив правую часть уравнения (7.7) на 2, подставим ее в уравнение (7.3):

. (7.8)

 

После преобразования окончательно имеем

 

. (7.9)

 

Формула (7.9) называется формулой Борда[7]. Согласно ей потери напора при внезапном расширении равны скоростному напору потерянной скорости, так как разность (v₁ – v₂) называют потерянной скоростью.

Выражение (7.9) можно привести к другому виду. Выразим первую скорость через вторую, используя уравнение расхода:

. (7.10)

Тогда . (7.11)

Обозначив , (7.12)

 

где z_в.р – коэффициент гидравлического сопротивления при внезапном расширении потока, окончательно получим

 

. (7.13)

 

Формула (7.9) может быть преобразована в отличную от (7.11) зависимость, если выразить вторую скорость через первую:

 

. (7.14)

 

Обозначив , (7.15)

 

окончательно получим . (7.16)

 

Рассмотрим внезапное сужение, т. е. переход трубы диаметром d₁ в трубу меньшего диаметра d₂ (рис. 7.2).

При переходе из трубы бо́льшего диаметра происходит сжатие потока до w_сж, а затем наступает его расширение до w₂. Многочисленные исследования показали, что потери напора на участке сжатия (от w₁ до w_сж) пренебрежимо малы по сравнению с потерями напора на участке расширения (от w_сж до w₂). Поэтому потери напора при входном сужении могут быть найдены по формуле Борда

 

. (7.17)

 

Из уравнения неразрывности потока определим

. (7.18)

 

Используя понятие коэффициента сжатия струи , преобразуем выражение (7.17):

. (7.19)

 

Обозначив 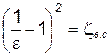, (7.20)

 

окончательно получим , (7.21)

 

где z_в.с – коэффициент местного сопротивления при внезапном расширении потока.

Коэффициент сжатия струи зависит от степени сжатия потока .

Значение z для различных видов местных сопротивлений находят экспериментально и выражают в виде эмпирических формул, графиков или в табличной форме. Причем эти значения приводятся, как правило, для скорости за местным сопротивлением.

Как показали экспериментальные исследования, коэффициент местного сопротивления зависит не только от вида самого местного сопротивления, но и от режима движения жидкости, т. е. от числа Рейнольдса. Наибольшие изменения коэффициент z от числа Re претерпевает в области ламинарного режима. При малых значениях Re жидкость протекает через местное сопротивление без отрыва, потери напора обусловлены непосредственным действием сил вязкого трения и пропорциональны скорости в первой степени. Коэффициент местного сопротивления

 

, (7.22)

 

где A – коэффициент, зависящий от вида местного сопротивления и степени стеснения потока.

При турбулентном режиме зависимость z от Re настолько незначительна, что ей можно пренебречь и считать z зависимым только от характера и конструктивного оформления местного сопротивления.

Потери напора зависят от квадрата скорости, а коэффициент местного сопротивления принимает значение z_в.с коэффициента, соответствующего квадратичной области.

Для области между ламинарным режимом и турбулентным режимом значения коэффициента местного сопротивления можно определять по формуле

. (7.23)

 

Значения A и z_кв приведены в прил. 5. Эти значения относятся к сопротивлениям, находящимся на значительном расстоянии (до 20¸40 диаметров) одно от другого. При близком расположении местных сопротивлений их необходимо рассматривать как единое сложное сопротивление.