Экономический смысл параметров уравнения линейной регрессии

Уравнение регрессии

Уравнение регрессии — это математическая формула, определяющая, каким будет среднее значение у при том или ином значении х, если все остальные факторы, влияющие на у, не учитывать, т.е. абстрагироваться от них.

Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее точно отразить зависимость между х и у, — первая задача регрессионного анализа. Виды уравнений:

1) линейная зависимость ;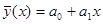

2) парабола ;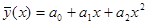

3) гипербола ;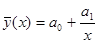

4) показательная функция ;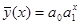

5) степенная функция 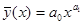и т.д.

Главным основанием для выбора типа функции должен быть содержательный анализ природы изучаемого явления. Полезно отразить зависимость графически.

 

Метод наименьших квадратов

Далее необходимо определить параметры уравнения регрессии а₀ и а₁, (для параболы еще и а₂). Для этого используют метод наименьших квадратов. В его основу положена идея минимизации суммы квадратов отклонений фактических значений у от их выравненных (теоретических) значений, т.е.

 

.

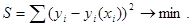где у_i — фактические значения результативного признака;

y_i(x_i) — значения у, найденные по уравнению регрессии.

Если регрессия линейная 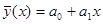, то

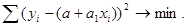
Рассматривая сумму в качестве функции параметров а₀ и а₁, определяют частные производные по а₀ и а₁ и приравнивают их к нулю, поскольку в точке экстремума производная функции равна нулю:

 

Система уравнений для разных типов зависимости между признаками

Если связь между признаками линейная, то система уравнений для нахождения параметров уравнения регрессии примет вид:

 

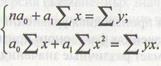
После решения системы относительно а₁ и а₁ составляют уравнение регрессии .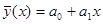

Если связь между признаками у их описывается уравнением параболы 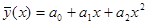, то система нормальных уравнений примет вид:

 

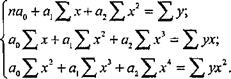
Если связь описывается уравнением гиперболы 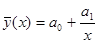, система нормальных уравнений следующая:

 

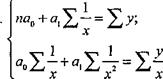
Экономический смысл параметров уравнения линейной регрессии

В уравнении линейной регрессии параметр а₀ определяет среднее значение y которое складывается под влиянием всех факторов, кроме х.

Параметр а₁ называется коэффициентом регрессии, он определяет, на сколько в среднем изменится у при изменении факторного признака на единицу. Чем больше величина а₁, тем значительнее влияние данного факторного признака на моделируемый результативный. Знак коэффициента регрессии говорит о характере влияния фактора на результативный признак.

Коэффициент эластичности показывает, на сколько процентов изменится результативный признаку при изменении факторного признака на 1%. Общая формула для расчета коэффициента эластичности выглядит следующим образом:

,

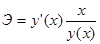где у'(х) — первая производная уравнения регрессии у(х) по х.

При различных значениях факторного признака х коэффициент эластичности принимает различные значения.

Для линейного уравнения регрессии коэффициент эластичности примет вид:

.

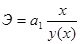Для параболической связи коэффициент эластичности равен:

.

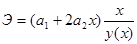Для гиперболической связи коэффициент эластичности равен:

 

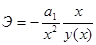
3. Корреляционный анализ. Показатели тесноты связи между признаками

В случае линейной зависимости между признаками для оценки тесноты связи применяют линейный коэффициент корреляции:

.

Линейный коэффициент корреляции изменяется в пределах от —1 до +1. Если |r|<0,3, то связь слабая. Если 0,3 <|r| < 0,7, то связь средняя. Если 0,7 < |r| < 0,9, то связь выше средней или тесная. Если |r| > 0,9, то связь сильная или весьма тесная. Если 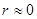, то это дает основание говорить об отсутствии линейной связи между х и у.