 |
Главная |
Явные и неявные функции
|
из
5.00
|
Определение.
Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной.
Такая функция имеет вид:  , т.е. переменная y выражается через х.
, т.е. переменная y выражается через х.
Например,  ;
; 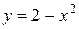 ;
;  .
.
Определение.
Неявной функцией y независимой переменной х называется функция, значения которой находятся из уравнения, связывающего х и y и, не разрешенного относительно y.
Неявная функция имеет вид:  .
.
Например,  ;
;  .
.
Замечание.
Термины «явная функция» и «неявная функция» характеризуют не природу функции, а способ ее задания.
Основные характеристики функции
Изучить функцию – это значит охарактеризовать ход ее изменения (ее поведение) при изменении независимой переменной. Характеризуют функцию по следующим свойствам:
1) четность или нечетность функции;
2) периодичность функции;
3) нули функции;
4) возрастание или убывание функции (монотонность функции);
5) ограниченность функции.
Рассмотрим эти характеристики.
Четные и нечетные функции
Определение.
Функция  называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е.
называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е.  .
.
Например,  ;
; 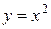 ;
;  – четные функции.
– четные функции.
График четной функции расположен симметрично относительно оси  (рис.1.4).
(рис.1.4).
 |
Рис. 1.4
Определение.
Функция  называется нечетной, если при изменении знака аргумента знак функции меняется на противоположный, а числовое значение её сохраняется, т.е.
называется нечетной, если при изменении знака аргумента знак функции меняется на противоположный, а числовое значение её сохраняется, т.е.  .
.
Например,  ;
;  – нечетные функции.
– нечетные функции.
График нечетной функции расположен симметрично относительно начала координат (рис.1.5).

Рис. 1.5
Функция может быть ни четной. ни нечетной, и в этом случае её называют функцией общего вида.
Например,  ;
;  ;
;  .
.
Графики таких функций не симметричны ни относительно оси  , ни относительно начала координат.
, ни относительно начала координат.
Периодические функции
Определение.
Функция  называется периодической, если существует такое положительное число
называется периодической, если существует такое положительное число  , что
, что  в области определения функции.
в области определения функции.
Наименьшее из положительных чисел Т, удовлетворяющих условию определения, называется периодом функции  .
.
Например, функции  ,
,  являются периодическими с периодом
являются периодическими с периодом  .
.
Нули функции
Определение.
Значение аргумента, при котором функция обращается в нуль,  , называется нулем функции.
, называется нулем функции.
Например, нулями функции 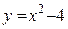 являются значения
являются значения  и
и  .
.
Монотонные функции
Определение.
Функция называется возрастающей (убывающей) в некоторой области изменения аргумента, если большему значению аргумента соответствует большее (меньшее) значение функции (рис.1.6, 1.7).
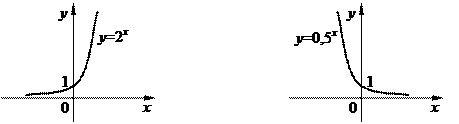 |
Рис. 1.6 Рис. 1.7
Определение.
Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной.
Ограниченные функции
Определение.
Функция  называется ограниченной на множестве Х, если существует такое число
называется ограниченной на множестве Х, если существует такое число  , что для всех
, что для всех  выполняется неравенство
выполняется неравенство  .
.
Например, функции  и
и  – ограниченные функции, т.к.
– ограниченные функции, т.к.  и
и  для
для  .
.
График ограниченной функции лежит между прямыми  и
и  (рис.1.8).
(рис.1.8).
 |
Рис. 1.8
УПРАЖНЕНИЯ
1. Найти область определения следующих функций:
1)  ; Ответ:
; Ответ:  ;
;
2)  ; Ответ:
; Ответ:  ;
;
3)  ; Ответ:
; Ответ:  ;
;
4)  ; Ответ:
; Ответ:  .
.
2. Найти множество значений функции:
1) 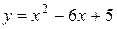 ; Ответ:
; Ответ:  ;
;
2)  ; Ответ:
; Ответ:  ;
;
3)  ; Ответ:
; Ответ:  .
.
3. Найти  ,
,  ,
,  ,
,  , если
, если  .
.
Ответ: 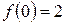 ;
;  ;
;  ;
; 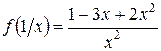 .
.
4. Пусть  и
и  . Найти
. Найти 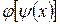 и
и  .
.
Ответ: 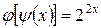 ;
;  .
.
5. Установить чётность или нечётность функции:
1)  ; Ответ: чётная;
; Ответ: чётная;
2)  ; Ответ: чётная;
; Ответ: чётная;
3)  ; Ответ: общего вида;
; Ответ: общего вида;
4)  ; Ответ: нечётная.
; Ответ: нечётная.
6. Найти основные периоды функций:
1) 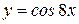 ; Ответ:
; Ответ:  ;
;
2) 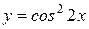 ; Ответ:
; Ответ: 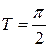 ;
;
3) 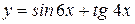 ; Ответ:
; Ответ:  .
.
7. Введя промежуточные аргументы, представить данную функцию, как суперпозицию других функций:
1) 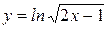 ; Ответ:
; Ответ:  ;
;  ;
; 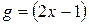 ;
;
2)  ; Ответ:
; Ответ:  ;
;  ;
; 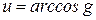 ;
;  ;
;  .
.
8. Для данных функций найти явные обратные:
1) 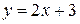 ; Ответ:
; Ответ:  ;
;
2)  ; Ответ:
; Ответ:  ;
;
3) 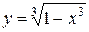 ; Ответ:
; Ответ: 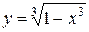 .
.
|
из
5.00
|
Обсуждение в статье: Явные и неявные функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

