Метод решения относительно одной переменной

2015-12-13

3101

Обсуждений (0)

0.00 из 5.00 0 оценок

Методы решения нелинейных уравнений и неравенств в целых числах

При решении нелинейных уравнений в целых и натуральных числах можно условно выделить следующие методы:

1. Метод разложения на множители;

2. Метод решения относительно одной переменной;

3. Метод оценки;

4. Метод остатков;

5. Метод «спуска»;

6. Метод доказательства от противного;

7. Метод параметризации уравнения;

8. Функционально-графический метод.

Метод разложения на множители

· Вынесение общих множителей за скобку.

Задание 1. Решить в целых числах уравнение 2х³+ху-7=0

Решение: Приведем уравнение к виду: х(2х²+у)=7. Так как , то рассмотрим четыре системы уравнений: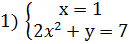

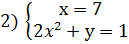
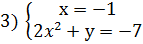
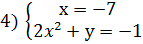
Из каждой системы получаем решения.

Ответ: (1;5); (-1;-9); (7;-97); (-7;-99)

· Применение формул сокращенного умножения.

Задание 2. Найти все пары натуральных чисел, разность квадратов которых равна 55.

Решение: Запишем условие задачи в виде уравнения n²-k²=55 или (n-k)(n+k)=55. Так как (n+k)>0, то (n-k)>0, причем (n+k)>(n-k). Поскольку , то возможны только два случая:

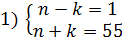
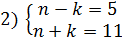. Из каждой системы получаем решения

Ответ: (28;27); (8;3)

· Способ группировки.

Задание 3. Решить в целых числах уравнение ху+3х-у=6..

Задание 3. Решить в целых числах уравнение ху+3х-у=6.

Решение: Запишем уравнение в виде х(у+3)-(у+3)=3 или (х-1)(у+3)=3. Так как , то рассмотрим четыре системы

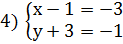
Из каждой системы получаем решения.

Ответ: (4;-2); (-2;-4); (2;0); (0;-6).

Разложение квадратного трехчлена.

Задание 4. Решить в целых числах уравнение х²-3ху+2у²=11.

Решение: решим квадратное уравнение х²-3ху+2у²=11 относительно переменной х: х₁=у и х₂=2у. Тогда получаем: (х-у)(х-2у)=11. Так как … (продолжи решение)

Ответ: (21;10); (-9;-10); (-21;-10); (9;10).

· Использование параметра.

Задание 5. Решить в целых числах уравнение 2х²-2ху++9х+у=2.

Решение: Перепишем уравнение в виде 2х²-х(2у-9)+у-2+а=аи разложим левую часть уравнения на множители как квадратный трехчлен относительно х. Найдем дискриминант D=4у²-44у+97-8а. Очевидно, если 97-8а=121, то дискриминант будет полным квадратом. При этом а=-3 и х= 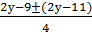. Отсюда х₁=0,5 и х₂=у-5. Уравнение принимает вид (2х-1)(х-у+5)=-3. (продолжи решение)

Ответ (1;9); (-1;3); (2;8); (0;2).

Метод решения относительно одной переменной

· Выделение целой части.

Задание 6 (МГУ, 1997). Найти все пары целых чисел х и у, удовлетворяющих уравнению 3ху+14х+17у+71=0

Решение: выразим из данного уравнения у через х: 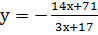. При этом следует отметить, что величина 3х+17 не равна нулю, так как х – целое число. Выделим из дроби в правой части этого равенства правильную Алгебраическую дробь (у которой степень числителя меньше степени знаменателя): . Умножим обе части последнего равенства на 3: или . Поскольку числа 3у и 14 – целые, то 3х+17 должно быть делителем числа 25, т.е. 3у+17= – всего 6 возможностей. Отсюда для х получаем три возможных значения: -4, -6, -14 (в остальных трех случаях х не является целым) Соответствующие значения у равны: -3, -13, -5.

Ответ: (-4;-3), (-6;-13), (-14;-5)

Замечание: в данном примере суть выделения целой части состоит в избавлении переменной х из числителя. В решении был использован прием домножения обеих частей равенства на коэффициент при х в знаменателе. Этот прием домножения также удобно использовать при решении уравнений методом разложения на множители.

· Использование дискриминанта (неотрицательность).

Задание 7: Решить в целых числах уравнение 3(х²+ху+у²)=х+8у

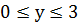Решение: Рассмотрим уравнение, как квадратное относительно х: 3(х²+ху+у²)-х-8у=0. Найдем дискриминант D=-27у²+90у+1. Данное уравнение имеет корни, если , т.е. -27у²+90у+1 . Т.к. то получаем, что . Перебирая эти значения, получаем решения уравнения.

Ответ: (0;0), (1;1)

· Использование дискриминанта (полный квадрат).

Задание 7: Решить в целых числах уравнение х²-ху+у²=х+у

Решение: Рассмотрим уравнение как квадратное относительно х: х²–(у+1)х+у²-у=0. Его дискриминант D=-3у²+6у+1=t² должен быть квадратом некоторого целого числа t. Получаем новое уравнение: 3у²-6у-1+ t²=0; 3(у-1)²+ t²=4. Из последнего уравнения следует, что t² 4, .

1. Если t²=0, то уравнение 3(у-1)²=4 не имеет целого решения у.

2. Если t²=1, то уравнение 3(у-1)²=3 имеет целые решения у₁=2 и у₂=0. При у=2 получаем квадратное уравнение х²-3х+2=0 с корнями х=1 или х=2. При у=0 получаем квадратное уравнение х²-х=0 с корнями х=0 или х=1.

3. Если t²=4, то уравнение 3(у-1)²=0 имеет одно целое решение у=1. При у=1 получаем квадратное уравнение х²-2х=0 с корнями х=0 или х=2.

Ответ: (1;2), (2;2), (0;0), (1;0), (0;1), (2;1)

Метод оценки

· Использование известных неравенств.

Задание 8: Решить в натуральных числах уравнение

Решение: Пусть для определенности . Проведем перебор для первых значений неизвестной х.

1. Если х=1, то получаем неверное равенство 1+ , так как 1+ при любых натуральных у.

2. Если х=2, то получаем неверное равенство + , так как + при любых натуральных у.

3. Если х=3, то получаем + ; , у=6.

4. Если х=4, то получаем + ; 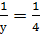, у=4.

5. Если х=5, то получаем + ; , у= 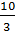- не натуральное

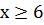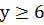6. Пусть . По условию , следовательно, . Тогда , а значит, 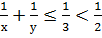. Таким образом, при исходное уравнение решений не имеет.

Заметим, что в уравнении неизвестные х и у равноправны, поэтому снимая условие имеем еще одно решение (6;3). Кроме того, можно сделать вывод, что при 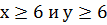исходное уравнение не имеет решений.

Ответ: (4;4), (6;3), (3;6)

Задание 9: Решить в целых числах уравнение

Решение: Можно найти вначале решения только в натуральных числах, так как если (х₀; у₀; z₀) – решение, то, изменив знак у любых двух чисел этой тройки, снова получим решение. Данное уравнение умножим на 2xyz и воспользуемся неравенством ,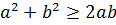

6xyz=2x²y²+2x²z²+2y²z²=(x²y²+x²z²)+(x²y²+y²z²)+(x²y²+y²z²) 2x²yz+2y²xz+2z²xy=2xyz(x+y+z), откуда x+y+z 3. Но х,у, z – натуральные, поэтому х=у= z=1 единственное решение в натуральных числах. Остальные решения в натуральных числах. Остальные решения исходного уравнения таковы: (-1; -1; 1); (1; -1; -1); (-1; 1; -1).

Ответ: (1; 1; 1); (-1; -1; 1); (1; -1; -1); (-1; 1; -1)

· Приведение к сумме неотрицательных выражений

Задание 10: Решить в целых числах уравнение х+у=х²-ху+у²

Решение: приведем уравнение к виду (х-1)²+(у-1)²+(х-у)²=2. Так как (х-1)² 2, то имеем (х-1)²=0 или (х-1)²=1. Отсюда получаем три значения х: 1, 0, 2. Подставляя эти значения в исходное уравнение, найдем значения у.

Ответ: (0,0), (1,0), (0,1), (2,1), (1,2), (2,2)

ПРОДОЛЖЕНИЕ СЛЕДУЕТ

2015-12-13

3101

Обсуждений (0)

0.00 из 5.00 0 оценок

Обсуждение в статье: Метод решения относительно одной переменной

Обсуждений еще не было, будьте первым... ↓↓↓