Температурное расширение арматуры

(1) Температурное расширение e_s(q), исходя из длины при температуре 20 °С, определяется следующим образом:

— для ненапрягаемой арматуры:

e_s(q) = –2,416 ∙ 10^–4 + 1,2 ∙ 10^–5 ∙ q + 0,4 ∙ 10^–8 ∙ q² при 20 °С £ q £ 750 °С;

e_s(q) = 11 ∙ 10^–3 при 750 °С < q £ 860 °С;

e_s(q) = –6,2 ∙ 10^–3 + 2 ∙ 10^–5 ∙ q при 860 °С < q £ 1200 °С;

— для напрягаемой арматуры:

e_s(q) = –2,016 ∙ 10^–4 + 10^–5 ∙ q + 0,4 ∙ 10^–8 ∙ q² при 20 °С £ q £ 1200 °С,

где q — температура арматуры.

(2) Зависимость температурного расширения арматуры от температуры приведена на рисунке 3.8.

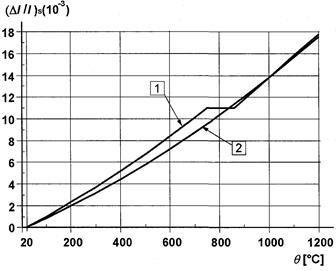
1 — ненапрягаемая арматура, 2 — напрягаемая арматура

Рисунок 3.8 — Общее температурное расширение арматуры

Методы расчета

Общие положения

(1)Р C учетом выполнения 2.4.1 (2)Р применяются следующие методы:

— конструирование согласно признанным проектным решениям (табличные данные или результаты испытаний) (раздел 5);

— упрощенные методы расчета для конструкций установленного типа (см. 4.2);

— общие методы расчета для имитации работы конструкций, частей конструктивной системы или конструктивной системы в целом (см. 4.3).

Примечание 1 — При использовании расчетных методов необходимо обеспечить целостность (Е) согласно 4.6.

Примечание 2 — При определении теплоизолирующей способности (I) начальная температура окружающей среды принимается 20 °С.

Примечание 3 — Необходимость использования общих методов расчета устанавливается в национальном приложении.

(2)Р При невозможности предотвращения хрупкого разрушения применением соответствующих проектных решений его следует учитывать в расчетах (см. 4.5).

(3) Внезапное разрушение предварительно напряженных элементов без сцепления арматуры с бетоном вследствие чрезмерного удлинения арматуры при нагреве не допускается.

Упрощенные методы расчета

Общие положения

(1) Упрощенный метод расчета сечений, нормальных к продольной оси конструкции, может использоваться для определения предельной несущей способности нагретого сечения и ее сравнения с несущей способностью для установленного сочетания воздействий (см. 2.4.2).

Примечание 1 — В приложении В приведены методы расчета несущей способности при действии изгибающих моментов и продольных усилий: В.1 «Метод изотермы 500 °С» и В.2 «Зонный метод». Методы могут включать воздействия по теории второго порядка. Метод В.1 применяется для стандартного температурного режима
и параметрического воздействия пожара, метод В.2 — только для стандартного температурного режима пожара. Метод В.2 применяется для малых сечений и гибких колонн.

Примечание 2 — В приложении С приведен «Зонный метод» для расчета сечений колонн со значительными воздействиями по теории второго порядка.

(2) Срез, кручение и анкеровка рассмотрены в 4.4.

Примечание — В приложение D приведен упрощенный метод расчета на срез, кручение и анкеровки.

(3) Для расчета балок и плит с преимущественно равномерным распределением нагрузки могут применяться упрощенные методы, если их проектирование при нормальной температуре основывается на линейном анализе (линейно-упругом методе расчета).

Примечание — В приложении Е приведен упрощенный метод расчета балок и плит.

Профили температур

(1) Температуры прогрева железобетонной конструкции при пожаре определяются расчетом или экспериментально.

Примечание — Приложение А может использоваться для определения температур в сечениях железобетонных конструкций при стандартном температурном режиме пожара в момент достижения максимальной температуры среды (газов) в помещении.

Приведенное поперечное сечение

(1) Допускается применение упрощенных методов расчета, использующих приведенное сечение, нормальное к продольной оси конструкции.

Примечание — В приложении В приведены методы, основанные на использовании приведенного бетонного сечения, нормального к продольной оси конструкции, с напрягаемой и ненапрягаемой арматурой по отношению
к продольному усилию, изгибающему моменту и их сочетанию.

Метод В.1 основан на предположении о том, что бетон, нагретый выше 500 °С, полностью теряет прочность,
и в расчетах несущей способности им пренебрегают, а бетон, нагретый ниже 500 °С, сохраняет начальную прочность без изменений.

Метод В.2 основан на принципе, что сечение при пожаре уменьшается путем исключения поврежденной зоны на подверженной воздействию пожара поверхности. Расчет производится согласно установленному алгоритму.

Снижение прочности

Общие положения

(1) В настоящем подразделе приведены зависимости нормативного сопротивления бетона сжатию, нормативного сопротивления ненапрягаемой и напрягаемой арматуры от температуры. Допускается их применять в упрощенных методах расчета (см. 4.2.3).

(2) Зависимости, приведенные в 4.2.4.2 и 4.2.4.3, применяются только для температурных режимов пожара, сравнимых со стандартным в момент достижения максимальной температуры в помещении.

(3) Допускается использовать другие законы изменения характеристик материалов, если они не противоречат экспериментальным данным.

Бетон

(1) Зависимость нормативного сопротивления бетона сжатию от температуры q(k_c(q) = f_c,q/f_ck) приведена в таблице 3.1, графа 2 — для бетона с силикатным заполнителем, графа 5 — для бетона
с карбонатным заполнителем (рисунок 4.1).

1 — бетон нормальной плотности с силикатным заполнителем;

2 — бетон нормальной плотности с карбонатным заполнителем

Рисунок 4.1 — Коэффициент снижениянормативного сопротивления бетона(k_c(q)= f_c,q /f_ck)

Арматура

(1)Для растянутой арматуры зависимость нормативного сопротивления от температуры q (k_s(q) = f_sp,q/f_yk) приведена в таблице 3.2а. Для растянутой ненапрягаемой арматуры класса N в балках и плитах с e_s,fi ³ 2 % следует применять таблицу 3.2а: графа 2 — для горячекатаной арматуры, графа 3 — для холодно­деформированной арматуры (рисунок 4.2а, кривые 1 и 2).

Зависимость нормативного сопротивления ненапрягаемой арматуры класса Х от температуры q(k_s(q) = f_sp,q/f_yk) приведена в таблице 3.2b для горячекатаной и холоднодеформированной арматуры (рисунок 4.2b, кривая 1).

В колоннах, сжатых зонах балок и плит зависимость нормативного сопротивления при 0,2 % остаточного необратимого удлинения (k_s(q) = f_sp,q/f_yk) от температуры для сжатой ненапрягаемой арматуры класса N определяется следующим образом:

k_s(q) = 1 при 20 °С £ q £ 100 °С;

k_s(q) = 0,7 – 0,3 ∙ (q – 400)/300 при 100 °С < q £ 400 °С;

k_s(θ) = 0,57 – 0,13 ∙ (q – 500)/100 при 400 °С < q £ 500 °С;

k_s(q) = 0,1 – 0,47 ∙ (q – 700)/200 при 500 °С < q £ 700 °С;

k_s(q) = 0,1 ∙ (1200 – q)/500 при 700 °С < q £ 1200 °С.

Формулы справедливы для растянутой арматуры с e_s,fi < 2 % в упрощенных методах расчета поперечного сечения (рисунок 4.2а, кривая 3).

Аналогично зависимость сопротивления при 0,2 % остаточного необратимого удлинения от температуры q (k_s(q) = f_sp,q/f_yk) для сжатой ненапрягаемой арматуры класса Х определяется следующим образом:

ks(q) = 1	при 20 °С £ q £ 100 °С;
ks(q) = 0,8 – 0,2 ∙ (q – 400)/300	при 100 °С < q £ 400 °С;
ks(q) = 0,6 – 0,2 ∙ (q – 500)/100	при 400 °С < q £ 500 °С;
ks(q) = 0,33 – 0,27 ∙ (q – 600)/100	при 500 °С < q £ 600 °С;
ks(q) = 0,15 – 0,18 ∙ (q – 700)/100	при 600 °С < q £ 700 °С;
ks(q) = 0,08 – 0,07 ∙ (q – 800)/100	при 700 °С < q £ 800 °С;
ks(q) = 0,05 – 0,03 ∙ (q – 900)/100	при 800 °С < q £ 900 °С;
ks(q) = 0,04 – 0,01 ∙ (q – 1000)/100	при 900 °С < q £ 1000 °С;
ks(q) = 0,04 ∙ (1200 – q)/200	при 1000 °С < q £ 1200 °С.

Формулы справедливы для растянутой арматуры с e_s,fi < 2 % (рисунок 4.2b, кривая 2).

(2) Зависимость нормативного сопротивления напрягаемой арматуры от температуры q (k_р(q) = f_py,q/(bf_pk) или k_р(q) = f_pp,q/(bf_pk)) определяется согласно 3.2.4 (2), с учетом данных таблицы 3.3, графа 2а или 2b — для холоднодеформированной арматуры, графа 3 — для термически упрочненной арматуры (рисунок 4.3).

1 — растянутая горячекатаная арматура при e_s,fi ³ 2 %;

2 — растянутая холоднодеформированная арматура при e_s,fi ³ 2 %;

3 — сжатая и растянутая при e_s,fi < 2 % арматура

Рисунок 4.2а — Коэффициент снижения нормативного сопротивления

растянутой и сжатой ненапрягаемой арматуры (Класс N) (k_s(q) = f_sp,q/f_yk)

1 — растянутая горячекатаная и холоднодеформированная арматура при e_s,fi ³ 2 %;
2 — растянутая и сжатая холоднодеформированная арматура при e_s,fi < 2 %

Рисунок 4.2b — Коэффициент k_s(q) снижения нормативного сопротивления

растянутой и сжатой ненапрягаемой арматуры (Класс X) (k_s(q) = f_sp,q/f_yk)

1a — холоднодеформированная напрягаемая арматура (проволока и канаты). Класс А;

1b — холоднодеформированная напрягаемая арматура (проволока и канаты). Класс В;

2 — термомеханически упрочненная напрягаемая арматура (стержни)

Рисунок 4.3 — Коэффициент снижения нормативного сопротивления напрягаемой арматуры

(k_р(q) = f_py,q/(bf_pk) или k_р(q) = f_pp,q/(bf_pk))

Общие методы расчета

Общие положения

(1) Общие методы расчета должны обеспечивать реалистический анализ конструктивных систем при пожаре. Они должны быть основаны на фундаментальных физических представлениях, приводящих к получению достоверных данных об ожидаемой работе соответствующей конструкции при пожаре.

(2)Р Схемы разрушения, которые невозможно рассчитать общими методами, необходимо предотвращать соответствующими способами.

(3) Общие методы расчета включают расчетные модели для определения:

— роста и распределения температуры в конструкциях (теплотехнический расчет);

— механической работы конструктивной системы или любой ее части (статический расчет).

(4) Общие методы расчета применяются с любыми температурными режимами при условии, что известны характеристики материалов для соответствующих диапазона температур и режима нагрева.

(5) Общие методы расчета применяются для любого поперечного сечения.